Перелік питань для самоперевірки. Цільовою функцією та лінійною системою обмежень

Рішення

Цільовою функцією та лінійною системою обмежень

Задачі нелінійного програмування з нелінійною

Область допустимих рішень таких задач завжди опукла і утворює опуклий многокутник. Проте, на відміну від лінійного програмування, за наявності нелінійної цільової функції, оптимальне рішення не завжди розташоване у вершині многокутника.

Задача 8.2. Знайти глобальні екстремуми функції за таких обмежень:

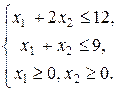
Чотирикутник 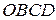є областю допустимих рішень (рис. 8.2). Лінії рівня 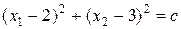є колами з центром в точці А (2;3) та радіусом .
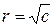З рис. 8.2 видно, що 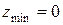і досягається в точці А, а 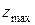досягається в
точці 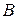. Координати точки 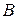є координатами точки перетину прямої 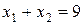з віссю 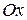, тобто 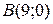і .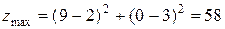

1. Постановка задачі нелінійного програмування, математична модель.

2. Графічний метод розв’язування задач нелінійного програмування.

Лекція 8

Тема 9. Динамічне програмування

Динамічне програмування (ДП) – метод оптимізації, пристосований до операцій, у яких процес прийняття рішення може бути розподілений на етапи (кроки).

Загальна постановка задачі ДП. Розглядається процес управління деякою системою S. Це може бути, наприклад, економічний процес розподілу коштів між підприємствами, використання ресурсів протягом ряду років, заміни облад-нання і таке інше. У результаті управління X система (об’єкт управління) S переводиться з початкового стану 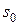в кінцевий стан 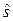. Припустимо, що управління X можна розбити на n кроків, тобто рішення приймається послідовно на кожному кроці, і являє собою сукупність n покрокових управлінь 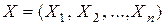. Позначаючи через 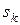стан системи після k- го кроку управління, одержуємо послідовність станів 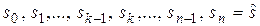(рис. 9.1).

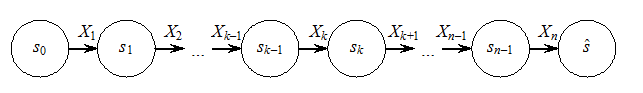Рис. 9.1

Метод динамічного програмування передбачає, що стан 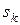системи наприкінці k- го кроку залежить тільки від попереднього стану 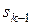і управління на k- му кроці 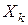(відсутність післядії), тобто

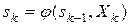, k =1, 2,…, n. (9.1)

Рівняння (9.1) називають рівняннями станів.

Показник ефективності управління Z – цільова функція задачі– є адитивним, тобто складається з показників ефективності кожного кроку. Позначимо показник ефективності k- го кроку через

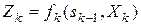, k =1, 2,…, n,

тоді

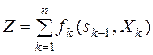. (9.2)

Задача покрокової оптимізації ДП: визначити таке допустиме управління X, що переводить систему S зі стану 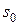в стан 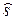, при якому цільова функція (9.2) набуває найбільшого (найменшого) значення.

Метод розв’язання задачі ДП базується на принципі оптимальності (Беллмана): Яким би не був стан s системи в результаті якого-небудь числа кроків, на найближчому кроці потрібно вибирати управління так, щоб воно в сукупності з оптимальним управлінням на всіх наступних кроках приводило до оптимального виграшу на всіх кроках, що залишилися, включаючи даний.

Формальним виразом цього принципу є рівняння Беллмана. У задачі максимізації цільової функції вони мають вид:

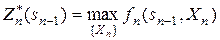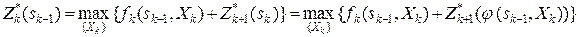, , k = n –1, n –2, …, 2, 1.

(9.3)

Величина 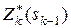називається умовним максимумом цільової функції, що одержується при оптимальному управлінні на n – k +1 кроках, починаючи з k-го до кінця, за умови, що напередодні k-го кроку система перебувала в стані 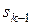. Управління 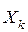на k -му кроці, при якому досягається 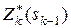, позначається через і називається умовним оптимальним управлінням на k-му кроці, k = n, n –1, …, 1.

Схема застосування методу ДП

1. Вибирають спосіб розподілу процесу управління на кроки.

2. Визначають параметри стану 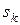і змінні управління 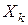на кожному кроці.

3. Записують рівняння станів.

4. Вводять цільові функції k- го кроку і сумарну цільову функцію.

5. Вводять у розгляд умовні максимуми (мінімуми) 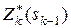і умовне оптимальне управління на k- му кроці: , k = n, n –1, …, 1.

6. Записують рівняння Беллмана для 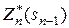і 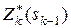, k = n –1, …, 1.

7. Розв’язують послідовно рівняння Беллмана (умовна оптимізація) і одержують дві послідовності функцій: { 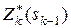} і { }.

8. Знаходять оптимальне рішення для конкретного початкового стану :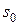

а) ;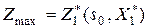

б) .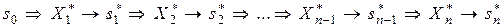

(Стрілка 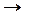означає використання рівнянь стану, а стрілка 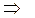– послідовності умовних оптимальних управлінь через розв’язок рівнянь Беллмана);

в) оптимальне управління: .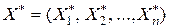

9.1. Задача про розподіл коштів між підприємствами

Задача 9.1. Планується діяльність чотирьох промислових підприємств на черговий рік. Початкові кошти: 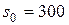тис. грош. од. Кошти x, виділені k- му підприємству (k =1,2,3,4), приносять наприкінці року прибуток 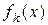. Функції 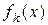задані таблично (табл. 9.1). Визначити, скільки коштів потрібно виділити кожному підприємству, щоб сумарний прибуток був найбільшим.

	Таблиця 9.1
x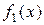

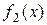
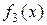
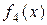
Дата добавления: 2014-11-06