МАТЕМАТИКА 1 страница

Методические указания к изучению дисциплины

и выполнению контрольной работы

для студентов заочной формы обучения СПО

Санкт – Петербург

Допущено

редакционно-издательским советом СПбГИЭУ

в качестве методического издания

Составители

канд. техн. наук, доц. Я.В.Войтишек

ст. преп. Н.А.Полозенко

Рецензент

д. ф-м. н., профессор И.Е. Погодин

Подготовлено на кафедре высшей математики

Одобрено научно-методическим советом университета

Отпечатано в авторской редакции с оригинал-макета,

представленного составителями

Содержание

Стр.

1. Общие положения………………………………………...4

2. Методические указания к изучению дисциплины……...5

3. Методические указания к выполнению контрольной

Работы……………………………………………………..5

Тема 1. Иррациональные уравнения…………………….5

Тема 2. Иррациональные неравенства…………………..8

Тема 3. Показательные уравнения……………………....9

Тема 4. Логарифмические уравнения………………….10

Тема 5. Логарифмические и показательные

неравенства……………………………………..13

Тема 6. Тригонометрические уравнения……………....16

Тема 7. Производная………………………………….....20

4. Контрольные задания…………………………………...22

5. Требования к оформлению контрольной работы……..31

6. Рекомендуемая литература……………………………..31

Приложение 1. Содержание дисциплины (Извлечение

из рабочей программы дисциплины)…....33

Приложение 2. Перечень контрольных вопросов для

проверки знаний по дисциплине..............35

Приложение 3. Образец оформления титульного листа

контрольной работы……………………..37

1. Общие положения

Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей:

· формирование представлений о математике как универ-

сальном языке науки, средстве моделирования явлений и процес-

сов, об идеях и методах математики;

· развитие логического мышления, пространственного во-

ображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности.

· овладение математическими знаниями и умениями, необ-

ходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующей углублённой математичес-

кой подготовки.

· воспитание средствами математики культуры личности,

отношения к математике как части общечеловеческой культуры.

2. Методические указания к изучению дисциплины

Методические указания содержат краткое изложение теоретического материала, необходимого для выполнения контрольной работы за курс средней школы, а также содержат большое количество примеров и подробное решение типовых задач, аналогичных контрольным заданиям. Методические указания могут быть использованы студентами заочной формы обучения при выполнении контрольных работ, а также при подготовке к экзамену и зачёту.

3. Методические указания к выполнению контрольной работы

Выполнение контрольной работы служит решению задачи получения студентами необходимых практических навыков по решению задач из курса математики. Прежде чем приступить к их выполнению, необходимо внимательно изучить соответствующие разделы методических указаний.

Номер варианта контрольной работы определяется по номеру зачётной книжки и равен остатку от деления номера зачётной книжки на 20. Например, если номер 1723, то вариант контрольной работы номер 3, и следует выполнять задания 1.3; 2.3; 3.3; 4.3 и т д. Те, у кого номера зачёток кратны 20, решают вариант 20.

I. Иррациональные уравнения.

Иррациональным называют уравнение, содержащее переменную под знаком корня.

Иррациональные уравнения обычно решают на множестве действительных чисел. Решение иррациональных уравнений осуществляется, в основном, двумя способами: либо возведением обеих частей уравнения в нужную степень, либо методом введения нового неизвестного. На практике обычно приходится комбинировать оба этих способа.

Следует помнить, что при решении иррациональных уравнений необходима проверка всех найденных корней путём их подстановки в исходное уравнение или нахождения ОДЗ и последующего анализа корней. Необходимость проверки корней отпадает, если для решения иррациональных уравнений применить следующие теоремы.

Теорема 1. Для любого чётного числа 2m (m N) уравнение
равносильно системе

Теорема 2. Для любого четного числа 2m (m N) уравнение
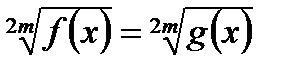равносильно системе

или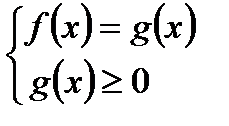

Пример 1. 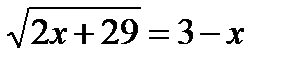. Этоуравнение равносильно системе

.
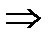
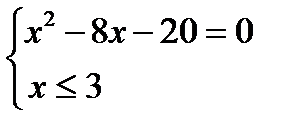Решив квадратное уравнение, найдём два корня х ₁ = –2, х ₂ = 10,
х ₂ – посторонний корень. Ответ: x = –2.

Пример 2. 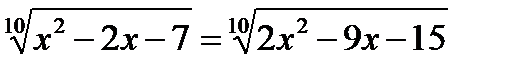. Данное уравнение равносильно системе

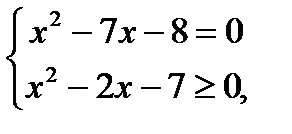
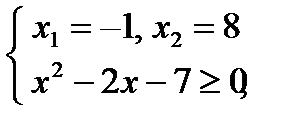х ₁ не удовлетворяет неравенству системы, следовательно, данное уравнение имеет единственное решение.

Ответ: х = 8

Пример 3. 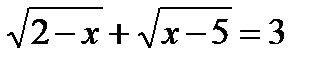. Функция 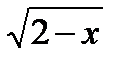определена при 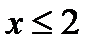, а функция определена при , но эти условия противоречивы, следовательно, данное уравнение не имеет решения Ответ:

Пример 4.

ОДЗ: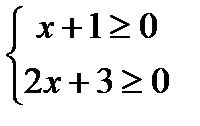

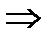
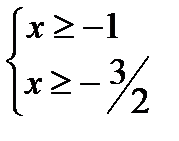
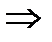
Уединим корень тогда получим уравнение

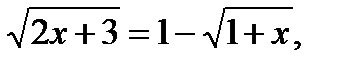это уравнение равносильно системе

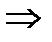
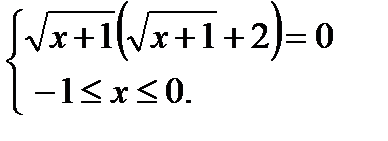
так как тогда 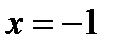. Ответ:

Пример 5. 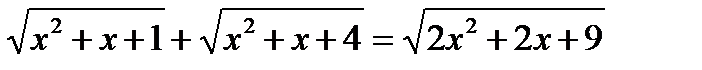. Сделаем замену 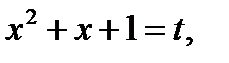тогда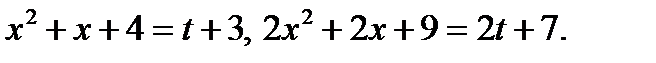

В результате получим уравнение где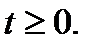

Возведём обе части уравнения в квадрат

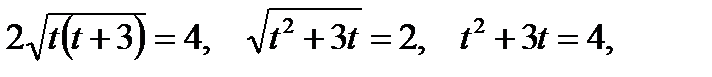
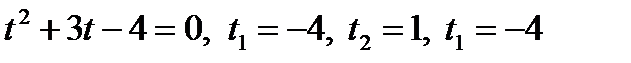не удовлетворяет ограничению.

Возвращаясь к переменной x, имеем

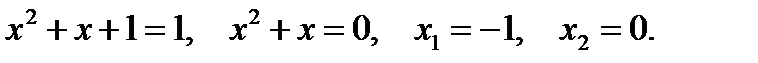Ответ:

Пример 6. . ОДЗ: .

Обозначим 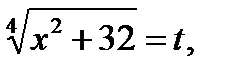где Получим уравнение

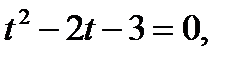корни которого равны 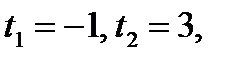так как

не удовлетворяет ограничению, то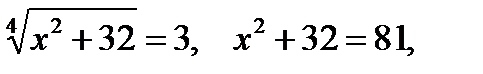

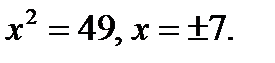Ответ: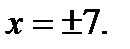

Пример 7. ОДЗ:

Обозначим 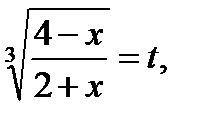тогда получим уравнение

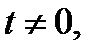
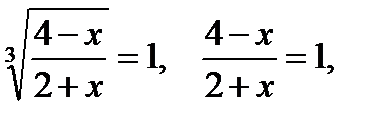
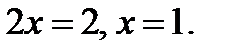Ответ: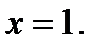

Пример 8.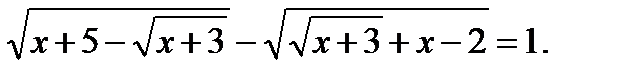

Обозначим 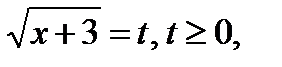тогда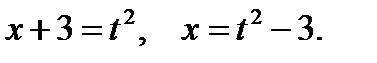

Подставим вместо x выражение 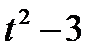в исходное уравнение, получим 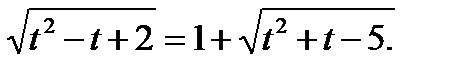Возведём обе части уравнения в

квадрат.

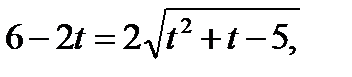
Это уравнение равносильно системе:

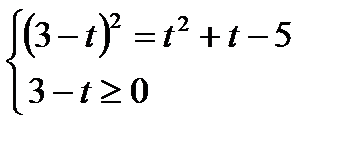
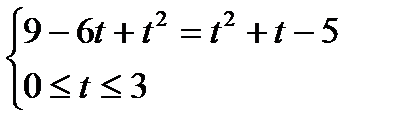, . Возвращаясь к переменной x, имеем Ответ:

II Иррациональные неравенства.

Решение иррациональных неравенств основано на следующих основных теоремах:

Теорема 1. Для любого n N неравенство

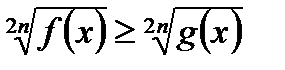
равносильно системе

Теорема 2. При любом n 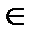N неравенство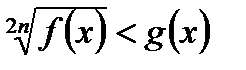

равносильно системе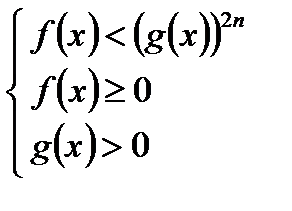

Теорема 3. Неравенство равносильно

совокупности двух систем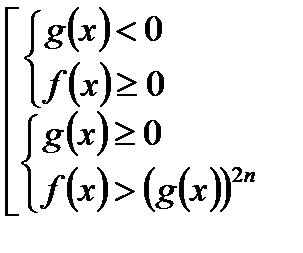

Пример 1. 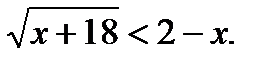По теореме (2) получаем равносильную систему

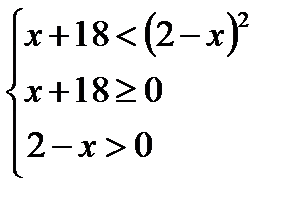
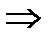
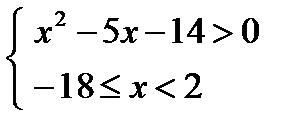
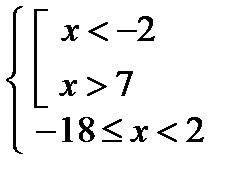Ответ:

Пример 2. 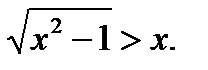По теореме (3) это неравенство равносильно совокупности двух систем неравенств

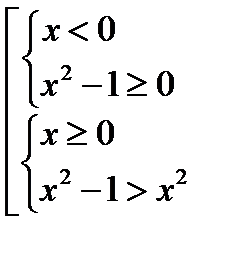
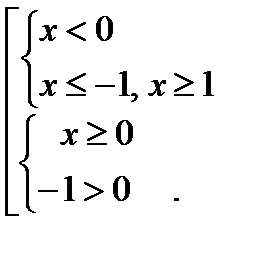
Вторая система не имеет решения. Ответ: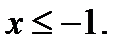

III Показательные уравнения.

Показательным уравнением называется уравнение, в котором неизвестное входит только в показатель степени. При решении показательных уравнений наиболее часто применяются следующие методы: 1) приведение обеих частей уравнения к одному основанию; 2) вынесение за скобку общего множителя; 3) введение нового неизвестного; 4) логарифмирование обеих частей уравнения.

Пример 1. 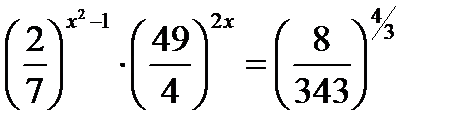Приведём все степени к основанию : , ,

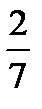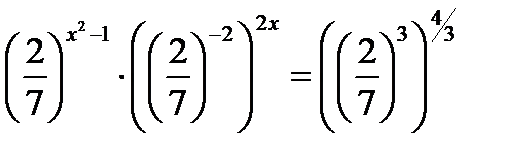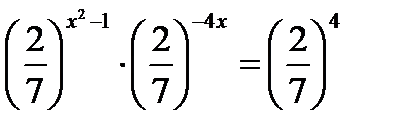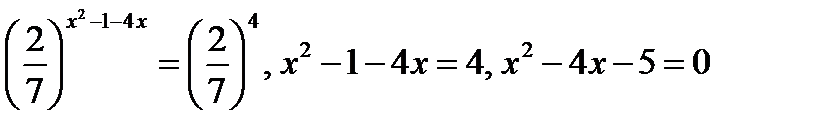
Решив это квадратное уравнение, найдём его корни

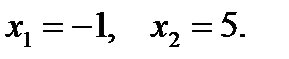Ответ: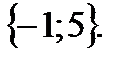

Пример 2. Вынесем в левой части уравнения множитель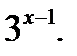

Ответ:

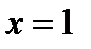
Пример 3. ОДЗ:

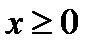
Обозначим 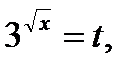где получим уравнение

Решив это квадратное уравнение, получим 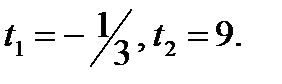t ₁ не удовлетворяет ограни-­

чению. 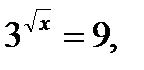Ответ:

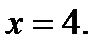
Пример 4. 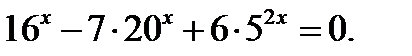Представим уравнение в виде Разделим обе части уравнения на .

Обозначим 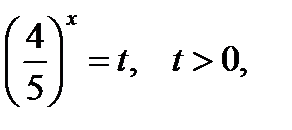приходим к квадратному уравнению корни которого

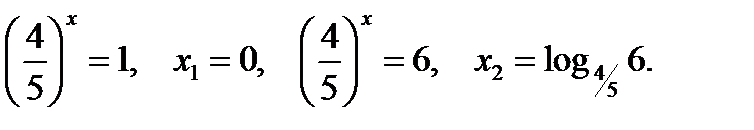Ответ: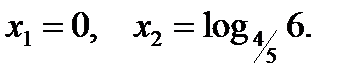

Пример 5. 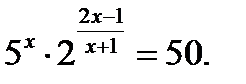ОДЗ: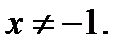

Логарифмируя обе части по основанию 2,получим уравнение

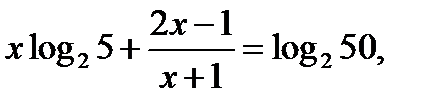умножим обе части уравнения на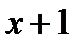

.

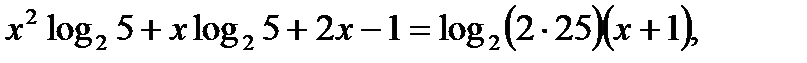
Найдём корни этого квадратного уравнения

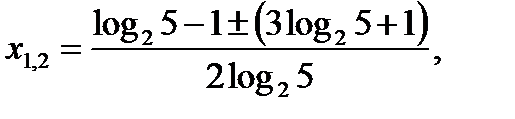
Ответ: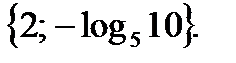

IV. Логарифмические уравнения

Логарифмом положительного числа b по основанию a (a > 0,
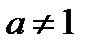) называется показатель степени х, в которую нужно возвести a, чтобы получить b, т.е.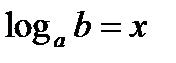 (1).

Равенство (1), выражающее определение логарифма, можно переписать в виде 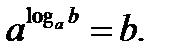(2) Это равенство называют основным логарифмическим тождеством.

Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут lg b вместо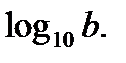

Натуральным логарифмом числа называют логарифм этого числа по основанию е, где е – иррациональное число, приближённо равное 2,71. При этом пишут ln b, вместо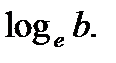

Свойства логарифмов.

1)

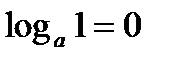
2)

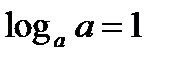
3)

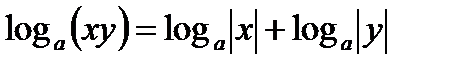
4)

5)

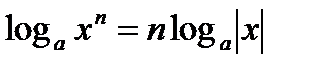
6)

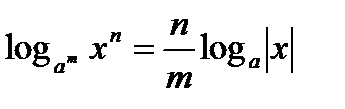
7) – это свойство называют формулой перехода от одного основания к другому.

Логарифмическим уравнением называется уравнение, содержащее неизвестное под знаком логарифма или в основании логарифма,или и то и другое одновременно.

Теорема. Уравнение 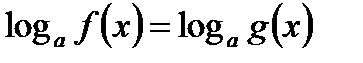равносильно системе или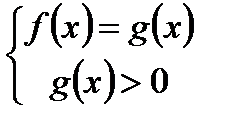

При решении логарифмических уравнений наиболее часто применяются следующие методы: 1) решение уравнений, основанное на определении логарифма; 2) решение с помощью потенцирования; 3) применение основного логарифмического тождества; 4) использование логарифмирования; 5) введение нового

неизвестного; 6) переход к логарифму по новому основанию.

Пример 1. 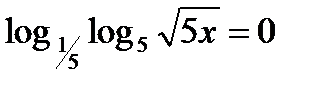. Используя определение логарифма, имеем 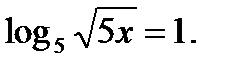Применим ещё раз определение логарифма, получаем Ответ: х = 5.

Пример 2. 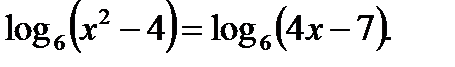Это уравнение равносильно системе . Корни квадратного уравнения равны 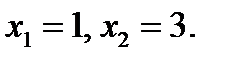не удовлетворяет неравенству системы. Ответ: х = 3.

Пример 3.

ОДЗ: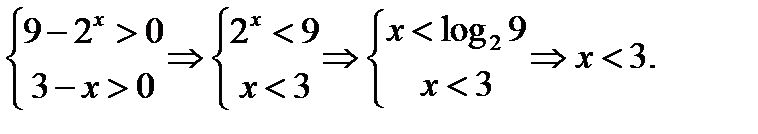

Применив к правой части уравнения основное логарифмическое тождество, получим Используя определение логарифма, имеем 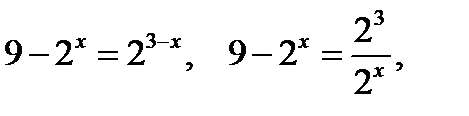обозначим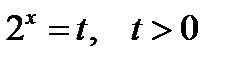

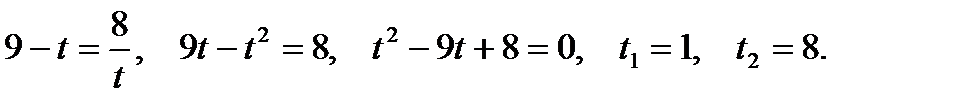
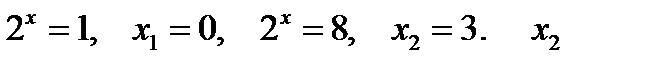не удовлетворяет ОДЗ.

Ответ: х = 0.

Пример 4. ОДЗ: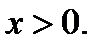

Выражения, содержащиеся в обеих частях уравнения, положительны, поэтому возможно логарифмирование, причём наиболее удобное основание 10. Имеем 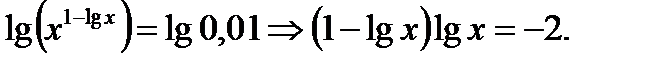Положив получаем квадратное уравнение корни которого равны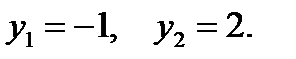

Ответ:

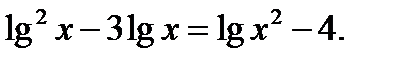Пример 5. ОДЗ: 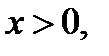поэтому

.Получаем квадратное уравнение 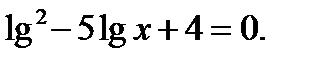Обозначим

Ответ:

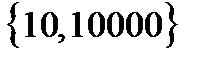
Пример 6.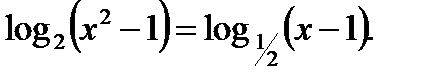

ОДЗ: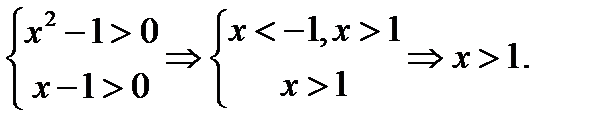

Перейдём к основанию 2 в правой части уравнения.

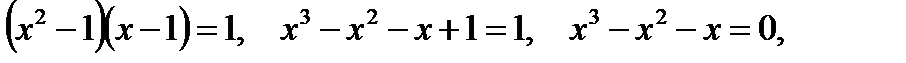
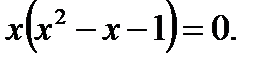
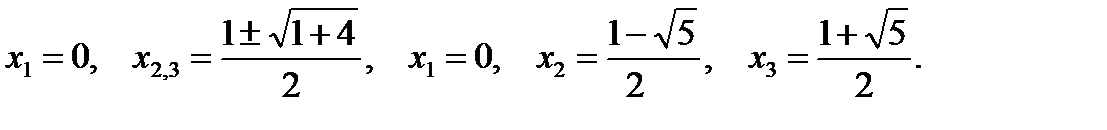
и

Не удовлетворяют ОДЗ. Ответ:

Пример 7.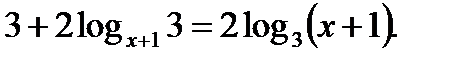

ОДЗ: Перейдём в уравнении к логарифму по основанию 3. 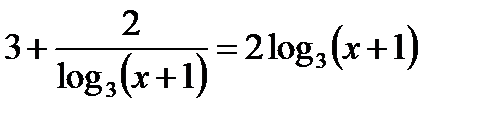. Пусть

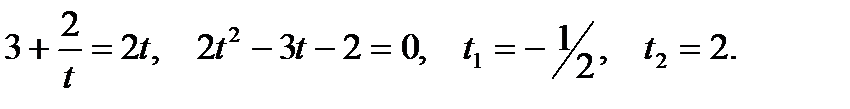
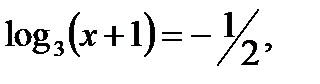
Ответ:

V. Показательные и логарифмические неравенства

Решение показательных и логарифмических неравенств основано на монотонности показательной и логарифмической функций.

Как известно, при 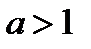обе функции возрастают, а при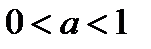

обе убывают.

Теорема 1. Неравенство 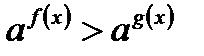равносильно неравенству при а при

Теорема 2. Неравенство 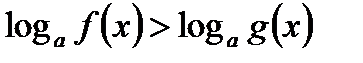равносильно системе при ,. при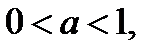

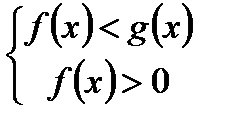
Дата добавления: 2014-11-06