МАТЕМАТИКА 2 страница

Пример 1.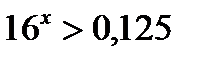

Ответ:

Пример 2. 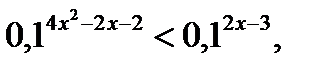так как 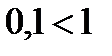, по теореме 1 получаем неравенство

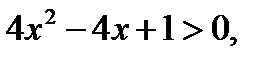
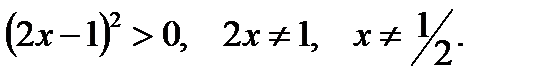Ответ:

Пример 3.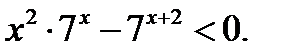

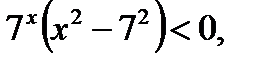так как при всех 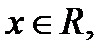то неравенство равносильно следующему неравенству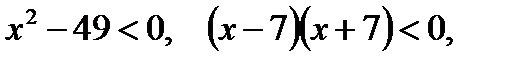

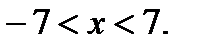Ответ: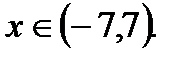

Пример 4. 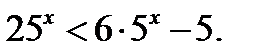Пусть . Получаем квадратное неравенство Корни квадратного трёхчлена равны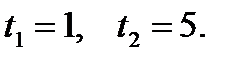

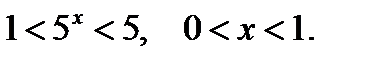Ответ:

Пример 5. ОДЗ:

Пусть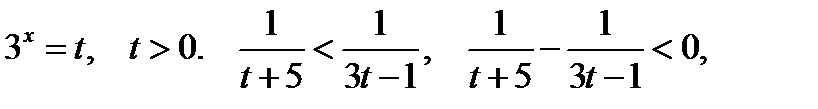

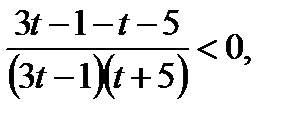
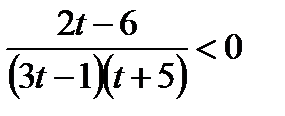. Решая это неравенство методом интервалов, с учётом ограничения, получим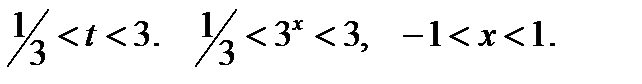

Ответ: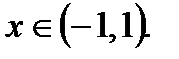

Пример 6. 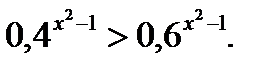Разделим обе части неравенства на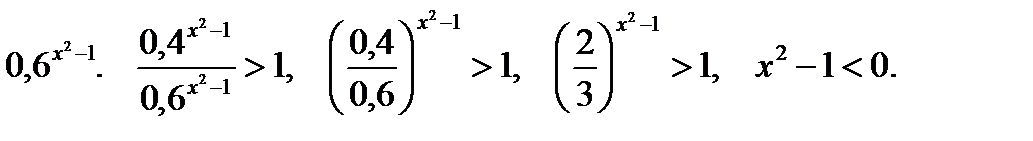

Ответ:

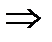
Пример 7. Это неравенство равносильно системе: . Решением первого неравенства являются все 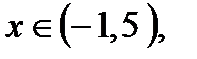а решением второго неравенства являются все 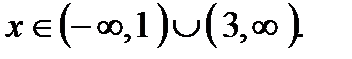тому и другому неравенству удовлетворяют

Ответ: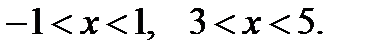

Пример 8. Данное неравенство равносильно системе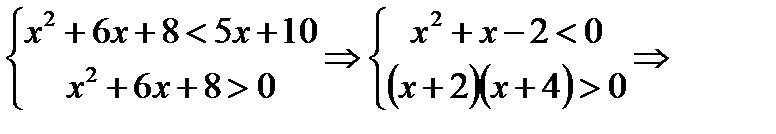

. Ответ: .

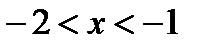Пример 9. 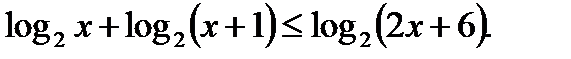ОДЗ:

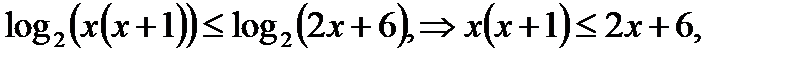
, решая

это неравенство, имеем 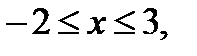учитывая ОДЗ, получаем

Ответ: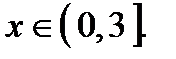

Пример 10.

Решая это неравенство методом интервалов, получаем

Ответ:

Пример 11. Если в неравенстве встречается логарифмическая функция, содержащая неизвестное в основании, то, как правило, следует рассматривать два случая: 1) основание больше 1 и 2) основание положительно, но меньше 1.

1) 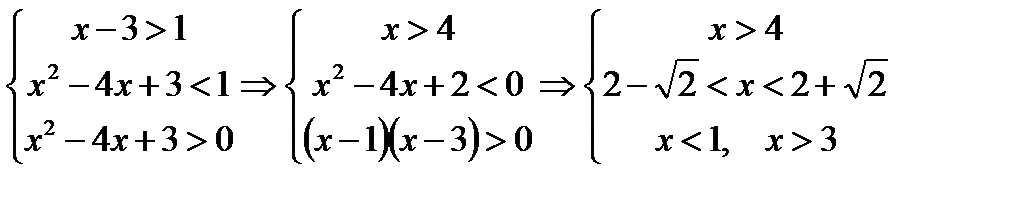, первое и второе неравенство не имеют общих точек, система 1) не имеет решений.

2)

○ ○ ○ ○ Ответ: .

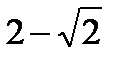
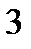
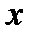
VI. Тригонометрические уравнения

Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.

Простейшими тригонометрическими уравнениями являются уравнения вида Напомним общие формулы решения простейших тригонометрических уравнений: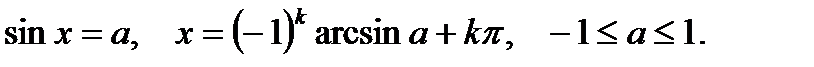

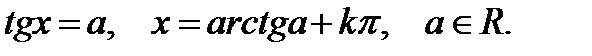
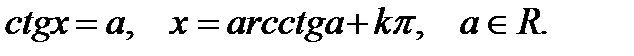
Во всех приведённых формулах Значения обратных тригонометрических функций берутся из следующих промежутков:

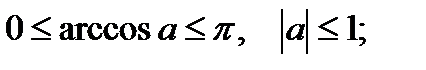
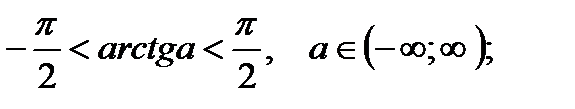
Любое тригонометрическое уравнение в процессе решения с помощью надлежащих преобразований должно быть приведено к простейшим. Наиболее часто при решении тригонометрических уравнений применяются следующие методы: 1) разложение на множители; 2) способ замены; 3) сведение к уравнениям, однородным относительно и ; 4) преобразование суммы тригонометрических функций в произведение; 5) преобразование произведения тригонометрических функций в сумму; 6) использование формул понижения степени; 7) введение вспомогательного аргумента.

При этом, как правило, в процессе решения тригонометрического уравнения приходится использовать не один, а несколько из указанных выше методов.

Пример 1.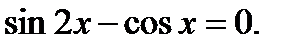

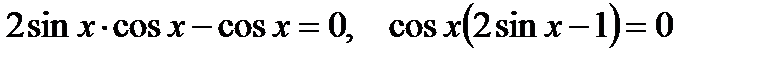. Полученное уравнение равносильно совокупности уравнений: Решение первого уравнения: Второе уравнение

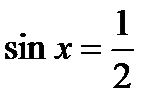, его решение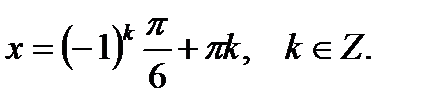

Ответ: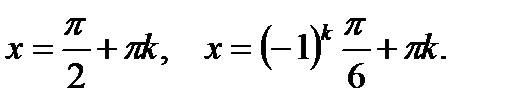

Пример 2.

Перенесём все члены уравнения в левую часть и разложим её на множители:

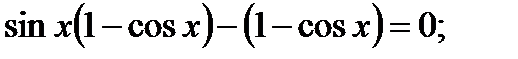
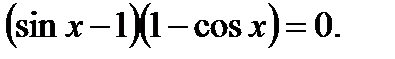Отсюда следует 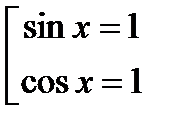Решая их, получим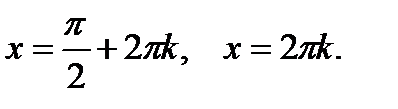

Ответ: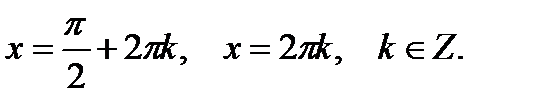

Пример 3.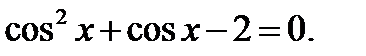

Это уравнение является квадратным относительно Поэтому сделаем замену Получим квадратное уравнение

Его корни равны 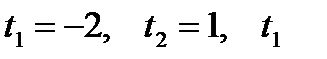не удовлетворяет

условию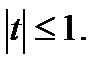

В итоге получаем Ответ:

Пример 4. 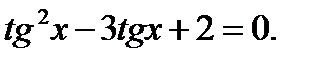ОДЗ: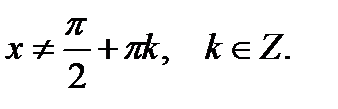

Обозначим 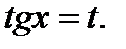Получим квадратное уравнение, корни которого равны В результате получаем два простейших тригонометрических уравнения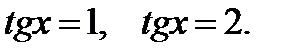

Ответ:

Решение однородных уравнений и уравнений, сводящихся к н им.

Уравнения

(1)

........................................................

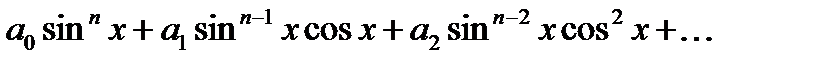
называются однородными относительно и 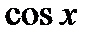. Они обладают тем свойством, что сумма показателей степеней при и у всех членов уравнения одинакова. Делением на соответственно уравнения (1) приводятся к алгебраическим уравнениям относительно 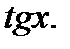При этом, конечно, предполагается, что В результате получаем равносильное уравнение, так как разделили на

(если бы 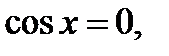то из исходного уравнения следует, что и 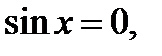а это невозможно, так как и при одном и том же значении х в нуль не обращаются, ибо всегда

).

Уравнение легко сводится к однородному, если правую часть представить в виде

После преобразований получаем

Пример 5.

Разделим обе части уравнения на получим уравнение Введём новую переменную 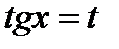и решим квадратное уравнение Его корни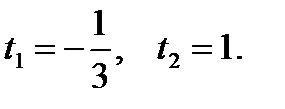

Получили два простейших тригонометрических уравнения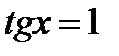

или 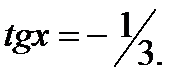Решая их получим или

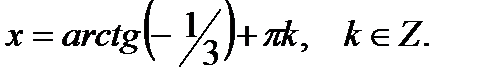Ответ:

Пример 6. Найти сумму корней уравнения

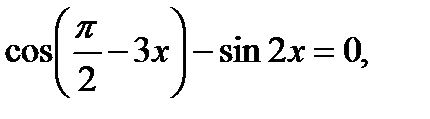если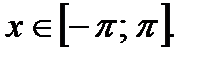

По формулам приведения 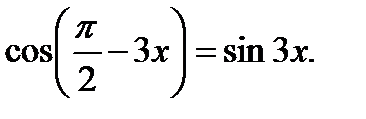Получаем уравнение

откуда 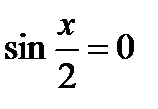или

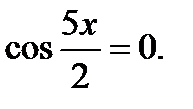
Решая эти уравнения, получим

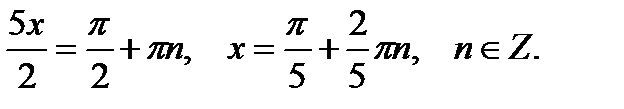Выберем те значения х, которые попадают в указанный интервал. Из первой серии корней только

при k =0 принадлежит указанному интервалу. Из второго множества корней в указанный интервал попадают:

при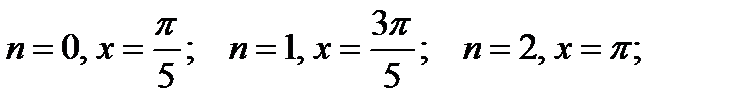

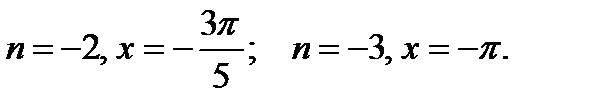Сумма всех этих корней равна 0.

Ответ: 0.

Пример 7. Найти сумму корней уравнения

если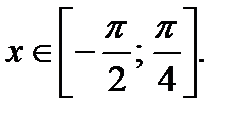

Задача свелась к решению совокупности уравнений:

или Из этих уравнений находим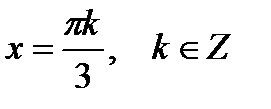

или В указанный интервал попадут следующие значения х: Сумма всех этих корней равна Ответ: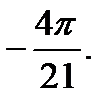

VII. Производная

Пусть на интервале 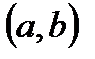задана функция

Возьмём некоторое число 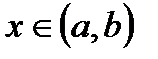и придадим аргументу х приращение Тогда значение функции получит приращение

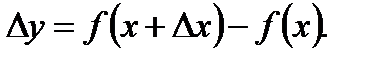Рассмотрим отношение

Если при 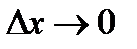существует конечный предел дроби 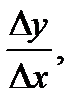то

этот предел называют производной функции в точке х и обозначают символом или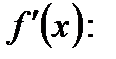

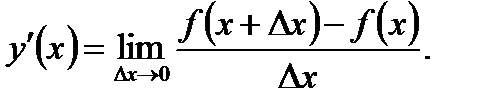
Нахождение производной называют дифференцированием функции.

Для освоения техники дифференцирования необходимо знать правила дифференцирования и таблицу производных функций.

Основные правила дифференцирования:

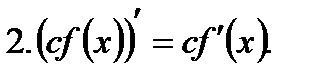
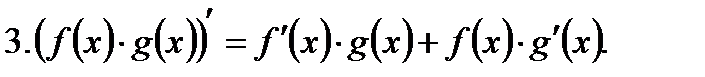
Производная сложной функции. Функция вида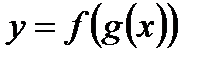

называется сложной, её производная равна

Таблица производных.

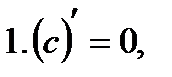где с – постоянная.

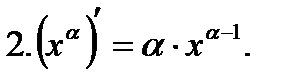
где

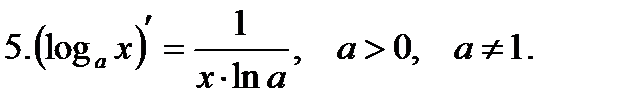
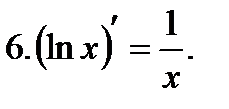
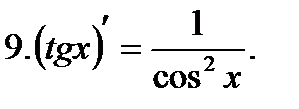
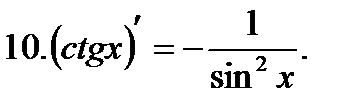
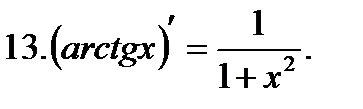
Пример 1.

Применяя правило 4 и таблицу производных, получим:

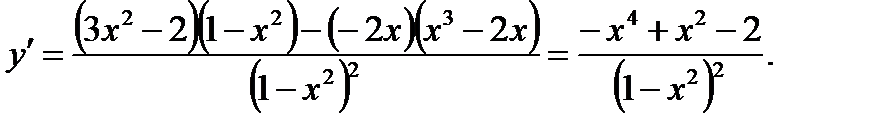
Пример 2.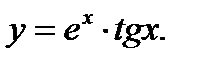

Применяяправило3 и таблицу производных, получим:

Пример 3.

Применяя правило дифференцирования сложной функции, имеем:

Пример 4. Найти значение производной функции

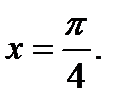
в точке

Найдём производную сложной функции, а затем вычислим её значение при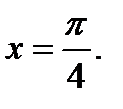

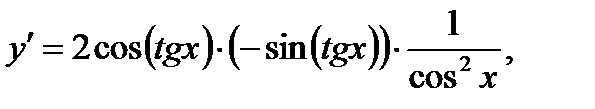
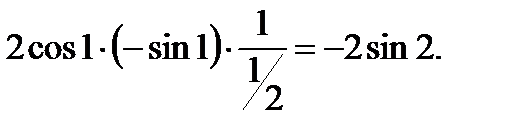
4. Задания для контрольной работы

I. Решить уравнение.

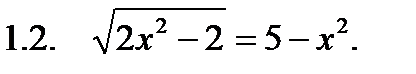
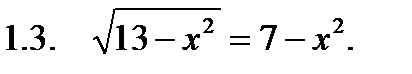
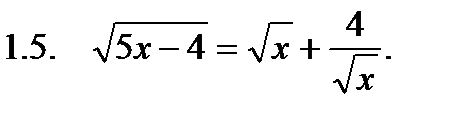
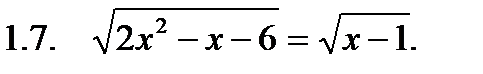
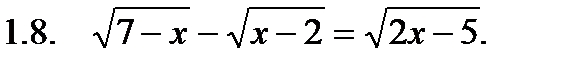
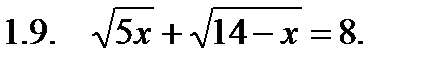
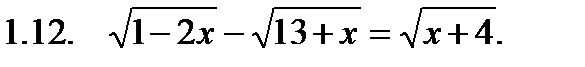
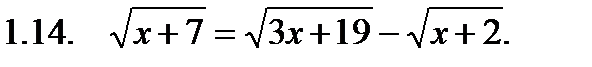
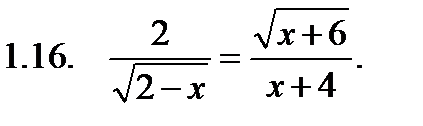
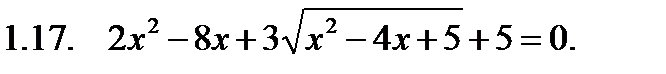
II. Решить неравенство.

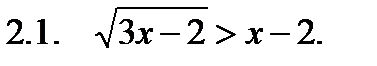
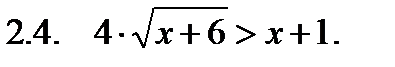
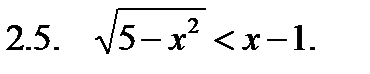
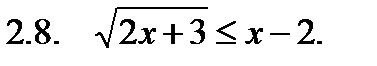
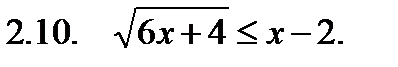
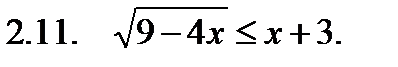
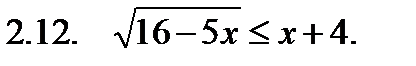
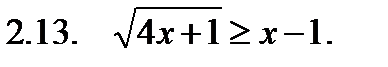
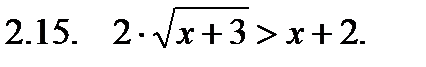
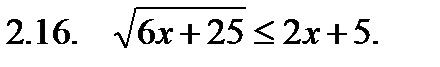
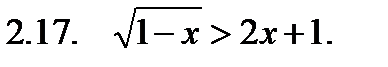
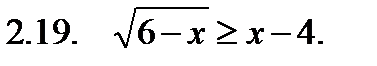
III. Решить уравнение.

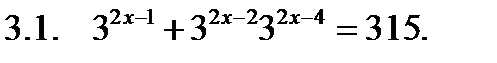
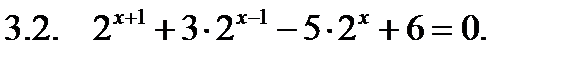
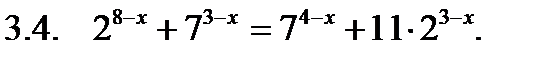
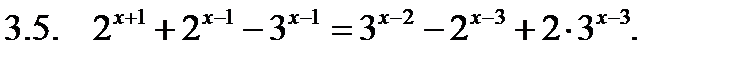
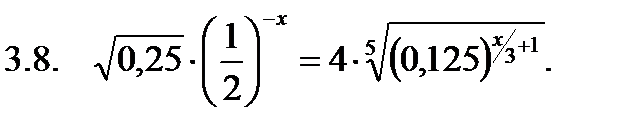
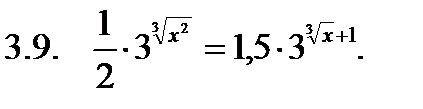
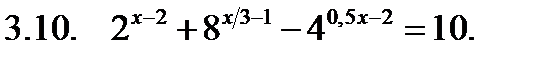
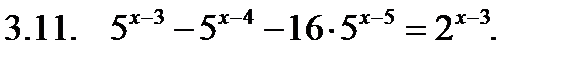
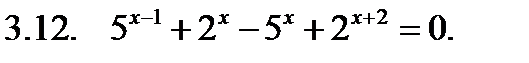
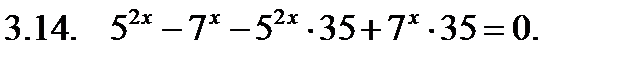
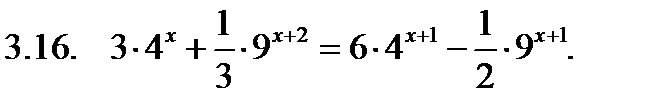
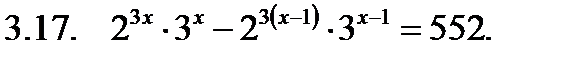
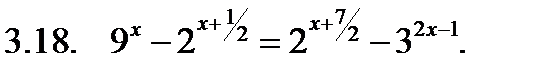
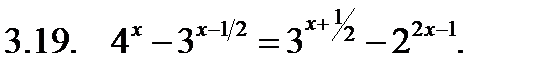
Решить уравнение.

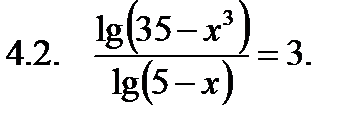
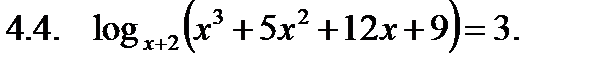
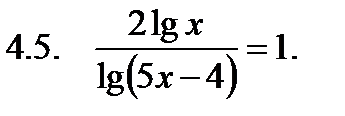
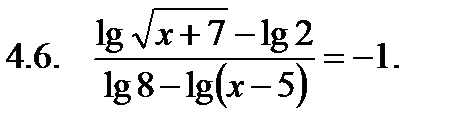
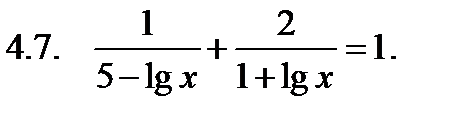
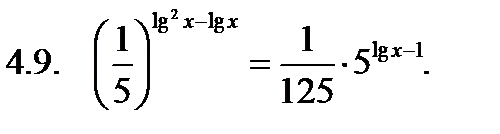
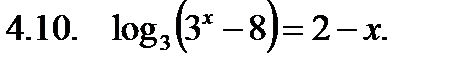
Дата добавления: 2014-11-06