МАТЕМАТИКА 3 страница

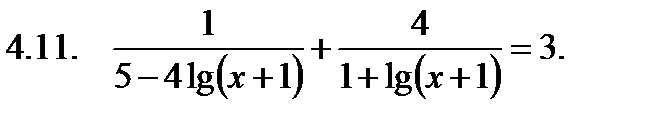
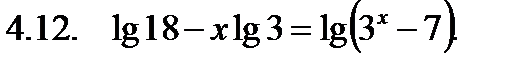
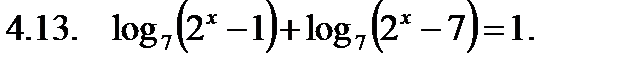
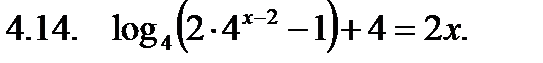
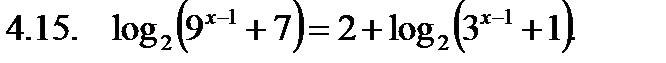
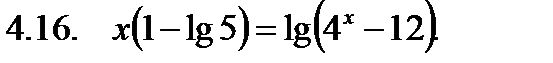
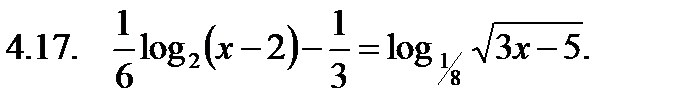
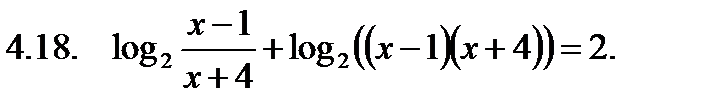
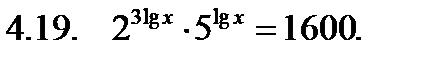
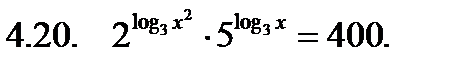
Решить неравенство.

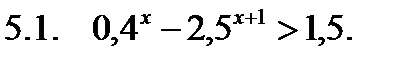
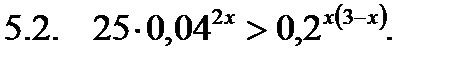
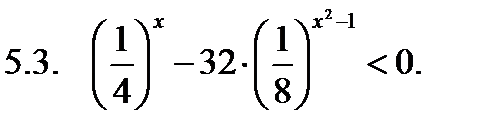
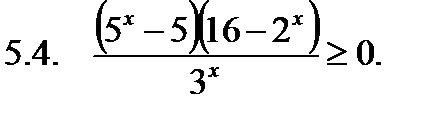
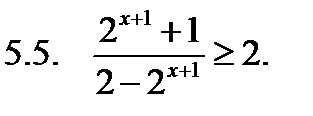
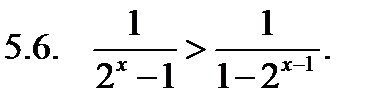
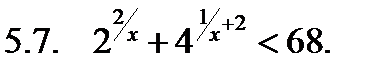
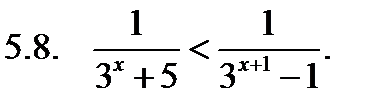
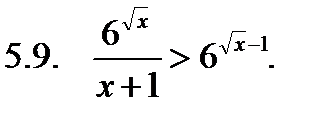
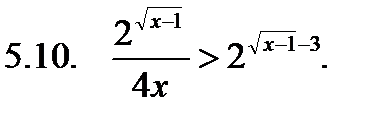
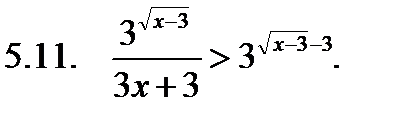
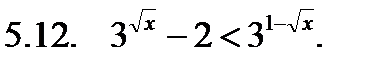
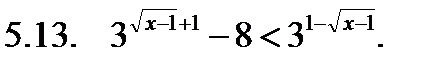
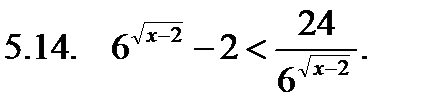
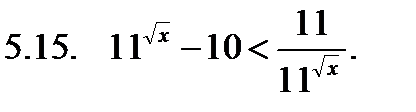
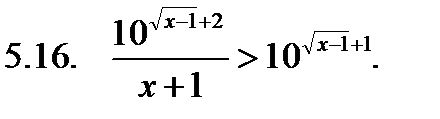
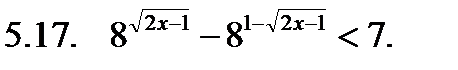
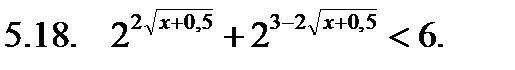
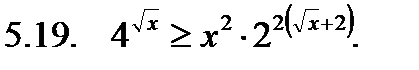
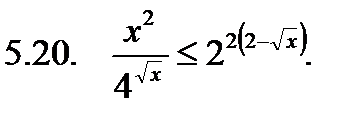
Решить неравенство.

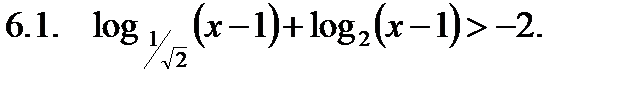
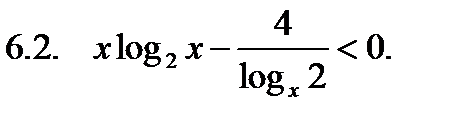
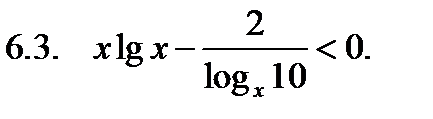
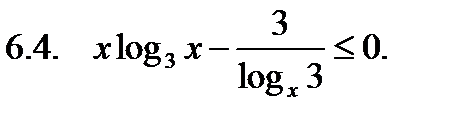
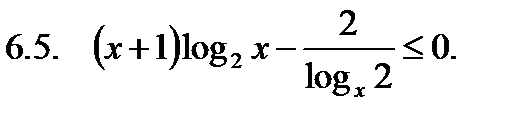
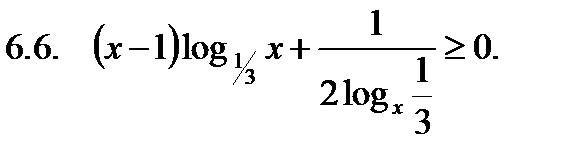
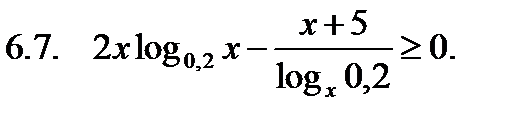
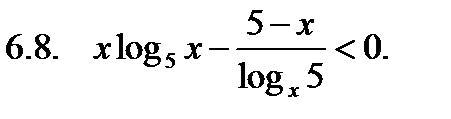
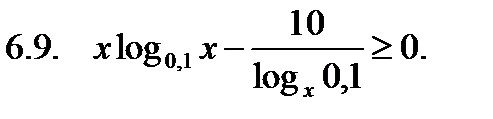
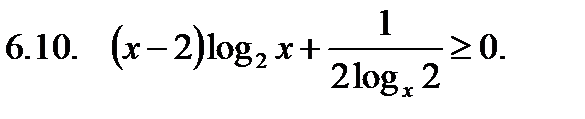
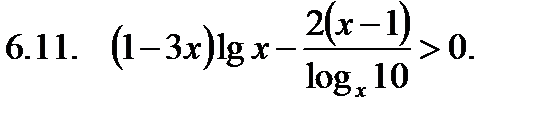
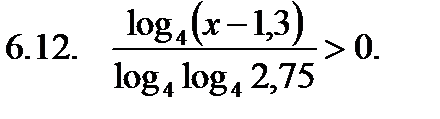
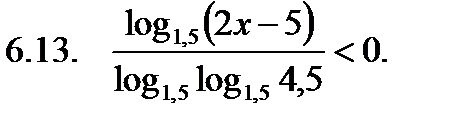
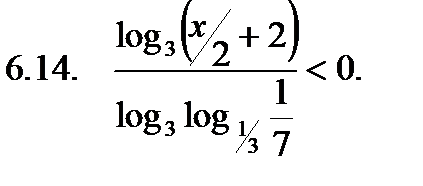
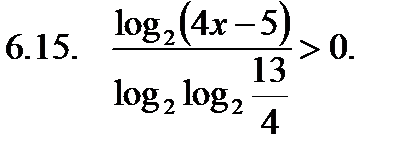
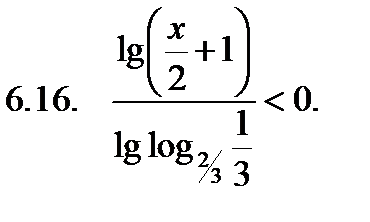
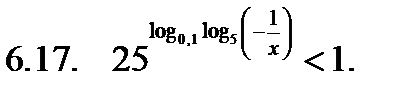
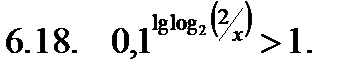
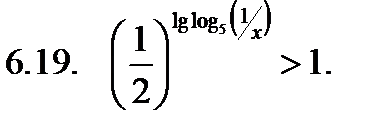
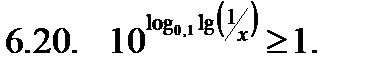
Найти сумму корней уравнения на указанном отрезке.

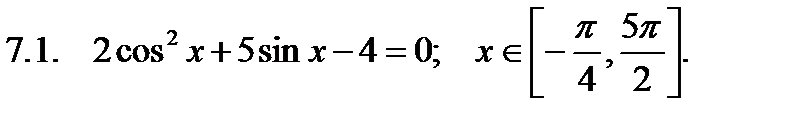
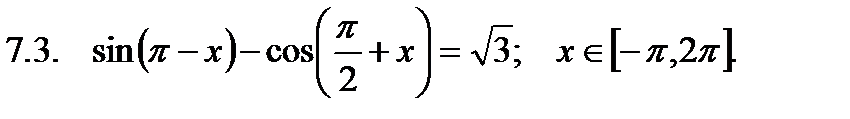
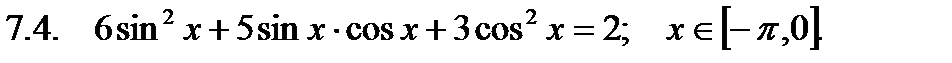
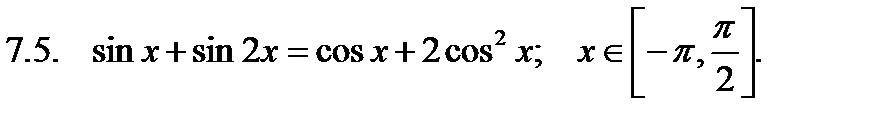
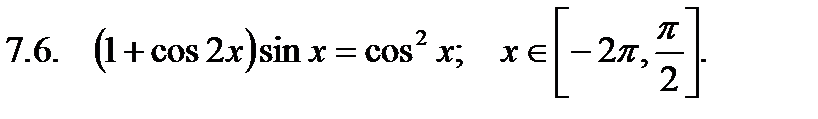
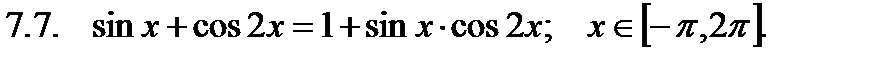
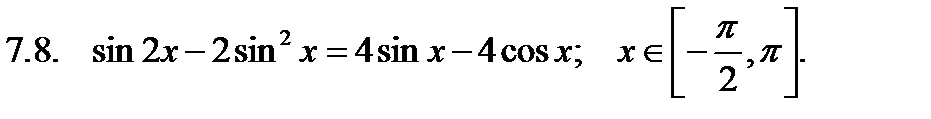
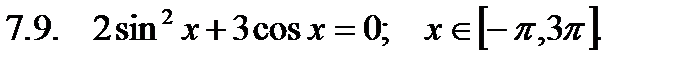
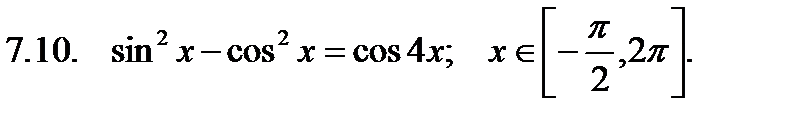
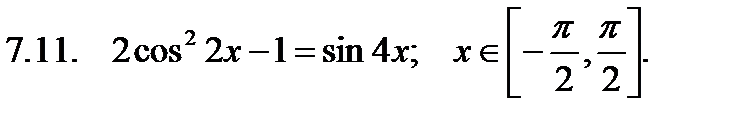
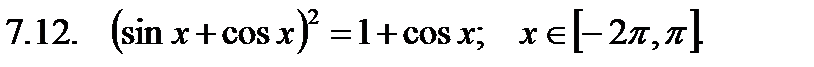
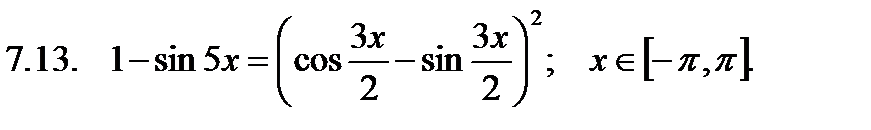
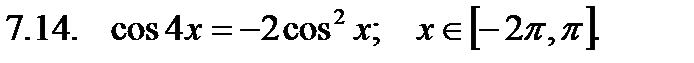
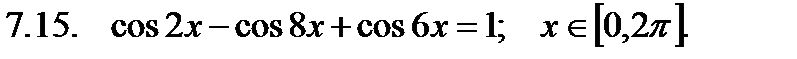
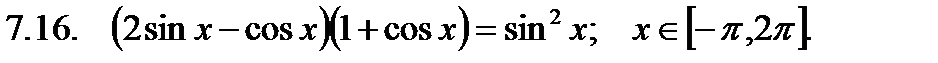
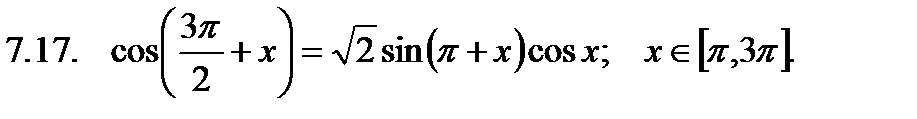
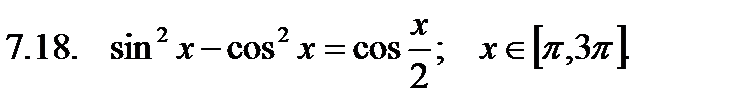
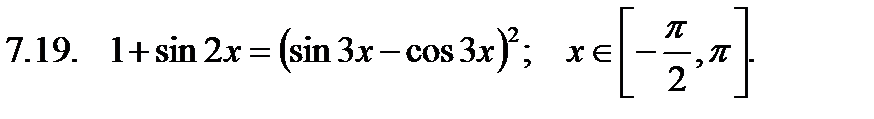
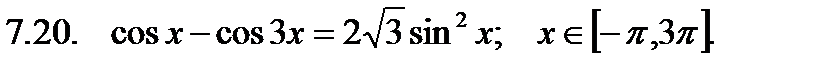
Найти значение производной в точке .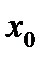

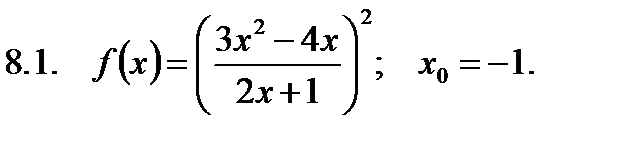
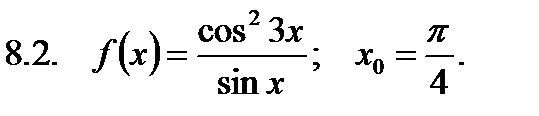
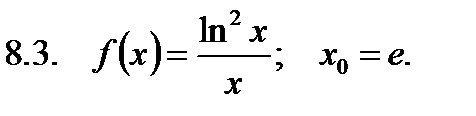
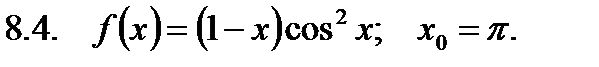
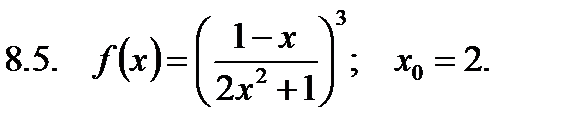
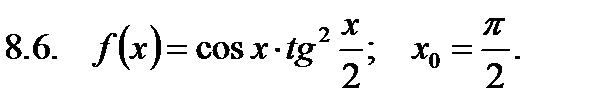
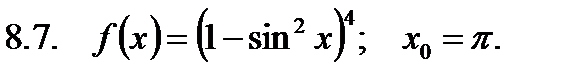
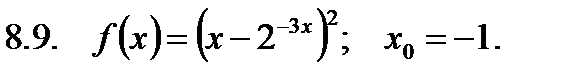
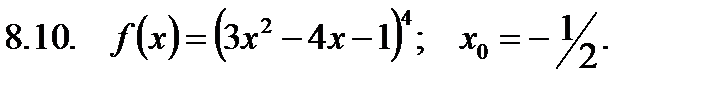
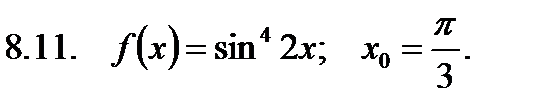
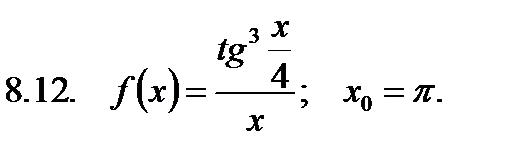
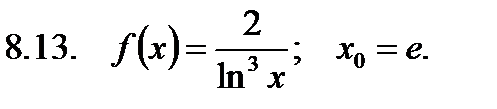
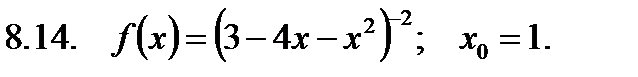
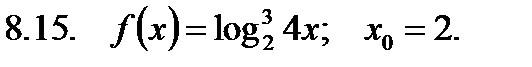
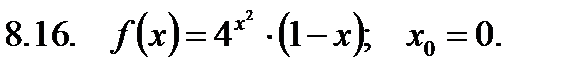
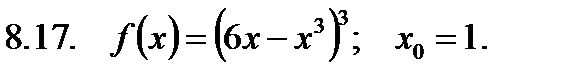
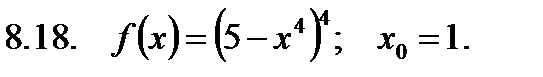
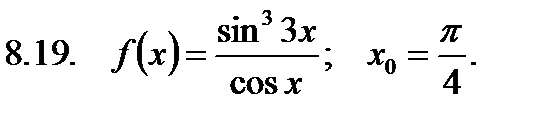
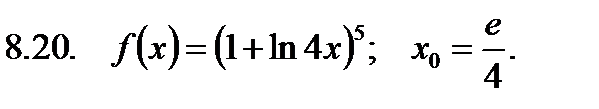
5. Требования к выполнению контрольной работы

К оформлению работы предъявляются следующие требования:

1. Работа выполняется в тетради со свободными полями для замечаний рецензента.

2. На обложке тетради должны быть указаны фамилия и инициалы студента, номер зачётной книжки шифр, номер специальности, срок обучения, название дисциплины.

3. Контрольная работа должна содержать все задачи своего варианта, расположенные в порядке, указанном в задании. Перед решением каждой задачи должны приводиться её условия.

4.Решение следует излагать подробно и аккуратно.

5.В случае получения от рецензента незачтённой работы следует исправить все отмеченные ошибки, внести необходимые исправления и прислать работу для повторной проверки. Рекомендуется при выполнении работы оставлять в конце тетради несколько чистых листов для внесения возможных исправлений после её рецензирования.

Рекомендуемая литература.

1. Алгебра и начала анализа. Учебник для 10 – 11 классов общеобразовательных учреждений под редакцией Ш.А. Алимова, Ю.М Колягина и др. М.: Просвещение, 2011.

2. Алгебра и начала математического анализа. 11 класс,

под редакцией С.М Никольского и др. М.: Просвещение, 2009.

3. Геометрия 10 – 11класс, под редакцией Л.С. Атанасян и др. М.: Просвещение, 2011.

4. ЕГЭ. Математика. Типовые тестовые задания под редакцией А.Л. Семёнова, И.В. Ященко. Изд. „Экзамен” М.: 2011.

5. Э.Ф. Брыжина, Э.С. Коротеева, Н.А. Полозенко.

Математика. Довузовская подготовка. С – П., 2002.

Приложение 1

Содержание дисциплины

(извлечение из рабочей программы)

РАЗДЕЛ 1. АЛГЕБРА

Тема 1.1. Корни и степени. Корень степени n>1 и его свойства. Степень с рациональным показателем. Степень с действительным показателем.

Тема 1.2. Логарифм. Логарифм числа. Свойства логарифмов.

Тема 1.3. Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования.

Тема 1.4. Основы тригонометрии. Определение синуса, косинуса, тангенса, котангенса произвольного угла. Основные тригонометрические тождества. Формулы приведения. Преобразование простейших тригонометрических выражений. Простейшие тригонометрические уравнения. Арксинус, арккосинус, арктангенс числа.

РАЗДЕЛ 2. ФУНКЦИИ

Тема 2.1.Область определения и множество значений. Построение графиков различными способами. Свойства функций. Примеры функциональных зависимостей в реальных процессах и явлениях.

Тема 2.2. Обратная функция. График обратной функции. Степенная функция.

Тема 2.3. Тригонометрические функции, их свойства и графики.

Тема 2.4. Показательная функция. Логарифмическая функция.

Тема 2.5. Преобразование графиков.

РАЗДЕЛ 3. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА

Тема 3.1. Понятие о пределе последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия.

Тема 3.2. Понятие о непрерывности функции.

Тема 3.3. Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной. Таблица производных. Производная обратной и сложной функций.

Тема 3.4. Понятие об определённом интеграле как площади криволинейной трапеции. Первообразная. Формула Ньютона-Лейбница.

Тема 3.5. Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Примеры применения

интеграла в физике и геометрии.

РАЗДЕЛ 4. УРАВНЕНИЯ И НЕРАВЕНСТВА

Тема 4.1.Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных и тригонометрических уравнений.

Тема 4.2. Решение систем уравнений. Равносильность уравнений, неравенств, систем.

Тема 4.3. Применение математических методов для решения содержательных задач из различных областей науки и практики.

РАЗДЕЛ 5. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИ-

КИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ

Тема 5.1. Табличное и графическое представление данных. Числовые характеристики рядов данных.

Тема 5.2. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона.

Тема 5.3. Элементарные и сложные события. Вероятность суммы несовместных событий. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.

РАЗДЕЛ 6. ГЕОМЕТРИЯ

Тема 6.1. Прямые и плоскости в пространстве. Основные понятия стереометрии. Теорема о трёх перпендикулярах. Угол между прямой и плоскостью.

Тема 6.2. Параллельность и перпендикулярность плоскостей. Расстояние от точки до плоскости. Расстояние между скрещивающимися прямыми.

Тема 6.3. Многогранники. Призма, правильная призма. Пирамида, усечённая пирамида, правильная пирамида. Правильные многогранники (тетраэдр, куб, октаэдр, додекаэдр, икосаэдр)

Тема 6.4. Тела и поверхности вращения. Цилиндр и конус, усечённый конус. Шар и сфера, их сечения.

Тема 6.5. Объёмы тел и площади их поверхностей. Отношение объёмов подобных тел.

Тема 6.6. Координаты и векторы. Декартовы координаты в пространстве. Уравнения сферы и плоскости.

Тема 6.7. Векторы. Действия с векторами. Координаты вектора. Скалярное произведение векторов. Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам. Компланарные векторы.

Приложение 2

Перечень контрольных вопросов для проверки знаний по

дисциплине

1. Сформулируйте определение функции.

2. Какую функцию называют сложной?

3. Что такое: а) область существования функции; б) область определения функции; в) область изменения функции?

4. Какую функцию называют: чётной; нечётной?

5. Что называется графиком функции?

6. Какую функцию называют непрерывной на промежутке? 7. Какие функции называют взаимно обратными? Какими свойствами обладают взаимно обратные функции?

8. Что называют приращением аргумента; приращением функции; производной функции?

9. В чём заключается механический смысл производной?

10. В чём заключается геометрический смысл производной?

11. Какую точку отрезка 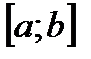называют точкой максимума функции 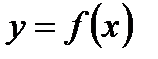; точкой минимума?

12. Объясните порядок отыскания максимума и минимума функции на отрезке.

13. Какими свойствами должна обладать функция 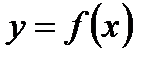, заданная на интервале 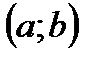, чтобы в точке с абсциссой 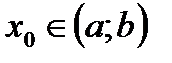её график имел касательную?

14. Какую функцию называют первообразной для функции 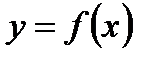на интервале ?

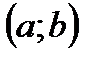15. Что называют неопределённым интегралом от непрерывной на интервале 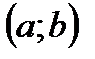функции ?

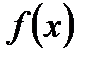16. Как проверить правильность нахождения неопределённого интеграла?

17. Что называют определенным интегралом от функции 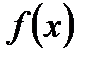на отрезке ?

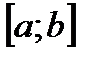18. В чём заключается геометрический смысл определённого интеграла?

19. Какие два уравнения называют равносильными?

20. Какие два неравенства называют равносильными?

21. Какое уравнение называют уравнением-следствием исходного уравнения?

22. Может ли уравнение-следствие иметь корень, не являющийся корнем исходного уравнения?

23. Объясните, почему возведение уравнения в чётную степень может привести к появлению корней, посторонних для исходного уравнения.

24. Какие уравнения называются однородными?

25. Какие уравнения называются иррациональными?

26. Какие системы уравнений называются: совместными; несовместными; определёнными; однородными?

Приложение 3

Дата добавления: 2014-11-06