
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Механический принцип относительности
|
|
|
|
Преобразования Галилея.
Принцип относительности в механике
Уравнения, выражающее второй закон Ньютона  , показывает, что этот закон не может быть справедлив в любой системе отсчета. Ускорение
, показывает, что этот закон не может быть справедлив в любой системе отсчета. Ускорение 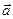 , вообще говоря, имеет разные значения в различных системах отсчета, движущихся относительно друг друга с ускорением. Сила же не может зависеть от выбора системы отсчета (СО), так как она определяется только взаимными расположениями и относительными скоростями материальных точек системы, а эти величины согласно нерелятивистской кинематики от выбора СО не зависят. Отсюда следует, что если II закон Ньютона справедлив в какой-либо СО, то он не может быть справедлив в другой СО, движущейся относительно первой с ускорением.
, вообще говоря, имеет разные значения в различных системах отсчета, движущихся относительно друг друга с ускорением. Сила же не может зависеть от выбора системы отсчета (СО), так как она определяется только взаимными расположениями и относительными скоростями материальных точек системы, а эти величины согласно нерелятивистской кинематики от выбора СО не зависят. Отсюда следует, что если II закон Ньютона справедлив в какой-либо СО, то он не может быть справедлив в другой СО, движущейся относительно первой с ускорением.
Причем сам II закон Ньютона будет справедлив лишь в ИСО, определения которых мы уже давали, когда говорили о законах Ньютона.
Докажем, что уравнения динамики остаются неизменными при переходе от одной ИСО к другой.
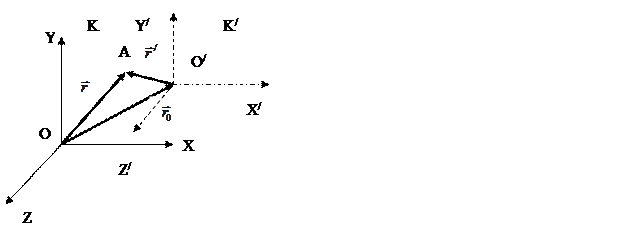
Рассмотрим две СО К и К/, причем К/ движется относительно системы К с постоянной скоростью 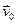 . Пусть система К неподвижна. Отсчет времени начнем с момента, когда начала координат совпадают. Пусть в произвольный момент времени расположение систем относительно друг друга имеет вид:
. Пусть система К неподвижна. Отсчет времени начнем с момента, когда начала координат совпадают. Пусть в произвольный момент времени расположение систем относительно друг друга имеет вид:
|
- эти уравнения называют преобразованиями координат Галилея.
Если система К/ движется со скоростью 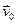 вдоль положительного направления оси Х, получим:
вдоль положительного направления оси Х, получим:  ,
, 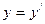 ,
, 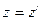 .
.
В классической механике считают, что ход времени не зависит от относительного движения систем отсчета, т.е. к преобразованиям 1 или 2 добавляют  (3).
(3).
Отметим, что записанные соотношения справедливы лишь в случае классической механики ( ). При
). При  сравнимой со скоростью света преобразования Галилея должны быть заменены более общими преобразованиями, которые мы еще рассмотрим.
сравнимой со скоростью света преобразования Галилея должны быть заменены более общими преобразованиями, которые мы еще рассмотрим.
Продифференцируем (1) по времени с учетом (3):  ;
; 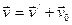 (4) - это правило сложения скоростей в классической механике. В проекциях оно имеет вид:
(4) - это правило сложения скоростей в классической механике. В проекциях оно имеет вид:  ,
,  ,
, 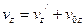 .
.
Ускорение т. А в системе отсчета К: 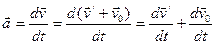 , так как
, так как 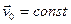 , то
, то 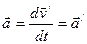 . Мы получили, что ускорение точки в системах отсчета К и К/, движущихся относительно друг друга равномерно и прямолинейно, одинаково:
. Мы получили, что ускорение точки в системах отсчета К и К/, движущихся относительно друг друга равномерно и прямолинейно, одинаково: 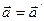 (5).
(5).
Умножив правую и левую части соотношения (5) на массу, которая не зависит от состояния движения (во всех ИСО она остается постоянной):  или
или 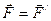 .
.
Мы доказали механический принцип относительности (принцип относительности Галилея): законы механики одинаковы во всех инерциальных системах отсчета, то есть являются инвариантными по отношению к преобразованиям координат.
Галилей отметил, что никакими механическими опытами, проведенными «внутри» данной инерциальной системы отсчета, невозможно установить покоится данная система или движется прямолинейно и равномерно. Пример: сидя в каюте корабля, движущегося прямолинейно и равномерно, нельзя определить, покоится он или движется, не выглянув в окно.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 401; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 - радиус-вектор, соединяющий начало координат О и О/
- радиус-вектор, соединяющий начало координат О и О/ 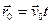 . Найдем связь координат т. А в обеих системах отсчета.
. Найдем связь координат т. А в обеих системах отсчета. 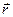 и
и  - радиус-вектора точки в системах
К и К/. Из рисунка видно, что
- радиус-вектора точки в системах
К и К/. Из рисунка видно, что  или
или 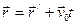 (1). Если записать в
проекциях на оси координат:
(1). Если записать в
проекциях на оси координат:
 ,
, 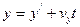 ,
, 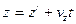 (2)
(2)