Каноническое уравнение прямой. Параметрические уравнения прямой

Параметрические уравнения прямой.

Замечая, что , , , уравнение (9) можно записать в виде

.

Отсюда следуют равенства:

,

, (10)

.

Они называются параметрическими уравнениями прямой в пространстве.

Пусть 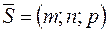— направляющий вектор прямо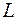й и 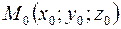— точка, лежащая на этой прямой. Вектор 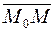, соединяющий точку с произвольной точкой 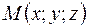прямой 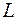, параллелен вектору 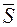. Поэтому координаты вектора 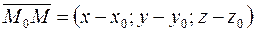и вектора 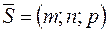пропорциональны:

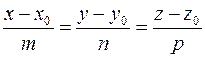. (11)

Уравнение (11) называются каноническим уравнением прямой в пространстве.

Замечания: 1) Уравнения (11) можно было бы получить сразу из параметрических уравнений прямой (10), исключив параметр 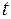. Из уравнений (10) находим

.

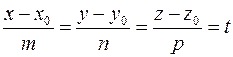2) Обращение в нуль одного из знаменателей уравнений (11) озна­чает обращение в нуль соответствующей координаты направляющего вектора прямой.

Например, уравнения задают прямую, проходящую через точку 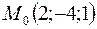перпендикулярно оси 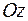(проекция вектора 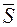на ось 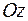равна нулю). Но это означает, что прямая лежит в плоскости , и поэтому для всех точек прямой будет .

Дата добавления: 2014-11-06