Тема №6 2 страница

Произведение любого вектора на нуль и нуль-вектора на любое число, по определению, есть нуль-вектор, т.е. = , = .

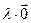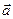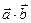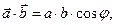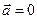Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла j между ними. Обозначение: или , т.е. где Если или 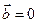, то, по определению,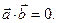

Декартова прямоугольная система координат в пространстве называется правой (левой), если поворот от базисного вектора 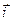к вектору на наименьший угол виден с конца вектора осуществляющимся против (по) часовой стрелки. Говорят также, что тройка базисных векторов имеет правую (левую) ориентацию.

Векторным произведением двух неколлинеарных векторов 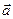и называется вектор 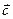, перпендикулярный плоскости векторов 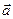и , имеющий длину, равную площади параллелограмма, построенного на векторах 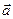и и направленный так, что тройка векторов 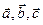так же ориентирована, как и тройка базисных векторов . Обозначение: . Векторное произведение двух коллинеарных векторов и в случае, когда один или оба сомножителя - нуль-векторы, по определению, равно нулю.

Смешанным произведением трех векторов 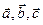называется скалярное произведение векторного произведения первых двух векторов на третий. Обозначение: , т.е. 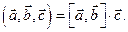Из этого определения следует, что три вектора компланарны (параллельны одной плоскости) тогда и только тогда, когда их смешанное произведение равно нулю.

Любая прямая на плоскости может быть задана уравнением первого порядка 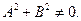Это уравнение называют общим уравнением прямой.

Каждый ненулевой вектор 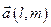, компоненты которого удовлетворяют условию называется направляющим вектором прямой .

Направляющими косинусами прямой называются направляющие косинусы вектора 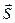, которые могут быть вычислены по формулам:

; .

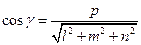Откуда 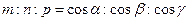. Числа называются угловыми коэффициентами прямой.

Пусть - произвольное множество действительных чисел: . Говорят, что задана функция с областью определения D, если каждому числу 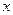из множества D поставлено в соответствие единственное действительное число 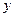. Обозначение: . Читается: «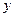 есть от 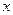. Число 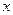называется аргументом, число 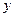- значением функции при данном значении 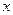аргумента. Множество 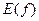всех значений функции называется областью значений этой функции.

Графиком функции называется множество точек координатной плоскости, где 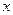«пробегает» всю область определения .

Число 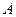называется пределом функции 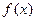при , если для любого 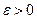существует такое число , что для всех 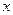таких, что 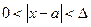верно неравенство .

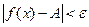Если при только при , то - называется пределом функции 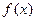в точке слева, а если при только при , то 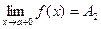называется пределом функции 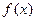в точке справа.

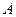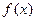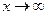Число называется пределом функции при , если для любого числа 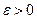существует такое число 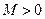, что для всех 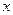, таких что выполняется неравенство . При этом предполагается, что функция 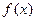определена в окрестности бесконечности. Обозначение: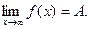

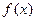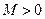Функция называется ограниченной в некоторой окрестности точки , если существует такое число , что 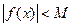для всех точек 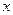из этой окрестности.

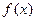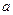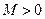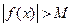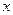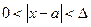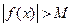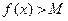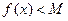Предел функции при , где - число, равен бесконечности, если для любого числа существует такое число , что неравенство выполняется для всех , удовлетворяющих условию . Обозначение: . Если в приведенном определении заменить условие на , то получим а если заменить на , то

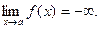
Функция называется бесконечно большой при , где 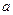– число или одна из величин ¥, +¥, -¥, если , где А –число или одна из величин ¥, +¥, -¥.

Если , то функция называется бесконечно малой более высокого порядка, чем функция .

Если , то и называются бесконечно малыми одного порядка малости.

Если 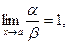то функции и называются эквивалентными бесконечно малыми. Обозначение: .

Бесконечно малая функция называется бесконечно малой порядка k относительно бесконечно малой функции , если предел 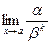существует, конечен и отличен от нуля.

Функция 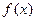, определенная в некоторой окрестности точки , называется непрерывной в точке , если предел функции и ее значение в этой точке равны 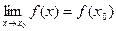. Тот же факт можно записать иначе: .

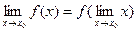Если функция 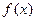определена в некоторой окрестности точки , но не является непрерывной в самой точке , то она называется разрывной функцией в этой, а сама точка называется точкой разрыва этой функции.

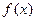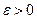Функция называется непрерывной в точке , если для любого положительного числа существует такое число , что для любых 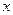, удовлетворяющих условию , выполняется неравенство .

Функция 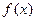называется непрерывной в точке , если приращение функции в точке является величиной бесконечно малой в этой точке где – функция бесконечно малая при 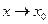. Если функция непрерывна в каждой точке множества , то говорят, что она непрерывна на множестве .

Точка называется точкой устранимого разрывафункции , если в этой точке функция имеет конечные, равные друг другу левый и правый пределы, не равные значению функции в точке : 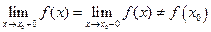. При этом в самой точке функция может быть и не определена. Если доопрпеделить значение функции в точке положив его равным , то функция будет непрерывной в точке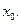

Точка называется точкой разрыва 1- го рода функции , если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы

.

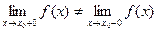Точка называется точкой разрыва 2 – го рода функции , если один из односторонних пределов функции 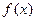в этой точке либо не существует либо равен бесконечности.

Функция 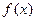называется непрерывной на интервале (отрезке), если она непрерывна в каждой точке интервала (отрезка).

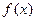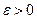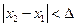Функция называется равномерно непрерывной на отрезке , если для любого существует такое, что для любых точек и таких, что выполняется неравенство .

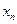Если каждому натуральному числу поставлено в соответствие по некоторому закону определённое число , то говорят, что на множестве всех натуральных чисел задана последовательность Общий член последовательности является функцией от . Таким образом, последовательность является функцией натурального аргумента.

Последовательность 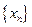называется ограниченной, если существует такое число 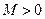, что для любого справедливо неравенство 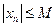, т.е. все члены последовательности принадлежат отрезку .

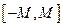Последовательность 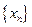называется ограниченной сверху, если для любого существует такое число , что .

Последовательность 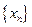называется ограниченной снизу, если для любого n существует такое число , что .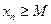

Число 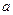называется пределом последовательности 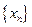, если для любого положительного 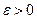существует такой номер , что для всех 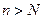выполняется неравенство 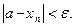Обозначение: . В этом случае говорят, что последовательность 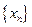сходится к 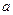при .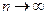

1) Если для всех , то последовательность называется возрастающей.

2) Если для всех , то последовательность называется неубывающей.

3) Если для всех , то последовательность называется убывающей.

4) Если 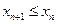для всех , то последовательность называется невозрастающей.

Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.

Производной функции в точке называется предел, если он существует, отношения приращения функции в точке к приращению аргумента 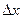в этой точке, когда последнее стремится к нулю 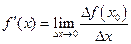, где - приращение аргумента в точке , а 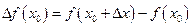- соответствующее этому приращению приращение функции в этой точке.

Правой (левой) производной функции в точке называется правый (левый) предел , при условии, что этот предел существует. Если функция имеет производную в некоторой точке , то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно.

Дифференциалом функции в точке 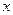называется главная линейная часть приращения функции. Обозначается или . Из определения следует, что или 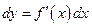, так как 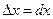. Следовательно, .

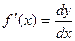Формулой Маклорена называется формула Тейлора при :

Пусть функция дифференцируема на некотором интервале. Дифференцируя, находим её первую производную . Если найти производную функции 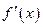, получим вторую производную функции если последняя существует , т.е. или .Этот процесс можно продолжить и далее, находя производные степени .

Функция имеет в точке 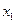максимум, если ее значение в этой точке больше значений во всех точках некоторой окрестности, содержащей точку 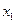. Функция имеет в точке минимум, если при любом 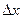( 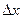может быть и отрицательным).

Дата добавления: 2014-11-06