Тема №6 3 страница

Точки максимума и минимума функции называются точками экстремума.

Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.

Кривая называется выпуклой (вогнутой) на интервале 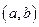, если все ее точки лежат не выше (не ниже) любой ее касательной на этом интервале.

Точка, при переходе через которую направление вогнутости кривой меняется на противоположное, называется точкой перегиба.

Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой стремится к нулю при удалении этой точки на бесконечность.

Дифференцируемая на некотором промежутке 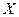функция 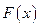называется первообразной для функции , определенной на том же промежутке, если для каждого числа 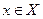выполняется равенство .

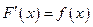Пусть на отрезке задана непрерывная функция . Обозначим через m и M наименьшее и наибольшее значение функции на отрезке . Разобьем отрезок на части (не обязательно одинаковые) n точками 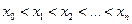. Введём обозначения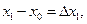 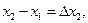… 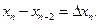На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции:

, , … .

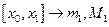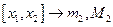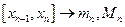Составим суммы:

=

= .

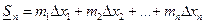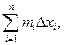
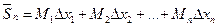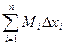Сумма 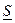называется нижней интегральной суммой, а сумма – верхней интегральной суммой, соответствующей данному разбиению отрезка.

Если существует конечный предел 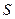последовательности интегральных сумм 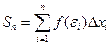при 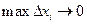, не зависящий ни от разбиения отрезка на части ни от выбора в этих частях промежуточных точек, то этот предел называется определённым интегралом от функции по отрезку , а функция называется интегрируемой по Риману на отрезке . По определению

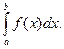Обозначение: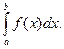

Число 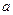называется нижним пределом интегрирования, а число 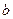верхним пределом интегрирования; 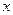называется переменной интегрирования; – отрезок интегрирования.

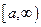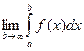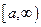Пусть функция определена и непрерывна на интервале . Тогда она непрерывна и, следовательно, интегрируема на любом конечном отрезке . Предел называется несобственным интегралом от функции на интервале . Обозначение: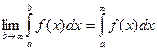

Если этот предел существует и конечен, то говорят, что несобственный интеграл называется сходящимся. Если предел не существует или бесконечен, то несобственный интеграл называется расходящимся. Аналогичные рассуждения можно привести для несобственных интегралов вида:

,

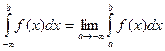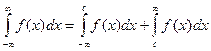
при условии, если входящие в них интегралы существуют.

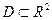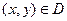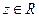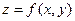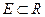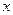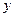Пусть дано множество , и пусть указано правило (закон), по которому каждой точке ставится в соответствие единственное действительное число . В этом случае говорят, что задана функция с областью определения и областью значений . При этом и называют независимыми переменными (аргументами), а 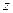– зависимой переменной (функцией). Функцию 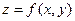иногда записывают в виде .

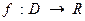Открытый круг радиуса 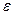с центром в точке 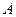называется 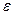-окрестностью точки .

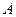Точка 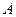называется внутренней точкой множества 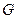, если существует 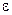-окрестность 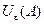точки 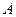, целиком принадлежащая множеству 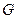(т.е. ).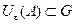

Точка 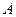называется граничной точкой множества 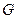, если в любой ее 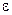-окрестности содержатся точки, как принадлежащие множеству 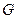, так и не принадлежащие ему.

Множество 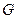называется открытым, если все его точки – внутренние.

Множество 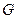называется замкнутым, если оно содержит все свои граничные точки. Множество всех граничных точек множества 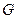называется его границей (и часто обозначается символом 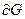). Заметим, что множество 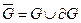является замкнутым и называется замыканием множества .

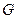Точка 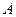называется предельной точкой множества 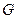, если в любой 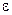-окрестности точки 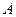содержатся точки множества 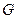, отличные от .

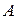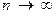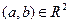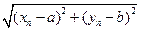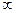Говорят, что последовательность точек сходится при к точке , если стремится к 0 при стремящемся к . В этом случае точку 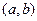называют пределом указанной последовательности и пишут: 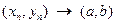при .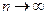

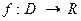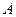Пусть и – предельная точка множества . Число называют пределом функци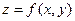и при 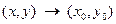, если для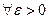 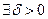такое, что 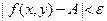, как только 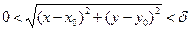. В этом случае пишут

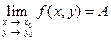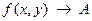или при .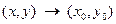

Число 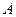называют пределом функции 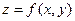при и 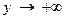, если для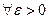 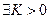такое, что из неравенств 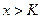и 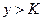следует неравенство 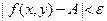. Этот факт коротко записывают так .

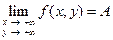Пусть дана функция 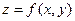с областью определения и пусть – предельная точка множества 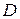. Говорят, что функция 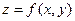непрерывна в точке , если

1) ;

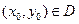2) 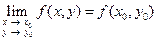, т.е. .

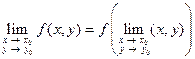Обозначим , 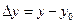и 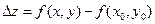. Говорят, что функция 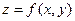непрерывна в точке , если выполняется равенство .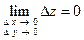

Функция 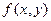, определённая на некотором множестве 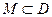называется непрерывной на множестве если она непрерывной в каждой точке множества .

Множество 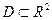называется областью, если оно:

1) является открытым множеством, т.е. содержит каждую свою точку вместе с некоторой своей 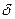-окрестностью; 2) является линейно связным множеством, т.е. для любых двух различных точек 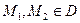существует ломаная, соединяющая 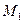и 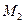и целиком лежащая в . Если – область, то множество 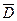называют замкнутой областью.

Говорят, что функция непрерывна в области (или в замкнутой области 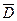), если непрерывна в каждой точке этой области.

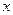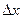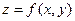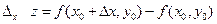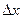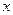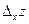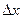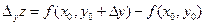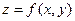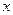Зафиксируем переменную , а переменной придадим произвольное приращение . Функция получит приращение , которое называется частным приращением функции в точке , соответствующим приращению аргумента . Заметим, что является функцией одной переменной . Аналогично, . Функция называется непрерывной в точке по переменной ( по переменной 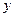), если 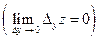. В отличие от непрерывности по отдельным переменным обычную непрерывность функции называют иногда непрерывностью по совокупности переменных.

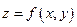Пусть в некоторой области задана функция . Возьмем произвольную точку 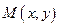из этой области и дадим переменной х приращение 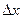. Величина 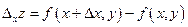называется частным приращением функции по х. Рассмотрим отношение 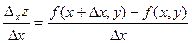. Если существует конечный предел 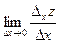, то он называется частной производной функции 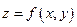по х. Обозначение: 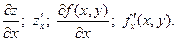Аналогично определяется частная производная функции 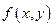по у: .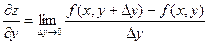

Выражение 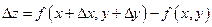называется полным приращением функции 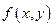в точке .

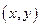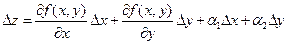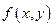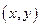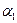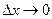Выражение называется полным приращением функции в точке , где и – бесконечно малые функции при и 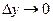соответственно.

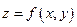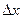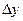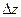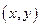
Полным дифференциалом функции называется главная, линейная относительно и часть приращения функции в точке 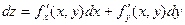. Для функции произвольного числа переменных имеем:

.

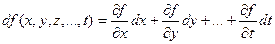Нормалью к поверхности в точке 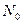называется прямая, проходящая через точку 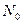перпендикулярно касательной плоскости к этой поверхности. Если поверхность задана уравнением 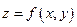, где 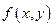– функция, дифференцируемая в точке 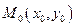, то касательная плоскость в точке 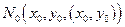существует и определяется уравнением: .

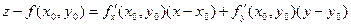Частные производные по различным аргументам вида 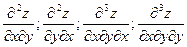и т.д. называются смешанными производными.

Дифференциалом второго порядка (вторым дифференциалом) функции 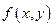называется дифференциал от её первого дифференциала:

.

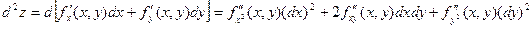Аналогично определяются дифференциал третьего порядка от функции :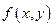

Пусть функция 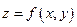определена в некоторой области , и 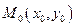- произвольная точка этой области. Если для всех точек 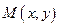из некоторой окрестности точки 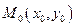выполняется неравенство: 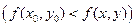то точка 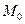называется точкой локального максимума (локального минимума) функции 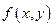в области .

Точки локального максимума и локального минимума функции 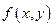называются точками экстремума этой функции. Рассмотрим функцию 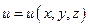в точках и 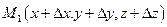. Построим вектор 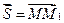. Углы наклона этого вектора к положительным направлениям координатных осей 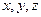обозначим соответственно 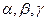. Косинусы этих углов называются направляющими косинусами вектора .

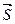Предел 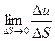называется производной функции 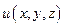по направлению вектора 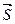в точке с координатами .

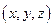Если в некоторой области D задана функция 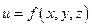и некоторый вектор, проекции которого на координатные оси равны значениям функции в соответствующей точке 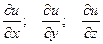, то этот вектор называется градиентом функции . Обозначение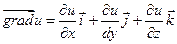

Дифференциальным уравнением называется уравнение, связывающее независимые переменные, неизвестные функции и производные различных порядков от неизвестных функций по независимым переменным.

Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.

Общим решением дифференциального уравнения называется дифференцируемая функция одного или нескольких аргументов, которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

Решение вида 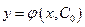называется частным решением дифференциального уравнения.

Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида 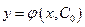, удовлетворяющего начальным

Интегралом дифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.

Интегральной кривой называется график 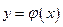решения дифференциального уравнения на плоскости .

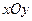Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности решения задачи Коши не выполняется, т.е. в окрестности некоторой точки 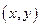существует не менее двух интегральных кривых.

Дата добавления: 2014-11-06