Порядок визначення варіанта контрольної роботи

ЕКОНОМЕТРІЯ

ТЕОРЕТИЧНА ЧАСТИНА КОНТРОЛЬНОЇ РОБОТИ

Варіант визначається за двома останніми числами залікової книжки. Якщо дві останні цифри від 01 до 30, то ці дві цифри складають номер варіанта. Якщо дві останні цифри складають число від 31 до 60, то необхідно відняти 30, від 61 до 90 необхідно відняти 60, 91 до 99 необхідно відняти 90.

Якщо дві останні цифри 00 студент виконує варіант №10.

Теоретична частина контрольної роботи вибирається за варіантом із питань до заліку (для кожного варіанта визначені номери питань)

Варіант	Номер питання із питань до заліку
1.	1, 11, 41
2.	2, 12, 42
3.	3, 13, 43
4.	4, 14, 44
5.	5, 15, 45
6.	6, 16, 46
7.	7, 17,47
8.	8, 18, 48
9.	9, 19, 49
10.	10, 20, 30
11.	11, 21, 50
12.	12, 22, 51
13.	13, 23, 52
14.	14, 24, 53
15.	15, 25, 54
16.	16, 26, 31
17.	17, 27, 32
18.	8, 16, 36
19.	19, 29, 34
20.	20, 31,51
21.	21, 32, 52
22.	22, 11, 18
23.	23, 12, 32
24.	24, 17, 53
25.	25, 18, 54
26.	26, 11, 9
27.	27, 10, 8
28.	28, 10, 17
29.	29, 50, 32
30.	30, 8, 2

Задача 3.

Для побудови економетричної моделі, що характеризує залежність попиту на певну продукцію від доходу на одну особу, ціною одиниці товару та ціною одиниці взаємозамінюваних товарів, необхідно перевірити гіпотезу про наявність (чи відсутність) гетероскатендичності для вихідних даних, наведених в таблиці 1.

Таблиця 1.

Місяць	Попит, грн.	Дохід на одну особу, грн.	Ціна один. товару, грн.	Ціна взаємозамінних товарів, грн.
1-й	50,00	200,00	22,00	2,00
2-й	52,00	210,00	51,00	3,00
3-й	51,00	205,00	51,50	2,50
4-й	55,00	220,00	19,00	4,00
5-й	56,00	225,00	18,00	5,00
6-й	54,00	220,00	18,50	4,50
7-й	60,00	230,00	16,00	6,00
8-й	58,00	228,00	17,00	9,00
9-й	62,00	240,00	15,00	10,00
10-й	64,00	250,00	12,00	11,00
11-й	65,00	255,00	11,00	11,00
12-й	67,00	260,00	11,00	12,00

Основні теоретичні положення

Однією з умов для ефективності оцінювання параметрів моделі 1МНК є незміність дисперсії залишків для всіх спостережень вихідної сукупності. Це явище називають гомоскедантичністю. На практиці воно часто порушується.

Наприклад, в економетричній моделі, що характеризує залежність витрат на споживання від доходу, дисперсія залишків може змінюватись для спостережень, які характеризують розмір доходів різних груп населення.

Якщо дисперсія залишків при побудові економетричної моделі змінюється для кожного спостереження або груп спостережень, то це явище називається гетероскедантичністю.

При геретоскедантичністю дисперсія залишків така:

,

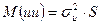Де: S – діагональна додатково визначена матриця розміром .

Гетероскедантичність призводить до порушення властивостей незміщеності та ефективності оцінок параметрів моделі, здобутих за допомогою 1МНК, тому, якщо існує гетероскедастичність, то для оцінювання параметрів моделі застосовують узагальнений метод найменших квадратів (метод Ейткена).

Для визначення гетероскедантичності застосовують такі критерії:

1) критерій ;

2) параметричний тест Гольдфельда-Квандта;

3) непараметричний тест Гольдфельда-Квандта;

4) тест Глей сера.

Коли вихідна сукупність спостережень досить велика, то застосовують метод, основний на критерію .

Алгоритм критерію .

1. Вихідні дані залежної змінної Y розбивають на к груп відповідно до зміни рівня величини Y.
2. Для кожної групи даних обчислюється сума квадратів відхилень:

.

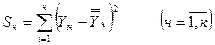1. Визначається сума квадратів відхилень у цілому по всій сукупності спостережень:

.

1. Обчислюємо параметр :

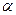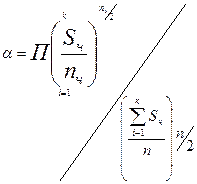
Де: п – загальна кількість спостережень;

- кількість спостережень ч-ї групи.

1. Обчислюємо критерії :

,

Який наближено відповідатиме 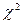при ступені свободи к-1, за умови, що дисперсія всіх спостережень однорідна. Якщо при вибраному рівні довіри та ступені свободи к-1, то спостерігається гетероскедантичність.

Для розв’язання задачі використаємо параметричний тест Гольдфельда-Квандта.

1. Ідентифікуємо змінні:

Y – попит (залежна змінна);

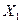- дохід на одну людину (незалежна або пояснювальна змінна);

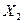- ціна одиниці товару (незалежна або пояснювальна змінна);

- ціна одиниці взаємо замінюваних товарів (незалежна або пояснювальна змінна).

Загальний вигляд моделі: ,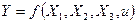

Де: u – стохастична складова.

1. Специфікуємо економетричну модель у лінійній формі:

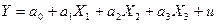
І очікувана модель:

.

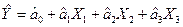
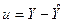1. Досліджувану сукупність спостережень впорядковуємо за 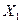від меншого значення до більшого:

Таблиця 2.

№ з/п	Y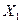
	50,00	200,00
	51,00	205,00
	52,00	210,00
	55,00	220,00
	54,00	220,00
	56,00	225,00
	58,00	228,00
	60,00	230,00
	62,00	240,00
	64,00	250,00
	65,00	255,00
	67,00	260,00

Відшукуємо з спостережень, які містяться всередині сукупності:

n=12, по с=3.

Отже, якщо ми відкинемо 3 елементи із середини, то в сукупності залишиться 9 елементів, які не діляться на 2 без остачі. Тому потрібно відкинути 3 елементи із середини та 1 елемент на початку сукупності й дістанемо дві сукупності 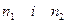по чотири елементи.

1. Будуємо дві економетричні моделі за двома створеними сукупностями:

Таблиця 3.

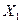
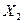
51,00	205,00	62,00	240,00
52,00	210,00	64,00	250,00
55,00	220,00	65,00	255,00
54,00	220,00	67,00	260,00

Для сукупності :

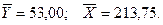
Таблиця 4.

№ з/ п	Y	X		XY
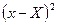
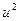
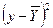
					51,5 3	-8,75	-2	76,5625	17,5	-0,53	0,2809
					52,73	-3,75	-1	14,0625	3,75	-0,73	0,5329
					55,13	6,25		39,0625	12,5	-0,13	0,0169
					55,13	6,25		39,0625	6,25	-1,13	1,2769
					-	-	-	168,75		-	2,1076	-

Система рівнянь для визначення :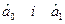

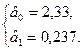
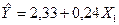
Для сукупності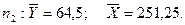

Таблиця 5.

№ з/ п	Y	X		XY
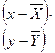
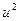
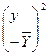
					61,8	-11,25	-2,5	126,5625	28,125	0,2	0,04	6,25
					64,2	-1,25	-0,5	1,5625	0,625	-0,2	0,04	0,25
					65,4	3,75	0,5	14,0625	1,875	-0,4	0,16	0,25
					66,6	8,75	2,5	76,5625	21,875	0,4	0,16	6,25
					-	-	-	218,75	52,5	-	0,40	-

Система рівнянь для визначення :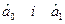

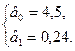
Сума квадратів залишків:

Критерій .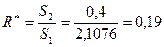

Порівняємо ці значення з табличним значенням критерію Фішера (F-критерію) при 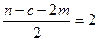ступені свободи та 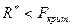У масиві 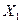гетероскедантичність відсутня.

1. Перевіримо на гетероскедантичність 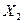. Впорядкуємо 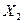від меншого до більшого значення:

Таблиця 6.

№ з/п
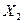
		18,50
		21,50

Відкинемо один елемент спочатку та 3 елементи із середини та одержимо дві сукупності по 4 елементи. Позначимо їх .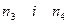

Таблиця 7.

			21,5

Для сукупності .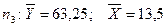

Таблиця 8.

№ з/ п	Y	X		XY
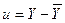
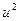
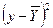
					59,26	-2,5	3,75	6,25	-9,375	7,74	59,91	14,0625
					58,02	-1,5	0,75	2,25	-1,125	5,95	35,4	0,5625
					54,43	1,5	-1,25	2,25	-1,875	7,57	57,30	1,5625
					53,23	2,5	-3,25	6,25	-8,175	6,77	45,83	10,5625
					-	-	-		-20,55	-	198,44	-

Система рівнянь для визначення :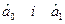

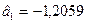
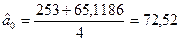
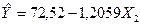
Для сукупності

Таблиця 9.

№ з/ п	Y	X		XY
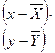
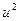
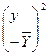
					55,07	-1,88		3,5344	-5,64	-0,07	0,0049
					51,79	0,12		0,0144		0,21	0,0441
		21,5	462,25	1096,5	50,97	0,62	-1	0,3844	-0,62	0,03	0,0009
					50,15	1,12	-2	1,2544	-2,24	-0,15	0,0225
		83,5	1748,25	4333,5	-	-	-	4,1876	-8,5	-	0,0724	-

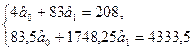
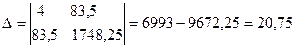
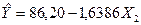
Суми квадратів залишків:

Критерій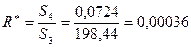

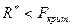Отже в масиві 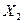гетероскедантичність відсутня.

1. Перевіримо на гетероскедантичність . Впорядкуємо від меншого до більшого значення:

Таблиця 10.

№ з/п
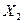
		2,5
		4,5

Відкинемо один елемент спочатку та 3 елементи із середини та одержимо дві сукупності по 4 елементи. Позначимо їх .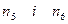

Для сукупності

Таблиця 11.

№ з/ п	Y	X		XY
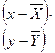
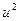
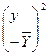
		2,5	6,25	127,5		-1	-2,5		2,5			6,25
					64,5		-0,5			-0,5	0,25	0,25
					64,5		0,5			0,5	0,25	0,25
		4,5	20,25				2,5		2,5			6,25
			51,5	746,5	-	-	-		5,0	-	0,5	-

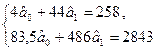
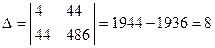
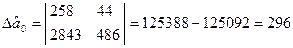
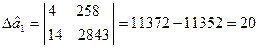
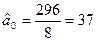
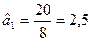
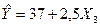
Суми квадратів залишків:

Критерій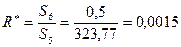

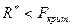. Отже в масиві гетероскедантичність відсутня.

Чистій гетероскедантичності відповідають значення параметрів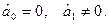

Змішаній - . Метод параметричного тесту Гольдфельда-Квандта не дае відповіді на питання чи існує змішана гетероскедантичність.

Питання до заліку

1. У чому полягає основний зміст проблематики економетрії?
2. Надати тлумачення поняття «математична модель економічного об’єкта».
3. Який зміст основних етапів проведення економічного аналізу?
4. Римський клуб. Надати ілюстрацію результатів його роботи.
5. Модель Леонтьева та її економічне тлумачення.
6. Навести приклади основних задач, що розглядаються в економетрії.
7. У чому полягає відмінність між поняттями «динамічний ряд» та «варіантний ряд»?
8. Дати визначення та економічну інтерпретацію основних статистичних характеристик динамічного ряду: середньої хронологічної, дисперсії, середнього квадратичного відхилення, середнього абсолютного приросту, середніх коефіцієнтів зростання та приросту, ступеню коливання.
9. Що називається частотою варіанти? Як обчислити середнє арифметичне варіаційного ряду та дисперсію по наявних частотах варіант?
10. Що називається метрикою простору, які її властивості?
11. Дати визначення евклідової та манхетичної метрики.
12. Дати визначення виробничої функції та вказати область її застосування.
13. Дати тлумачення поняття «умови праці та стан зовнішнього середовища».
14. Описати загальний метод побудови емітричної виробничої функції.
15. Описати методи найменших квадратів і робастного оцінювання параметрів виробничої функції.
16. У чому полягає внесок Кобба Та Дугласа в теорію виробничих функцій?
17. Описати правило визначення параметрів лінійної регресії двох змінних в методі найменших квадратів. Дати тлумачення цього правила.
18. Назвіть основні властивості лінійної регресії, вибір параметрів якої проводиться за методом найменших квадратів.
19. Як визначається коефіцієнт кореляції? Які його основні властивості?
20. Надати тлумачення поняття «ступінь вільності».
21. Які статистичні характеристики спостережувального показника містить ANOVA-таблиця?
22. У яких випадках прийнято перевіряти просту регресійну модель на адекватність за допомогою F-критерія Фішера? У чому саме полягає ця перевірка?
23. Які критерії якості лінійної регресії, відмінні від F-критерія Фішера, використовують на практиці?
24. Надати імовірнісне тлумачення вибору параметрів регресії за даними спостережень?
25. За яких умов можна підрахувати математичне сподівання та дисперсії параметрів лінійної регресії?
26. Як прийнято оцінювати дисперсію випадкової величини в моделі лінійної регресії?
27. Як визначити довірчий інтервал для нормального розподіленої випадкової величини з відомими параметрами розподілу?
28. Як побудувати довірчий інтервал для нормально розподіленої випадкової величини, для якої відоме математичне сподівання та оцінка дисперсії, що має 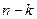ступені вільності?
29. Як побудувати довірчі інтервали параметрів лінійної регресії?
30. У чому полягає відмінність між точковим та інтервальними прогнозами?
31. Як будується інтервальний прогроз значень залежної змінної в моделі лінійної регресії?
32. Наведіть приклади нелінійних функціональних залежностей, що використовуються в економічному аналізі.
33. Навести економічне тлумачення зв’язку між параметрами, що виражається логістичною функцією (x – загальна кількість певного товару на ринку, y – величена прибутку отриманого від реалізації).
34. Побудувати графік експонеційної залежності. Як можна обчислити за методом найменших квадратів параметри експлнеційної залежності при ?
35. Побудувати графік кривої Гомперця.
36. Навести економічне тлумачення коефіцієнта еластичності.
37. Навести приклади застосування багатофакторного регресійного аналізу.
38. Дати визначення лінійної багатофакторної регресійної моделі. При яких основних припущеннях досліджується ця модель?
39. Прокоментувати основні етапи побудови лінійної багатофакторної регресивної моделі.
40. Як розраховуються невідомі параметри лінійної моделі багатофакторної регресії за методом МНК?
41. Які основні властивості методу найменших квадратів у випадку багатофакторної лінійної регресії.
42. Як визначаються коефіцієнти множинної кореляції та детермінації у багатофакторній регресійній моделі?
43. Як визначається оцінений коефіцієнт детермінації? Зазначити його основні властивості.
44. Описати зміст ANOVA-таблиці у випадку багатофакторної регресії.
45. У чому полягає правило перевірки на адекватність багатофакторної регресійної моделі за F-критерієм Фішера?
46. Як побудувати інтервали довіри для параметрів багатофакторної регресії?

47. В чому полягають теоретичні і практичні наслідки мультиколінеарності?

1. Які методи та критерії використовують для виявлення мультиколінеарності?
2. Дати визначення допоміжної регресії та описати умови та спосіб її використання.
3. До чого може привести вилучення з регресійної моделі залежного фактора?
4. Які особливості (економічного) явища можна дослідити використовуючи dummy-змінні?
5. Навести приклади регресійних моделей, у яких застосовують dummy-змінні.
6. Які регресійні моделі називають дистрибутивно-лаговими? Авто регресивними?
7. Навести приклад лінійної дистрибутивно-лагової регресійної моделі.

Дата добавления: 2014-11-06