Примеры с решениями. Пример 2.1. Тензор напряжений в точке Р, отнесенный к осям , имеет вид

Пример 2.1. Тензор напряжений в точке Р, отнесенный к осям 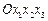, имеет вид 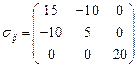. Пусть новые оси 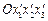получены поворотом около начала отсчета, т.е. преобразованием с матрицей 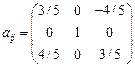. Определить вектор напряжений на каждой из координатных площадок системы со штрихами 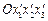, путем проектирования вектора напряжений в первоначальных осях на направления осей со штрихами.

Решение. Из отношений и следует, что вектор напряжения на координатных площадках в системе 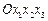имеет вид:

, , ,

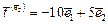что соответствует строкам тензора напряжений. Проектируем эти векторы на оси системы 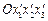при помощи соотношения 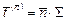, т.е.

получаем

,

,

.

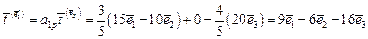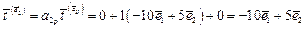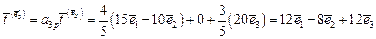Преобразуем единичные базисные вектора :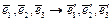

, , .

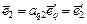В результате проекции вектора напряжений в системе 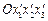имеют вид:

,

.

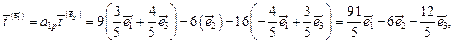
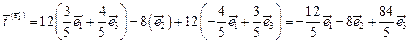Т.к. вектор напряжения на координатных площадках в системе 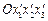соответствует строкам тензора напряжений на этих площадках, запишем .

Проверим полученный результат формулой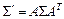

Пример 2.2. В системе осей без штрихов тензор напряжений дан в виде

.

Определить тензор напряжений в осях со штрихами, направления которых указаны на рис.2.4.

Решение. Заполним таблицу преобразований косинусами известных углов

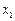
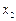
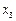
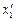
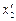
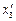
Угол b и недостающие элементы таблицы преобразования можно определить из условия ортогональности компонент матрицы А - и .

Из второго условия при i = k =1 имеем:

т.е. (со знаком «+» т.к. из рис.2.4. очевидно, что угол b острый). Таким образом матрица преобразований приняла вид:

.

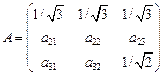Компоненту 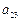найдем из условия при j=k =3:

.

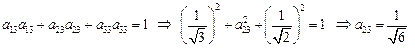Для нахождения оставшихся компонент воспользуемся условиями :

при j=k =2, ,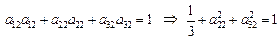

при j =2, k =3, .

Получили систему .

Разрешая систему относительно 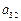, получаем следующие значения 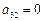и (из рис.2.4 очевидно, что 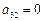постороннее решение). Из второго уравнения системы .

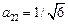Для недостающих компонент 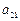и 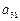используем условия 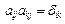при i =1, k =2 и i =1, k =3

Откуда , .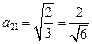

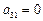Матрица преобразований имеет вид: .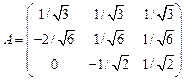

Компоненты тензора напряжений 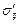в системе координат 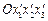находим по формуле .

,

.

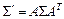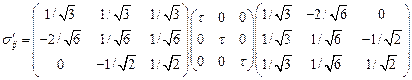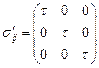Пример 2.3. Определить форму поверхности напряжения для точки среды, где компоненты тензора напряжений в ортогональной декартовой системе координат следующие: , при 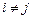(напряженное состояние самого общего вида в главных осях тензора напряжений). Исследовать вид поверхности напряжений в зависимости от знаков А, В, С.

Решение. Уравнение поверхности напряжений в символической записи имеет вид

.

Используя матричную форму получаем:

,

.

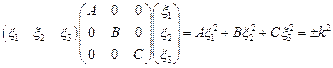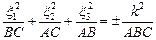Исследуем вид поверхности в зависимости от вида коэффициентов А, В, С:

1) если А, В, С имеют одинаковые знаки, то данная поверхность является эллипсоидом ;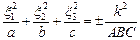

2) если А = В = С, то данная поверхность есть сфера ;

3) если А >0, ВС <0, то данная поверхность будет гиперболоидом 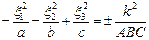или .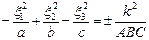

Пример 2.4. В точке тела имеется следующая система напряжений: 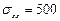кг/см², кг/см², кг/см², 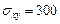кг/см², 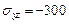кг/см², 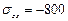кг/см². Определить значения полного нормального и касательного напряжений на площадке с заданной внешней нормалью 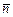, направляющие косинусы которой, относительно координатных осей, равны между собой.

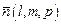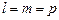Решение. Пусть вектор внешней нормали имеет вид . Для направляющих косинусов должно выполняться соотношение . Т.к. по условию , то имеем 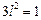Þ 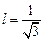. Следовательно, вектор нормали для заданной площадки имеет координаты 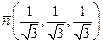. Найдем вектор напряжения: .

Нормальное напряжение находится по формуле

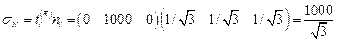кг/см².

Полное напряжение

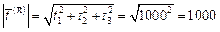кг/см².

Касательное напряжение

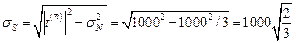кг/см².

Ответ: 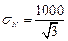кг/см², кг/см², кг/см².

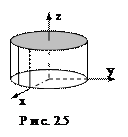Пример 2.5. Пусть в находящемся в равновесии цилиндрическом стержне, на который действуют только силы, приложенные на его торцах, во всех точках выполнены равенства . Ортогональные декартовы оси 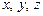выбраны так, как показано на рисунке. Показать, что:

a) существует функция напряжения 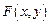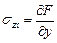, , 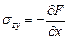введение которой приводит к удовлетворению всех уравнений равновесия;

b) условие 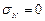на боковой поверхности стержня сводится к условию 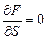вдоль контура поперечного сечения в плоскости , где S - длина дуги контура;

c) если в стержне имеется указанное выше напряженное состояние, то главный вектор сил, действующих в любом поперечном сечении, равен нулю, а главный момент сил, действующих на сечение, сводится к крутящему моменту.

Решение: а). Покажем, что введенная функция 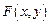удовлетворяет уравнению равновесия, которое при отсутствии поверхностных сил имеет вид или с учетом нулевых компонент тензора напряжений 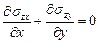Þ Þ 0=0.

b). На боковой поверхности 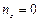Þ . Т.к. 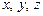ортогональная система координат, то 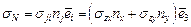, где рассматриваются как компоненты нормали к контуру поперечного сечения стержня. Т.к. 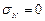, имеем или 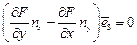. Введем единичный вектор , касательный к этому контуру. Тогда , .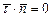

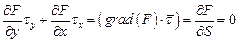Т. е. 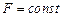на контуре поперечного сечения.

с). Используя формулу Стокса

,

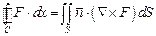где 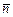- единичный вектор нормали к поверхности S рис.2.6, а dS элемент поверхности и учитывая, что 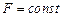на контуре сечения, получим:

, , , , .

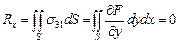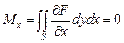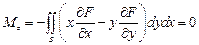Задания для самостоятельного решения по теме

«Законы преобразования напряжений. Поверхности напряжений»

Дата добавления: 2014-11-06