Кинематика. Прямолинейное движение. Криволинейное движение

Лекция 1

Основы кинематики

1.1. Прямолинейное равномерное движение

Механическое движение и его виды. Основная задача механики и способы ее решения в кинематике. Физическое тело и материальная точка. Тело отсчета. Система отсчета. Относительность механического движения. Радиус-вектор. Траектория. Путь и перемещение. Поступательное движение. Прямолинейное равномерное движение. Вектор скорости. Графическое представление движения.

1.2. Прямолинейное неравномерное движение

Неравномерное движение. Скорость при неравномерном движении. Средняя скорость. Мгновенная скорость. Ускорение. Равнопеременное движение. Равноускоренное прямолинейное движение. Равнозамедленное прямолинейное движение. Координата, путь, перемещение и скорость при равнопеременном движении. Связь между перемещением и скоростью. Относительность движения. Классический закон сложения скоростей. Графики зависимости кинематических величин от времени при равнопеременном движении. Свободное падение тел. Ускорение свободного падения.

1.3. Криволинейное движение

Перемещение и скорость при криволинейном движении. Вращательное движение. Движение по окружности с постоянной по модулю скоростью. Угол поворота. Угловая скорость. Линейная скорость. Связь угловой скорости с линейной скоростью. Ускорение при равномерном движении по окружности. Период и частота вращения.

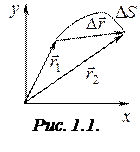Закон движения – это уравнение, которое определяет в любой момент времени положение тела, движущегося в заданной системе координат.

Положение точки в пространстве определяется координатам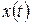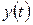и , и 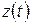или радиус-вектором 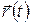(см. рис. 1.1):

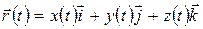, (1.1)

где векторы 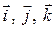показывают направление осей 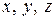соответственно.

Вектор 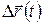, проведенный из начального положения точки в конечное (приращение радиус-вектора), равняется перемещению материальной точки:

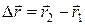. (1.2)

Длина траектории (линии, вдоль которой движется точка) 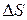– путь.

Средняя скорость материальной точки:

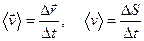. (1.3)

Среднее ускорение материальной точки:

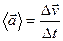. (1.4)

В случае поступательного равномерного движения уравнения можно записать

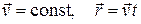, (1.5)

а в случае поступательного равнопеременного движения уравнения приобретают вид

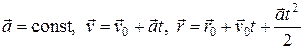. (1.6)

Закон сложения скоростей Галилея:

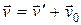, (1.7)

где 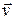– скорость материальной точки в условно неподвижной системе координат (абсолютная скорость), 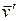– скорость материальной точки в подвижной системе координат (относительная скорость), 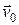– скорость подвижной системы координат относительно неподвижной.

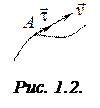Если точка 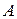(рис. 1.2) движется вдоль кривой, тогда ее положение в каждый момент времени определяется выражением

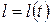, (1.8)

где 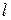– длина дуги. Линейная скорость в каждой точке 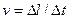направлена по касательной к кривой, тогда вектор скорости

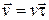, (1.9)

где 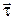– единичный вектор касательной к кривой в каждой точке.

Ускорение по определению

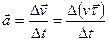. (1.10)

При криволинейном движении точки полное ускорение 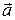– это векторная сумма тангенциального (касательного) 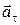и нормального (центростремительного) 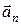ускорений:

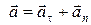. (1.11)

Модуль полного ускорения равняется:

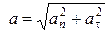, (1.12)

при этом

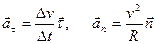, (1.13)

где 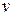– скорость тела, а 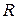– радиус кривизны траектории тела в данной точке, 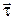– орт вектора скорости, 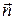– единичный вектор, направленный по нормали к траектории движения к центру кривизны траектории.

Угловая скорость тела – это приращение угла поворота тела к промежутку времени, за которое оно произошло:

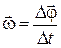. (1.14)

Направление вектора 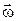находится по правилу правого винта.

Угловое ускорение 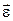– это приращение угловой скорости к промежутку времени, за которое оно произошло:

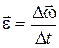. (1.15)

При равномерном вращательном движении 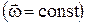выполняется соотношение:

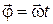. (1.16)

Связь между угловыми и линейными величинами имеет вид:

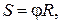(1.17)

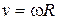, (1.18)

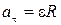, (1.19)

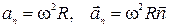, (1.20)

где 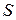– путь, который прошла точка при вращательном движении (длина дуги), 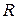– расстояние точки от оси вращения (радиус дуги).

Угловая скорость точки, которая равномерно вращается вокруг оси, связана с количеством оборотов за секунду (частотой) 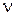и периодом вращения 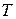соотношением:

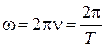. (1.21)

Дата добавления: 2014-11-06