ДИНАМИКА. 2.1. Законы движения Ньютона

Лекция 3

Основы динамики

2.1. Законы движения Ньютона

Взаимодействие тел. Инертность. Масса. Сила. Единицы измерения массы и сил. Первый закон Ньютона. Инерция. Инерциальные системы отсчета. Виды сил. Сложение сил. Равнодействующая сила. Второй закон Ньютона. Третий закон Ньютона. Принцип относительности Галилея.

2.2. Силы в природе. Применение законов динамики

Гравитационные силы. Сила всемирного тяготения. Закон Всемирного тяготения. Гравитационная постоянная. Сила тяжести. Вес тела. Невесомость. Перегрузка. Вес тела, движущегося с ускорением. Движение тела под действием силы тяжести. Свободное падение. Ускорение свободного падения. Искусственные спутники Земли. Первая космическая скорость.

Деформация. Сила упругости. Движение под действием силы упругости. Закон Гука.

Сила трения. Трение покоя. Сила трения скольжения. Трение качения. Коэффициент трения. Движение тел под действием нескольких сил.

2.3. Элементы статики

Равновесие тел с закрепленной осью вращения. Плечо силы. Момент силы. Правило моментов. Центр тяжести. Рычаг. Условие равновесия рычага. Пара сил. Виды равновесия тел. Блоки.

Основное уравнение динамики:

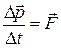, (2.1)

где 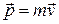– импульс, 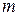– масса и 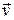– скорость тела, – изменение импульса за промежуток времени 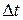, – равнодействующая всех внешних сил, на него действующих. Когда масса не изменяется, основное уравнение поступательного движения записывается в виде (второй закон Ньютона)

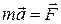, (2.2)

где 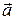– ускорение тела.

Поступательное движение системы частиц как целого можно характеризовать движением одной точки – центра масс системы:

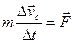, (2.3)

где – суммарная масса всех частиц рассматриваемой системы, – равнодействующая всех внешних сил, действующих на систему, 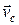– скорость движения центра масс системы.

Радиус-вектор, который определяет положение центра масс системы частиц в пространстве относительно любой точки :

, (2.4)

где – масса 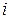-ой частицы, – ее радиус-вектор относительно точки .

Сила трения скольжения:

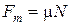, (2.5)

где 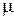– коэффициент трения скольжения, 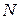– сила нормальной реакции опоры.

Сила упругости 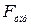, возникающая при деформации тела, пропорциональна удлинению тела и направлена в сторону, противоположную направлению перемещений частиц тела при деформации (закон Гука):

где – коэффициент пропорциональности.

Импульс замкнутой системы равняется векторной сумме импульсов ее отдельных частиц

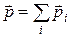. (2.6)

Две материальные точки (два однородных шара) притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними (между их центрами) (закон всемирного тяготения):

, (2.7)

где G = 6,67·10^-11 Н·м²/кг² – гравитационная постоянная. Если тело массой m находится над поверхностью Земли на высоте h, то на него действует сила земного притяжения, равная по модулю

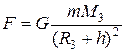. (2.8)

Составляющую силы земного притяжения по отвесному направлению в данной точке земного шара, равную 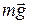, называют силой тяжести, а ускорение , создаваемое этой силой, – ускорением свободного падения. Ускорение свободного падения не зависит от массы тела. Если не учитывать вращение Земли и считать ее шаром, то и, следовательно,

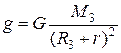. (2.9)

Если тело находится на поверхности Земли или на близком от нее расстоянии (), то

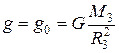(2.10)

и можно считать, что ускорение свободного падения имеет для всех тел не только одинаковое, но и постоянное значение.

Из соотношений (2.9) и (2.10) следует, что

.

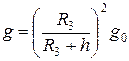Весом тела называют силу, с которой тело действует на горизонтальную опору или подвес, удерживающие его от свободного падения. Следует иметь в виду, что по модулю вес и сила тяжести могут сильно отличаться друг от друга, как, например, при невесомости (или перегрузке), и отождествление их приводит к абсурду.

Давлением называют скалярную физическую величину, равную отношению модуля силы 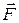, действующей перпендикулярно участку поверхности и равномерно распределенной вдоль него, к площади S этого участка:

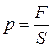. (2.11)

Если сила 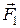направлена так, что угол между нею и нормалью к поверхности равен α, то давление

.

Если внутри покоящейся жидкости расположить в окрестности некоторой точки А небольшую площадку площадью S, то на нее со стороны жидкости будет действовать сила ; при этом давление не зависит от ориентации площадки. Именно это имеют в виду, когда говорят, что давление в жидкости одинаково по всем направлениям. В пределе, при стремлении Δ S к нулю, говорят о давлении в данной точке жидкости. Давление является характеристикой состояния жидкости в данном месте и не зависит от площади Δ S и ориентации площадки.

Сила гидростатического давления жидкости на дно сосуда равна весу столба жидкости с основанием, равным площади дна сосуда:

.

Давление р ₀ на открытой поверхности жидкости передается во все точки жидкости без изменения (закон Паскаля).

Из закона Паскаля следует:

1) полное давление в любой точке жидкости складывается из давления р₀ на ее открытой поверхности и гидростатического давления столба жидкости, находящегося над этой точкой:

; (2.12)

2) при равновесии жидкости давление на поверхности одного уровня внутри однородной жидкости во всех точках этой поверхности одинаково.

Пусть, например, в открытом сосуде находится жидкость. Давление на ее поверхность, производимое атмосферным воздухом, передается, согласно закону Паскаля, во все точки жидкости. На глубине h ₁ в этой жидкости давление равно сумме атмосферного давления р ₀ и давления, создаваемого весом столба жидкости высотой h ₁ (гидростатического давления). По формуле (2.12)

,

где ρ – плотность жидкости; g – ускорение свободного падения. На глубине давление

.

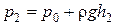На тело, погруженное в жидкость, действует выталкивающая сила, модуль которой равен весу жидкости, вытесненной телом (сила Архимеда):

, (2.13)

где ρ _ж – плотность жидкости; V – объем вытесненной жидкости. Выталкивающая сила является суммой сил упругости, действующих на поверхность тела со стороны жидкости. Приложена эта сила в центре тяжести вытесненного объема жидкости и направлена по нормали к свободной поверхности жидкости.

Дата добавления: 2014-11-06