Примеры решения задач. Задача 1.6.Найти графическим способом перемещение и путь, пройденный за t1 = 5 с материальной точкой

Задача 1.6. Найти графическим способом перемещение и путь, пройденный за t ₁ = 5 с материальной точкой, движение которой вдоль оси ОХ описывается уравнением х = 6 – 4 t + t ², где все величины выражены в единицах СИ.

Решение. В задаче 1.5 мы нашли (4) проекцию скорости на ось ОХ:

.

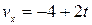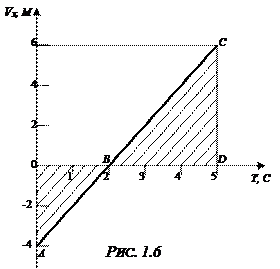Соответствующий этому выражению график скорости изображен на рисунке 1.6. Проекция перемещения на ось ОХ равна алгебраической сумме площадей треугольников АОВ и BCD. Поскольку проекция скорости на первом участке отрицательная, то площадь треугольника АОВ берем со знаком минус; а проекция скорости на втором участке положительная, то площадь треугольника BCD берем со знаком плюс:

.

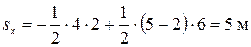Поскольку путь – это длина траектории и не может убывать, то чтобы найти его, сложим площади этих треугольников, считая при этом положительной площадь не только треугольника BCD, но и треугольника АОВ:

.

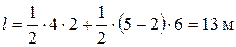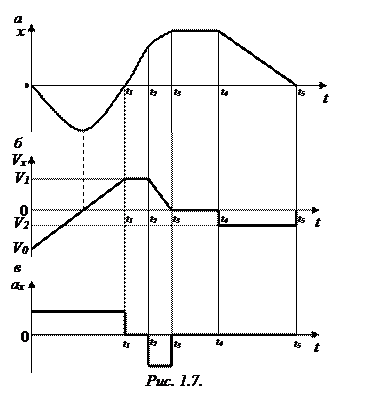Ранее (см. задачу 1.5) мы нашли этот путь другим способом – аналитически.

Задача 1.7. На рис. 1.7, a изображен график зависимости координаты некоторого тела, движущегося прямолинейно вдоль оси ОХ, от времени. Криволинейные участки графика являются частями парабол. Построить графики зависимости скорости и ускорения от времени.

Решение. Чтобы построить графики скорости и ускорения, установим по данному графику (рис. 1.7, а) характер движения тела в разные промежутки времени.

В промежутке 0 – t ₁ график координаты представляет собой часть параболы, ветви которой направлены вверх. Следовательно, в уравнении

,

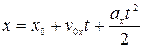выражающем в общем виде зависимость координаты х от времени t, коэффициент перед t ² положительный, т.е. а _х > 0. А так как парабола смещена вправо, то это означает, что v _{0 x} < 0, т.е. тело имело начальную скорость, направленную противоположно направлению оси ОХ. В течение промежутка 0 – t ₁ модуль скорости тела сначала уменьшается до нуля, а затем скорость меняет направление на противоположное и ее модуль увеличивается до некоторого значения v ₁. График скорости на этом участке – отрезок прямой, проходящей под некоторым углом к оси t (рис. 1.7, б), а график ускорения – отрезок горизонтальной прямой, лежащей выше оси времени (рис. 1.7, в). Вершина параболы на рис. 1.7, а соответствует значению v _{0 x} = 0 на рис. 1.7, б.

В промежутке времени t ₁ – t ₂ тело двигалось равномерно со скоростью v ₁.

В промежутке t ₂ – t ₃ график координаты – часть параболы, ветви которой направлены вниз. Следовательно, здесь а_х < 0, скорость тела убывает до нуля к моменту времени t ₃, а в промежутке времени t ₃ – t ₄ тело покоится. Затем в течение промежутка времени t ₄ – t ₅ тело движется равномерно со скоростью v ₂ в обратную сторону. В момент времени t ₅ оно достигает точки начала отсчета координат и останавливается.

Учитывая характер движения тела, построим соответствующие графики проекций скорости и ускорения (рис. 1.7, б, в).

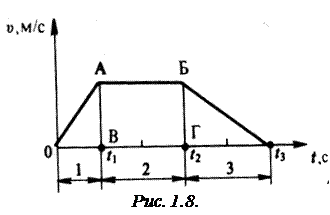
Задача 1.8. Пусть график скорости имеет вид, изображенный на рис. 1.8. Исходя из этого графика, нарисуйте график зависимости пути от времени.

Решение. Разделим весь рассматриваемый промежуток времени на три участка: 1, 2, 3. На участке 1 тело движется равноускоренно без начальной скорости. Формула пути для этого участка имеет вид

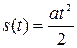, (1)

где а – ускорение тела.

Ускорение есть отношение изменения скорости к промежутку времени, за которое это изменение произошло. Оно равно отношению отрезков .

На участке 2 тело движется равномерно со скоростью v, приобретенной к концу участка 1. Равномерное движение началось не в начальный момент времени, а в момент t ₁. К этому моменту тело уже прошло путь 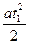. Зависимость пути от времени имеет для участка 2 следующий вид:

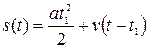. (2)

На участке 3 – движение равнозамедленное. Формула пути для этого участка выглядит следующим образом:

,

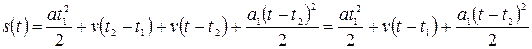где а ₁ – ускорение на участке 3. Оно вдвое меньше ускорения а на участке 1, поскольку участок 3 вдвое длиннее участка 1.

Сделаем выводы. На участке 1 график пути имеет вид параболы, на участке 2 – прямой линии, на участке 3 – тоже параболы, но перевернутой (с выпуклостью, обращенной вверх) (см. рис. 1.9).

График пути не должен иметь изломов, он изображается плавной линией, т. е. параболы сопрягаются с прямой линией. Это объясняется тем, что тангенс угла наклона касательной к оси времени определяет значение скорости в момент времени t, т.е. по наклону касательных к графику пути можно найти скорость тела в тот или иной момент времени. А поскольку график скорости непрерывен, то из этого следует, что график пути не имеет изломов.

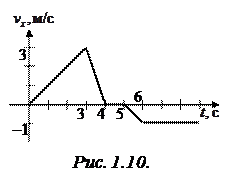Кроме того, вершина перевернутой параболы должна соответствовать моменту времени t ₃. Вершины парабол должны соответствовать моментам 0 и t ₃, так как в эти моменты скорость тела равна нулю и касательные к графику пути должны быть для этих точек горизонтальными.

Путь, пройденный телом за время t ₂, численно равен площади фигуры ОАБГ, образуемой графиком скорости на промежутке Оt ₂.

Задача 1.9. На рис. 1.10 изображен график зависимости проекции скорости некоторого тела, движущегося прямолинейно вдоль оси ОХ, от времени. Построить графики зависимости ускорения, координаты и пути 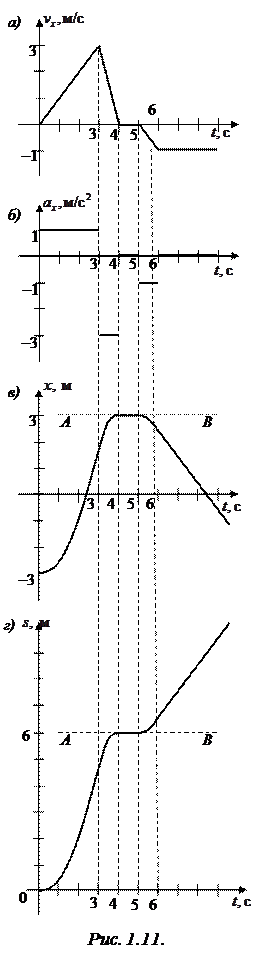от времени. В начальный момент времени тело находилось в точке х ₀ = –3 м. Все величины заданы в единицах СИ.

Решение. Чтобы построить график зависимости ускорения а_х (t), определим по графику v_х (t) характер движения тела в разные промежутки времени. Вспомним, что по определению

,

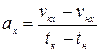где проекция скорости , .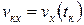

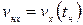В промежутке времени [0; 3] c:

.

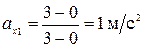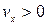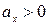На этом участке и (знаки одинаковые), т.е. тело движется равноускоренно.

В промежутке времени [3; 4] c:

,

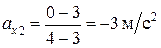т.е. 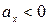и 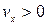(знаки проекций противоположные) – движение равнозамедленное.

На участке [0; 4] c проекция скорости 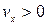, т.е. движение происходит в положительном направлении оси ОХ.

На участке [4; 5] c проекция скорости 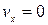– тело покоится (и ).

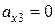На участке [5; 6] c:

.

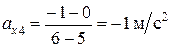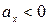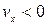и (знаки одинаковые) – движение равноускоренное, но т.к. 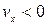, то тело движется против оси ОХ.

После шестой секунды 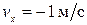, тело движется равномерно (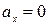) против оси ОХ.

График а_х (t) изображен на рис. 1.11, б.

Уравнение 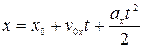в общем виде выражает зависимость координаты х от времени t. По условию х (0) = х ₀ = –3 м.

На участке [0; 3] c:

,

.

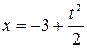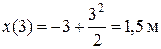График х (t) на этом участке – парабола, ветви которой направлены вверх, а вершина расположена в точке t = 0 c (здесь ).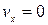

На участке [3; 4] c:

.

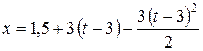График х (t) на этом участке – парабола, ветви которой направлены вниз, а вершина расположена в точке t = 4 с (здесь ).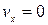

.

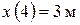На участке [4; 5] c тело покоится, т.е. координата 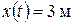не изменяется.

На участке [5; 6] с:

.

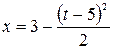График – парабола, ветви которой направлены вниз, а вершина находится в t = 5 с ().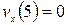

.

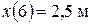После 6 с тело движется равномерно.

.

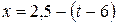График движения – прямая линия. Для построения графика 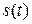– пути от времени, надо учесть, что 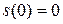и путь, в отличие от координаты, не может уменьшаться. Т.е. для построения 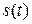график надо сдвинуть вверх и после t = 5 с зеркально отразить относительно горизонтальной прямой АВ.

За первые 3 с тело прошло 4,5 м, за следующую секунду – 1,5 м, потом 1 с покоилось, затем за промежуток времени [6; 7] с прошло 0,5 м, а дальше каждую секунду проходило 1 м, т.е. график 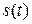выглядит, как представлено на рис. 1.11, г.

Дата добавления: 2014-11-06