Амплитудная модуляция

Амплитудные модуляторы производят преобразования вида

Процесс амплитудной модуляции состоит в преобразовании

“медленного” сигнала S (t), называемого модулирующим, в быстро осциллирующий сигнал, амплитуда которого меняется по закону S (t):

.

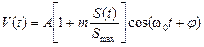Здесь A cos w ₀t - функция, называемая несущим колебанием, m - коэффициент модуляции (m ≤1), где ; S _max=max| S (t)|, где S (t) – информационная функция.

Например, если S (t) - модулирующий сигнал, то соответствующий ему АМ-сигнал имеет вид следующего графика.

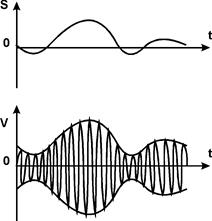
Определим спектр амплитудно-модулированного колебания.

Пусть АМ-колебание описывается функцией V (t)= f (t)cos w ₀ t. На основании прямого преобразования Фурье спектр этой функции будет содержать 2 группы гармоник: суммарной и разностной частот

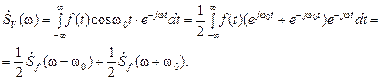
Поскольку по определению в выражении

есть спектр функции 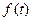, то последняя формула означает, что при АМ-модуляции спектр НЧ - колебания переносится в область ВЧ - колебания и раздваивается.

В нашем случае

, где .

Спектр такой функции состоит из двух частей:

.

Следовательно, на основании предыдущей формулы спектр АМ-колебания будет иметь вид

.

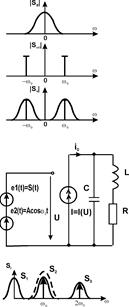
На приведенном ниже рисунке изображены спектры модулирующего сигнала, несущего и АМ-колебания. Как видно, в результате модуляции спектр информационного сигнала переносится в область несущего колебания.

Процесс амплитудной модуляции является типичным преобразованием спектра сигнала S (t) и может быть осуществлен только в цепи с нелинейным элементом. Поскольку получение АМ-колебания требует двух сигналов - модулирующего S (t) и несущего A cos w ₀ t, на нелинейный элемент должна действовать сумма этих сигналов.

Включенный последовательно с нелинейным элементом линейный полосовой фильтр (ПФ), например колебательный контур, настроенный на несущую частоту w₀, выделяет полосу частот, соответствующую АМ-колебанию.

Проанализируем эту модель. Пусть ВАХ безынерционного нелинейного элемента описывается многочленом второй степени

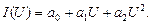
Определим входной ток полосового фильтра:

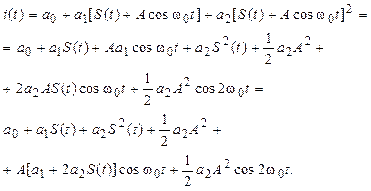
Рассмотрим спектральный состав тока, полагая, что резонансная частота контура w ₀ много больше максимальной частоты w _max в спектре S (t). НЧ - спектр S ₁ обусловлен постоянной составляющей и членами с S (t) и S ²(t), а спектры S ₂ и S ₃ образуются сигналами, пропорциональными cos w ₀ t и cos2 w ₀ t соответственно. Если теперь принять, что полоса пропускания полосового фильтра сосредоточена вблизи w ₀ (пунктир на графике), то он будет выделять колебание, пропорциональное cos w ₀ t, которое и представляет собой АМ-колебание.

Таким образом, АМ-колебания получаются путем нелинейного сложения сигнала модуляции S (t) и несущего колебания. В результате получается выходное напряжение следующего вида:

Практической схемой, осуществляющей процесс АМ-модуляции, является, например, следующая схема на полевом транзисторе с предварительным сложением модулирующего и несущего колебаний.

Напряжение между затвором и истоком U _ЗИ вычисляется по формуле, полученной на основании законов Кирхгофа в предположении, что :

.

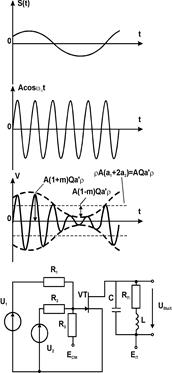
Подбором значений сопротивлений R ₁, R ₂, R ₃ и напряжения смещения Е_СМ осуществляется выбор рабочей точки на передаточной характеристике транзистора. Наилучшим считается такое положение рабочей точки, когда коэффициенты разложения ВАХ в окрестности этой точки обеспечивают максимальное значение коэффициента модуляции по первой гармонике выходного тока.

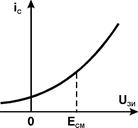
Модулированный сигнал получается как падение напряжения на колебательном контуре, параметры должны обеспечивать центральную частоту Сопротивление потерь R _П должно быть таким, чтобы добротность 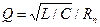цепи была достаточно большой, чтобы полоса пропускания контура 2Δ w << w ₀ (несущей частоты). С другой стороны, спектр модулированного сигнала не должен искажаться, т. е. необходимо, чтобы W _m < Δ w, где 2 W _m - ширина спектра модулирующего колебания. Используя равенство 2Δ w = w ₀/ Q, получаем неравенства для выбора параметров колебательного контура L, C, R _П:

.

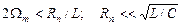Коэффициенты а ₀, а ₁, а ₂,..., определяющие вид нелинейной характеристики транзистора, зависят от выбора постоянного смещения на затворе, задаваемого сопротивлением R ₁, R ₂, R ₃ E _cм. При изменении этого напряжения будет меняться амплитуда а ₁ АQ выходного напряжения V (t). Зависимость амплитуды первой гармоники тока на выходе нелинейного элемента (или падение напряжения на колебательном контуре на первой гармонике) от поданного напряжения смещения называют статической модуляционной характеристикой.

Величину E _ОПТ, оптимальную для рабочего модулятора, выбирают в середине линейного участка статической модуляционной характеристики. Амплитуда сигнала S _max не должна выходить за пределы линейного участка модуляционной характеристики. Статическая модуляционная характеристика – это не есть проходная ВАХ транзистора.

Дата добавления: 2014-11-06