Преобразование частоты

Формирование и демодуляция радиосигналов.

Одним из важнейших свойств нелинейных цепей является преобразование спектра входных сигналов. Оно заключается в том, что при действии на входе цепи гармонического или импульсного сигнала, состоящего из суммы нескольких гармонических колебаний различных частот, реакция (т. е. ток или напряжение любой ветви) будет содержать не только гармоники воздействия, но и новые гармоники, которых нет во входном сигнале.

Такое преобразование спектра принципиально невозможно в линейных цепях с постоянными параметрами (RLC - цепях). Там токи и напряжения в любой ветви состоят только из гармоник, содержащихся во входном сигнале.

Пусть задана нелинейная резистивная цепь с передаточной (или выходной) характеристикой, заданной в виде степенного полинома. Пусть это, например, ВАХ в виде

.

Рассмотрим сначала действия на цепь гармонического сигнала:

.

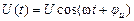Подставив второе выражение в первое, получаем

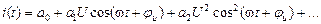
Из тригонометрии известно, что

Как видно, гармоническая функция степени n эквивалентна сумме функций кратных частот, причем четная степень содержит только четные гармоники, нечетная - только нечетные. Очевидно, что наибольшая частота гармоник, равная nw, определяется старшей степенью полинома характеристики цепи:

В общем виде можно записать:

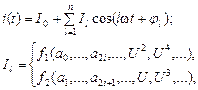
На следующем рисунке изображен дискретный спектр входного и выходного сигналов для нелинейности общего вида (а), четной (б) и нечетной (в) функций i (U).

Рассмотрим теперь действие на цепь сигнала, состоящего из суммы двух гармонических функций с частотами w ₁ и w ₂:

.

Реакция цепи будет состоять из суммы степеней двучленов:

.

При n =2, 3 степени двучленов будут такими:

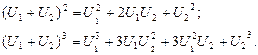
В отличие от воздействия одного сигнала при воздействии сигнала в виде суммы двух функций в отклике имеются еще и дополнительные слагаемые в виде произведения степеней (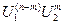), где m =1,2,..., n. При этом все степени гармонических функций дают суммы гармоник кратных частот.

Произведения двух гармонических функций дают гармонические функции с частотами, равными разностям и суммам частот сомножителей. В качестве первого приближения можно записать:

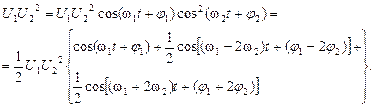
Таким образом, в произведении степеней имеем в общем случае частоты w _mn=± m w ₁± n w ₂, m =1, 2,..., n. Колебания с частотами w _mn называются комбинационными, а сумма - порядком комбинационного колебания.

Спектр сигнала на выходе безынерционного нелинейного четырехполюсника в случае действия на его входе суммы двух гармонических сигналов приведен на следующем рисунке.

Таким образом, в общем случае при действии суммы двух гармонических сигналов отклик цепи содержит колебания комбинационных частот

Появление в спектре выходного сигнала нелинейного элемента составляющих, которых не было во входном сигнале, широко используют в технике.

Важнейшими применениями этого явления являются умножение частоты, модуляция и детектирование (демодуляция). Во всех устройствах, в которых производятся эти преобразования, нелинейные элементы используются совместно с линейными цепями - фильтрами.

Дата добавления: 2014-11-06