Графический метод анализа стационарного режима

Понятие колебательной характеристики нелинейной цепи позволяет определить стационарную амплитуду в цепи с обратной связью графическим методом.

По определению, колебательная характеристика есть зависимость амплитуды первой гармоники выходного тока I ₁ нелинейного элемента от амплитуды U входного гармонического напряжения. Поэтому для графического решения уравнения баланса амплитуд необходима характеристика обратной связи, представляющая собой зависимость амплитуды напряжения обратной связи U от амплитуды тока I ₁. Поскольку цепь обратной связи линейная, искомая зависимость

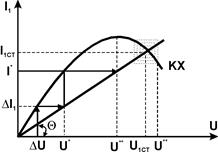
представляет собой прямую линию, проходящую через начало координат. Угол наклона ее зависит от способа реализации обратной связи. В нашем случае 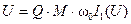и - угол между осью абсцисс и прямой обратной связи. Графики будут иметь две точки пересечения - начало координат и некоторую точку U_CT, I_CT. Эти точки соответствуют двум возможным стационарным состояниям цепи: первая - отсутствию колебаний, вторая - стационарным автоколебаниям с амплитудой U _CT. Покажем, что первая точка является неустойчивой. Пусть имеется небольшая начальная флуктуация DU. Ей будет соответствовать появление тока с амплитудой первой гармоники DI ₁. Этот ток создает в цепи обратной связи напряжение U^*, которое приведет к появлению тока I^* и т. д. Таким образом, малая начальная флуктуация DU приведет к установлению стационарной ненулевой амплитуды колебаний.

Для того, чтобы нулевая точка была неустойчивой, прямая обратной связи должна проходить в начале координат ниже графика колебательной характеристики:

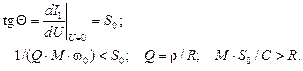
Это условие самовозбуждения было уже получено из анализа корней характеристического многочлена дифференциального уравнения цепи.

Рассмотренная цепь считается находящейся в мягком режиме самовозбуждения, когда колебания возникают при . Очевидно (из построений), что точка U_СТ, I_СТ является устойчивой, поскольку любые DU приводят к ее возврату в прежнее положение.

Расположение линии обратной связи по отношению к колебательной характеристике может быть и иным. В этом случае стационарный режим будет при нулевой амплитуде. В цепи не возникает автоколебаний при любых отклонениях DU.

Если график колебательной характеристики I₁(U) имеет S - образную форму, то начальная точка будет устойчивой, однако цепь может самовозбудиться, если в ней возникнет начальная флуктуация DU>U_пор. Режим, когда начальная точка является устойчивой, но существует пороговое значение флуктуаций, превышение которого приводит к самовозбуждению, называется жестким режимом возбуждения генератора.

Таким образом, нелинейная цепь может вести себя по-разному при малых и сильных внешних воздействиях. Если по линеаризованному дифференциальному уравнению можно установить устойчивость или неустойчивость цепи “в малом”, то анализ колебательной характеристики совместно с прямой обратной связи позволяет провести анализ устойчивости “ в большом” и определить возможность существования жесткого режима возбуждения.

Метод гармонической линеаризации пригоден для анализа цепей с узкополосными фильтрами - колебательными контурами с высокой добротностью. Если же фильтр не является таким контуром, то автоколебания будут возникать не только на первой гармонике, но и на других (w = nw ₀). При этом форма колебаний будет негармонической. Для анализа процессов в таких цепях используют метод уравнений состояния и их численное интегрирование.

Дата добавления: 2014-11-06