Теоретическая часть

1. ПОНЯТИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА И ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ

Рассмотрим задачу о нахождении площади криволинейной трапеции.

Пусть дана некоторая функция y=f(x), график которой изображён на рисунке.

Рис 1. Геометрический смысл определенного интеграла.

На оси 0х выберем точки “ a” и “в” и восстановим из них перпендикуляры до пересечения с кривой. Фигура ограниченная кривой, перпендикулярами и осью 0х называется криволинейной трапецией. Разобьём интервал на ряд небольших отрезков. Выберем произвольный отрезок 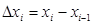. Достроим криволинейную трапецию, соответствующую этому отрезку до прямоугольника. Площадь такого прямоугольника определится как:

.

Тогда площадь всех достроенных прямоугольников в интервале будет равна:

;

Если каждый из отрезков достаточно мал и стремится к нулю, то суммарная площадь прямоугольников будет стремиться к площади криволинейной трапеции:

;

Итак, задача о вычислении площади криволинейной трапеции сводится к определению предела суммы.

Интегральная сумма есть сумма произведений приращения аргумента на значение функции f(x), взятой в некоторой точке интервала, в границах которого изменяется аргумент. Математически задача о нахождении предела интегральной суммы, если приращение независимой переменной стремится к нулю, приводит к понятию определённого интеграла.

Функция f(x ) в некотором интервале от х=а до х=в интегрируема, если существует такое число, к которому стремится интегральная сумма при Dх®0. В этом случае число J называют определённым интегралом функции f(x) в интервале :

;

где ] а, в [ – область интегрирования,

а –нижний предел интегрирования,

в –верхний предел интегрирования.

Таким образом, с точки зрения геометрии, определённый интеграл есть площадь фигуры, ограниченной графиком функции в определённом интервале ] а, в [ и осью абцисс.

2. СВЯЗЬ МЕЖДУ ОПРЕДЕЛЁННЫМ И НЕОПРЕДЕЛЁННЫМ ИНТЕГРАЛАМИ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА

Неопределённый интеграл - это совокупность первообразных функций. Определённый интеграл - это число. Связь между ними задаётся формулой Ньютона-Лейбница.

Теорема. Значение определённого интеграла равно разности значений любой первообразной от подинтегральной функции, взятой при верхнем и нижнем пределами интегрирования:

Например: .

3. СВОЙСТВА ОПРЕДЕЛЁННОГО ИНТЕГРАЛА

1. Определённый интеграл не зависит от обозначения переменной интегрирования:

;

2. Определённый интеграл от алгебраической суммы конечного числа непрерывных функций , заданных на отрезке равен алгебраической сумме определённых интегралов от слагаемых функций:

;

3. Постоянный множитель можно вынести за знак интеграла:

;

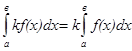4. Если верхний и нижний пределы интегрирования поменять местами, то определённый интеграл изменит свой знак на противоположный:

;

5. Если а=в, то ;

6. Если отрезок интегрирования разбить на две части и , то:

;

7. Если подинтегральная функция на отрезке интегрирования сохраняет постоянный знак, то интеграл представляет собой число того же знака, что и функция, т.е. если 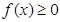, то

;

8. Значение определённого интеграла заключено между произведениями наибольшего и наименьшего значений подинтегральной функции на длину интервала интегрирования:

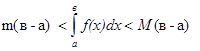, где M,m – наибольшее и наименьшее значения функции на отрезке : m £ £ M.

9. Определённый интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке х=С отрезка интегрирования на длину отрезка (в-а):

,

где f(c) - среднее значение функции в интервале.

4. ОСНОВНЫЕ МЕТОДЫ НАХОЖДЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА

Дата добавления: 2014-10-15