По уровню дохода в апреле 2003 г

По тарифным разрядам

Распределение рабочих бригады слесарей цеха № 3

Производственных фондов и среднесписочной численности работников.

Группировка предприятий по величине стоимости основных

Группы предприятий по стоимости основных про-изводственных фондов, млн. руб.	в том числе подгруппы по ср,списочной численности работающих, чел.	Число предприя-тий	Основные производствен-ные фонды, млн. руб.	Число работников, чел.	Объем продукции, млн. руб.
10-22	200-290
	290-380
	380-470	-	-	-	-
	470-550	-	-	-	-
	свыше 550	-	-	-	-
Итого:
22-34	200-290
	290-380
	380-470
	470-550	-	-	-	-
	свыше 550
Итого:
34-46	200-290	-	-	-	-
	290-380
	380-470
	470-550	-	-	-	-
	свыше 550	-	-	-	-
Итого:
46-58	200-290	-	-	-	-
	290-380
	380-470
	470-550
	свыше 550	-	-	-	-
Итого:
58-70	200-290
	290-380	-	-	-	-
	380-470
	470-550	-	-	-	-
	свыше 550
Итого:
Всего

Результаты сводки и группировки могут быть представлены в виде статистических рядов распределения.

Статистическим рядом распределения называют упорядоченное распределение единиц совокупности на группы по изучаемому признаку. В зависимости от признака ряды могут быть вариационные (количественные) и атрибутивные (качественные).

Атрибутивными называют ряды распределения, построенные по качественным признакам, т.е. не имеющим числового выражения.

Примером атрибутивного ряда распределения может служить распределение студентов группы 2255 по полу (табл.1.7).

Таблица 1.7

Распределение студентов группы 2255

экономического факультета ВТУЗа

Группы студентов по полу	Число студентов, чел.	Удельный вес в общей численности студентов, %
Женщины		63,3
Мужчины		36,7
Всего:		100,0

Вариационными рядами называют ряды распределения, построенные по количественному признаку. Вариационные ряды могут быть дискретными или интервальными.

Дискретный ряд распределения – это ряд, в котором варианты выражены целым числом. Примером такого ряда может служить распределение рабочих по тарифным разрядом (табл.1.8).

Таблица 1.8

Тарифный разряд	Число рабочих, чел.
Итого:

Интервальный ряд распределения – это ряд, в котором значения признака заданы в виде интервала. Примером такого ряда может служить распределение работников ремонтно-строительной фирмы «Вега» по уровню дохода (табл.1.9).

Таблица 1.9

Распределение работников ремонтно-строительной фирмы «Вега»

Группы работников по уровню дохода, руб.	Число работников, чел.	Удельный вес, % к итогу
1000-3000		21,0
3000-5000		31,6
5000-7000		26,3
7000-9000		15,8
9000 и более		5,3
Итого:		100,0

Правила построения рядов распределения аналогичны правилам построения группировок. При определении интервальных рядов распределения необходимо определить, какое число групп следует образовать и какие взять интервалы (равные, неравные, закрытые, открытые).

РАЗДЕЛ 2. СРЕДНИЕ ВЕЛИЧИНЫ

Методические указания и решение типовых задач

Средние величины в статистике выполняют роль обобщающих показателей, характеризующих изучаемую совокупность единиц по какому-либо признаку.

При изучении вопроса о применении средних особое внимание следует обратить на то, что каждый вид средней определяется в зависимости от конкретного экономического условия и от поставленной задачи. В противном случае средняя даст ошибочный результат и будет являться искаженной характеристикой изучаемой статистической совокупности. Следует уяснить, что средняя рассчитывается по качественно однородной совокупности, значения которой примерно одного порядка. Это основное условие применения средней.

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.

В статистическом анализе используют следующие виды средних величин:

• средняя арифметическая простая;
• средняя арифметическая взвешенная;
• средняя гармоническая;
• средняя геометрическая;
• структурные средние: мода и медиана.

Средняя арифметическая простая применяется в случаях, когда имеются отдельные значения признака, т.е. данные не сгруппированы.

Средняя арифметическая простая рассчитывается по формуле:

где X – значение показателя;

n - число значений.

Пример 1. Имеются данные о выпуске продукции рабочими за смену:

№ рабочего
Количество изготовленных деталей, шт.

Необходимо определить среднюю выработку рабочего за смену.

В данном случае применима средняя арифметическая простая:

Таким образом, средняя выработка деталей на одного рабочего за смену составляет 18,4 шт.

Средняя арифметическая взвешенная применяется в том случае, когда имеется некоторая повторяемость значений единиц совокупности. Средняя арифметическая взвешенная определяется по формуле:

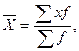
где f – частота (повторяемость признака).

Пример 2. Имеются следующие данные о возрасте студентов одной из учебных групп:

Возраст, лет	Число студентов, чел.
Всего

Определить средний возраст студентов.

Для исчисления среднего возраста воспользуемся формулу средней арифметической взвешенной. Расчеты представим в таблице 2.1.

Таблица 2.1.

Расчетная таблица для исчисления среднего возраста студентов

Возраст, лет (x)	Число студентов, чел .(f)	xf
Итого:

года

Таким образом, средний возраст студентов одной из учебных групп составляет 19,4 года.

Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или открытыми интервалами. Рассмотрим расчет средней арифметической для таких рядов.

Пример 3. Распределение промышленных предприятий региона по показателю затрат на 1 тыс. руб. продукции в октябре 2003 следующее:

Затраты на 1 тыс. руб. продукции, руб.	Число предприятий
600-650
650-700
700-750
750-800

Необходимо определить средний размер затрат на 1 тыс. руб. продукции по предприятиям региона.

В данном ряду варианты осредняемого признака (затраты на 1 тыс. руб. продукции) представлены не одним числом, а виде интервала «от – до».

Исчисление средней величины по сгруппированным данным производится по формуле средней арифметической взвешенной. Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так, для первой группы дискретная величина х будет равна:

и т.д.

Дальнейший расчет производится обычным методом определения средней арифметической взвешенной. Все необходимые расчеты представлены в таблице 2.2.

Таблица 2.2

Расчетная таблица для определения среднего размера затрат на 1 тыс. руб. продукции по предприятиям региона в октябре 2003 г.

Затраты на 1 тыс. руб. продукции, руб.	Число предприятий (f)	Середина интервала (x)	xf
600-650
650-700
700-750
750-800
Итого:		-

Средний размер затрат на 1 тыс. руб. продукции по предприятиям региона равен:

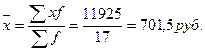
Рассмотрим другой случай исчисления средней величины в ряду распределения с открытыми интервалами.

Пример 4. Имеются следующие данные о распределении работников предприятия по возрасту:

Возраст, лет	Число работников, чел.
до 25
25-30
30-40
40-50
50-60
50-60
60 и более

Необходимо рассчитать средний возраст работников предприятия.

Распределение работников по возрасту представляет собой интервальный ряд распределения, открытый (нет крайних значений).

В этом случае за х принимаем серединное значение интервалов. Величину первого интервала условно приравниваем к величине второго, тогда его нижняя граница будет равна 20 лет. Величину последнего интервала условно приравниваем к величине предпоследнего, тогда верхняя граница составит 70 лет. В результате получаем следующие середины интервалов:

(20 + 25): 2 = 22,5;

(25 + 30): 2 = 27,5;

(30 + 40): 2 = 35,0;

(40 + 50): 2 = 45,0;

(50 + 60): 2 = 55,0;

(60 + 70): 2 = 65,0

Для расчета среднего возраста работников предприятия воспользуемся формулой средней арифметической взвешенной:

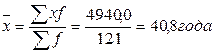
Все необходимые расчеты для исчисления средней величины представлены в таблице 2.3.

Таблица 2.3

Расчетная таблица для определения

Дата добавления: 2014-11-06