Затрат на 1 тыс.руб.продукции в октябре 2003 г

Распределение промышленных предприятий региона по показателю

Затраты на 1 тыс. руб. продукции, руб.	Число предприятий (f)	Накопленные частоты (S)
600-650
650-700
700-750
750-800
Итого:

В этом примере наибольшее число предприятий (7) имеет затраты на 1 тыс. руб. продукции от 650 до 700 руб. Следовательно, этот интервал является модальным интервалом ряда распределения. Введем следующие обозначения:

x_Mo = 650;

i_Mo = 50;

f_Mo-1 = 2;

f_Mо+1 = 5.

f_Mo = 7;

Подставим числовые значения в формулу моды и произведем вычисления: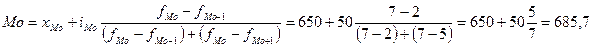

Следовательно, наибольшее число предприятий в регионе имеет затраты в размере 685,7 руб. на 1 тыс. руб. продукции.

Для нахождения медианы определим, прежде всего, медианный интервал. В данной задаче сумма накопленных частот, превышающая половину всех значений (9), соответствует интервалу 650 – 700. Это и есть медианный интервал, в котором находится медиана. Определим ее значение по приведенной выше формуле.

Известно, что:

x_Me – 600;

i_Me - 50;

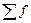- 17;

S_Me-1 – 2;

f_M - 7.

Подставим числовые значения в формулу медианы:

=

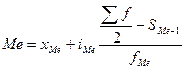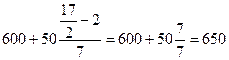
Таким образом, половина предприятий имеет затраты в размере до 650 руб. на 1 тыс. руб. продукции, остальные предприятия – более 650 руб.

В нашем случае 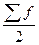= 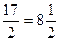. Поскольку частота не может быть дробным числом, добавляем 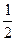, получаем целое число – 9.

РАЗДЕЛ 3. ПОКАЗАТЕЛИ ВАРИАЦИИ

Методические указания и решение типовых задач

Средняя величина дает обобщающую характеристику признака в совокупности, но она не раскрывает строение совокупности. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от средней. Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака скрывается за средними.

Исследование вариации в статистике и социально – экономических исследованиях имеет важное значение, так как величина вариации признака в статистической совокупности характеризует ее однородность.

В статистической практике для изучения и измерения вариации используются различные показатели вариации:

· размах вариации (R);

· среднее линейное (абсолютное) отклонение ();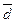

· среднее квадратическое отклонение ;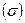

· дисперсия ;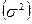

· коэффициент вариации (V).

Рассмотрим вычисление показателей вариации на примере.

Пример 1. Для определения скорости износа резцов было проведено обследование 1000 резцов. Получены следующие результаты:

Таблица 3.1

Дата добавления: 2014-11-06