
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дискретная математика
|
|
|
|
OQQ
Ньютон (Newton) И. 30, 262
Остен (Austen) Э. 162
Паскаль (Pascal) Б. 126
Пере (Pere/) 307
Пидерит (Piderit) T. 287
Платон (Platon) 141
Подан (Paulhan) Ф. 122
Прейер (Preyer) В 304, 305,
Рестиф 339
Рибо (Ribot) T. A. Ill, 200
Рид (Rent) T. 212
Рише Ш. 309
Робертсон (Roberbon) К. 217
Рубинштейн С. Л. 9
Розенталь 26
Романее, Ромэнс (Romanes)
Дж 221, 267, 268, 311
Руссо (Rousseau) Ж -Ж. 54,
339
Рэскин, Рсскин (Ruskin) Дж.
243
Саутгард (^outhgard) 320
Скотт 211
Скотт (Scott) В. 193
Скриб (Scribe) Э. 206
Смит (Smith) A. 143
Сократ (Sokrates) 144
Спалдинг (Spalding) 69, 299—
301
Спенсер (Spencer) Г. 20, 194,
286, 287, 289
Теккерей- (Thackeray) У. M.
Теннисон (lenn^son) A. 159
Титченер (Titchener) Э. Б. 5
Томсон (Thomson) P. б
Тэн (Taine) И. 79, 112
s'htctoh (Wheatstone) Ч. 218,
Уорьер (Wariier) 255
Учбанчич 39
Фере Ш (К.) 211
Фе\нер (Fechner) Г. Т. 31,
35-37, 100, 132
Фолькман А. В 185
Франц 208, 235
Холл (Hall) 126
Цезарь (Caesar) 123
Цшен Т. 39
Шарко (Charcot) Ж. M. 208
Шекспир (Shakespeare) У. 166
Шмидт Т. 211
Шнейдер (Schneider) К. 48,
271, 291, 309
Шопенгауэр (Shopenhauer) A.
Штейнталь (Steinthal) X 226
Штриккер 206, 207
Штрюмпелль (Striimpell) A.
Экснер 3. 181
Элиот (Eliot) Дж. 162
Эпиктет (Epictetus) 93
Юм (Hume) Д. 67, 70, 146
Ярошевский М. Г. 8
Предмегный указатель
Апперцепция 183, 22д—2;о, 227
Ассоциациг ii4—180 (гл XVI)
— основной закон 157, 158
— по смежности 190, 242, 250,
267
— по сходству 169—171, 177, 178,
264—267
— явления 155—157, 159. 166—
168, 17»
Вебера закон 31—35
Внимание 119—140 (гл XIII)
— виды 123—! 29
— и ассоциация 179, 180
— я воля 134, 140
— и гениальность 129—131
— избирательность 132, 133
— непроизвольное 123—126
— произвольное 123, 126—129
— рассеяние 120, 121
— физиологические условия 131-е
134
Воля 313—357 (гл XXVI)
— волевое усилие в внимание
139, 140, 310—342, 347—349,
357
—- определение 313, 314. 346, 347,
362
— патология 333—340
— «свобода воли»,152—355
Воображение 201—211 (гл. XIX»
— определение 201, 202
~ продуктивное и репродуктив-
ное 201, 202
— физиологическая основа 209—
Восприятие 180—187 (гл. XVII).
211—234 (гл. XX), 234—250 (гл.
XXI)
— времени 180—187
а) чувс1венное содержание
процесса восприятия времени
182, 183
б) возрастные особенности
восприягия времени 184
в) оценка длительнос1й вре-
мени 183—186
— как состояние сознания 213—
215
— определение 21)—213
— протяженности 234—236. 249,
250
— пространс1ва 234—250 (гл.
XXI)
— расстояния 243. 246—248
— физиологическая основа 215.
21Ь, 228, 229
Воспроизведение 165—168. 203—208
— двигательное 206, 207
— звуковое, звуковые образы
205—207
—— зрительное, сила зрительного
воспроизведения 203—205
— осязательное 207, 208
— факторы, определяющие его
характер 165—168
Галлюцинации 229—231, 233, 234
— сравнение о иллюзиями 231,
232
Гипноз
— и память 200. 201
Детерминизм (в психологии) 19,20
Диссоциации закон 153
Забывание 174. 175. 199, 200, 208,
209
Идеомочорное действие, 321—326
Иллюзии 216—225
Интереса закон lb3, 164
Инстинкт 289-313 (гл. XXV)
— изменчивости ингтинкгов за-
кон 300—304
—определение 289, 291, 295
— сравнение с опытом 29Э, 294
— сравнение с рефлексом 290
'— человеческие инстинкты, опи-
чие от животных 296, 297,
304—306
Контраста эффекты 40, 41
Концепт 140—145 (гл. XIV)
— объект 142, 143, 226 227, 255—
247, 328
— состояние сложной концепции
141
Личность 80—119 (гл. XII)
— духовная 85, 86, 90
•— иерархия 94—99
—— определение 81, 82
•— патологии, раздвоение лично-
сти 109—118
— самошждествеаность и созна-
ние 106—109
— социальная 83—85 88 89,
96—98
~ физическая 82. 83, 88
Метафизика 357, 388
Мнемонические приемы 198, 199
Мышление 250—269 (гл. XXII)
— непроизвольное течени(- мыс-
лей 159—163, 172
'— произвольное течение мыслей
172—177, 180
— процесс 2.U—253, 257—261
—— сравнение с ачоци.щиьй по
сходству 264— 'ДЛ
Относительности закон 38—40
Ощущения 24—41 цл. 11;, 234—
236, 238, 239, 244, 24а
— HHieHcriBHOCTh 31
— предметность 2а—31
—сравнение с воспришием 27—
29, 211-21d, 215
— физиологическая основа л, ^з
Память 187-201 (гл. XV 111)
— определение 187—1ва
~ па голо ги и 208, 209
— развитие 194, 195, lb6—198
— физиологическая схема 191—
— элементы, запоминание и при-
поминание 189-191, 19Ь, 197
Привычка 41—56 (гл. X)
— задерживающего влияния при-
вычек закон 297—300
— пракгнческое значение 44—46
— роль в воспитании 48—56
— физиологическая основа 41—44
Произвольные движения 315—321,
32fi, 350, 351
— сравнение с ингер^сом 345,
34Ь ^е
— условия возникновения о16,
316, 321
Построение реального пространства
236-246, 248, 249
Психические оберюны 71, 72, 327
Психология
— определение 17
— предмет 17—23
—— применение в педагогической
правке 48-56, 125, 138, 139,
194—106, 198, 228, ЛОЗ. 304
— сравнение о йсч-сгвенными
науками 17—19
— сравнение с философией 357—
Различение 145—154 (гл. XV).
262—2ЬЗ
—• и упражнения 153—154
— условия, благоприртстэуювдие
различению 147
Реинтегрлция 160—165
— неполная 163—165
— полная 160—164
Решимость и ее типы 327—332
Самонаблюдение 150, 151, 181, 182,
185, 213, 214, 240 278. 317. 318
Самооценка 86—88
Самоуважение 91—93
Сознание 56—80 (гл. XI), 100—104,
119—123. 182—189 213. 269,
361—363
— избирательная деятельность
75—80
—— и виды движений 269—272
— изменчивость состояний 65—68,
362, 3B:i
— ограниченность 119, 120
— объем 121—123
— поток 56—80
—- свойства 58—65. 182, 239
— сосюяния 17, 57. 65—71. 100—
104 '18, U9 189, 213, 269, 332,
361. 362
—г условия, определяющие со-
стояния 21, 22
— устойчивые состояния 65
Специфических энергий закон 26,
27
Страхи 2S4—286, 306—313
Умственные способности животных
267—269
Уровень притязаний 91—93
Фехнера закон 35—38
— критика 37, 38
— определение 35—37
Эмоции 272-289 (гл. XXIV)
— виды 273, 274, 283—285
" — объект 273
.— определение 274, 279, 280
— причины разнообразия 274, 280
— происхождение 275, 285—289
— сравнение с инстинктами 272.
273
'— теория основные положения
275—285
Эмпирическое «я» 81, 107—109
ОГЛАВЛЕНИЕ
К столетию «Принципов психологии» У Джемса 5
Предисловие автора ........... 14
Глава 1. Введение............ 17
Глава V1. Об ощущении вообще....... 24
Глава Х. Привычка........... 41
Глава XI. Поток сознания......... 56
Глава XII. Личность........... 80
Глава XIII. Внимание.......... 119
Глава XIV. Образование концептов..... 140
Глава XV. Различение.......... 145
Глава XVI. Ассоциация.......... 154
Глава XVII. Чувство времени....... 180
Глава XV1I1. Память........... 187
Глава XIX. Воображение......... 201
Глава XX Восприятие.......... 211
Глава XXI. Восприятие пространства..... 234
Глава XXII. Мышление...... 250
Глава XXIII, Сознание и движение..... 269
Глава XXIV. Эмоции.......... 272
Глава XXV. Инстинкт.......... 289
Глава XXVI. Воля............ 313
Эпилог. Психология и философия...... 356
Именной указатель........... 365
Предметвый указатель.......... 366
Методические указания по
выполнению контрольных работ
для студентов направления 010500 (510200) «Прикладная математика и информатика»
Санкт-Петербург
2009г.
Одобрено на заседании кафедры «Прикладная математика и эконометрика»
протокол № __ от __.__.2009г.
Утверждены Методическим советом ИЭУПС
протокол № __ от __.__.2009 г.
Методические указания написаны в объеме курса «Дискретная математика». Указания не включают в себя весь курс лекций по этой дисциплине, они содержат некоторые алгоритмы дисциплины, которые необходимо знать при выполнении индивидуальных заданий по данной дисциплине. Некоторые алгоритмы, имеющиеся в литературе, в указаниях представлены более доступно и на более простых примерах. При изучении материалов курса «Дискретная математика» необходимо наряду с методическими указаниями пользоваться литературой, перечисленной в библиографическом списке.
Цель данного курса – изложить методы работы с логическими элементами, а так же формирование знаний и умений, которые образуют теоретический фундамент, необходимый для постановки и реализации решения проблем в области прикладной математике.
Методические указания помогают в анализе дискретных структур возникающих как в пределах самой математике, так и в ее приложениях.
Методические указания составлены в соответствии с Государственным стандартом общего и профессионального образования. При подготовке методических указаний использовались последние публикации по теме «Дискретная математика» и материалы интернет ресурсов, в соответствии с этим был также составлен список рекомендуемой литературы.
Для успешного выполнения контрольной работы студент должен изучить соответствующий теоретический материал и ознакомиться с решением типовых примеров, приведенных в настоящих указаниях. Контрольные работы составлены по трем темам: «Дискретные множества» и «Элементы математической логики» и «Элементы теории графов».
Составители: О.Х. Бритаева, ст.преподаватель
Рецензент: проф. каф. ПМиЭ СПбГУСЭ д.ф.-м.н. Шерстюк А.И.
СОДЕРЖАНИЕ
| Предисловие | |
| Глава I.Дискретные множества | |
| ГлаваII.Элементы математической логики | |
| Глава III.Элементы теории графов | |
| Глава IV.Задания для самостоятельной работы | |
| Рекомендуемаялитература |
Предисловие
Основное отличие дискретной математики от классической заключается в отсутствии понятия бесконечности, предела и непрерывности, а основными носителями являются: целые числа, многочлены, матрицы, слова и т.п., которые находятся между собой в каких-то отношениях. Эти отношения могут изменяться в дискретные моменты времени.
При организации каких-либо экономических или производственных процессов, при передаче управленческих решений важным условием является дискретность при обработке информации. Состав и структура дискретных систем представляют дискретные модели для описания которой привлекается аппарат дискретной математике.
Изучение учебной дисциплины «Дискретная математика» базируется на знаниях, полученных в результате освоения дисциплин «Высшая математика» и «Информатика» Изучение курса позволяет:
– ознакомиться с основами таких направлений дискретной математики, как теория множеств, теория графов и теория булевых функций;
–получить представление о теоретических основах и методах дискретной математики для описания и исследования объектов реального мира и построения математических моделей.
В результате изучения дисциплины студенты должны:
– получить представление о понятиях и теоретических моделях изучаемых направлений дискретной математики;
– освоить приемы применения теоретических моделей для описания предлагаемых заданий и получения результатов;
– приобрести практические навыки по отработке формализованных описаний объектов методами дискретной математики.
Предлагаемые методические указания состоят из трёх разделов:
- дискретные множества
- элементы математической логики
- элементы теории графов
За основу методических указаний принят материал курса, читаемого в СПбГУСЭ бакалаврам специальности 010500.62 (510200) «Прикладная математика и информатика».
Студенты остальных специальностей могут использовать методические указания как вспомогательный материал.
Формой контроля усвоения дисциплины учебным планом предусмотрены зачеты. В течение двух семестров выполняются письменные контрольные работы (семинарские и домашние индивидуальные задания). Выполнение контрольных работ является обязательным для всех студентов, а результаты текущего контроля служат основанием для выставления аттестации в ведомость промежуточного контроля. Индивидуальные задания составлены так, что если студент выполняет их самостоятельно, то подготовка его к зачету займет незначительное время. При возникновении затруднений при решении задач студент может обратиться (устно или письменно) за консультацией на кафедру «Прикладная математика и эконометрика» СПбГУСЭ.
Предлагаемые методические указания состоят из трех разделов, взаимосвязь между которыми прослеживается при рассмотрении различных иллюстрирующих примеров.
Первый раздел методических указанийпосвящен решению дискретных задач, с помощью теории множеств и математической логики.
Второй раздел посвящен основным понятиям математической логики, т.е. анализу задач методом рассуждений. Исследуются соотношения между основными понятиями математики на базе которых доказываются математические утверждения.
Третий раздел посвящен теории графов, особенностью которой является геометрический подход к изучению объектов. Теория графов находит применение в программировании, в теории конечных автоматов, в решении вероятностных и комбинаторных задач.
Все разделы имеют сходную структуру. Вначале даются необходимые определения, способы описания рассматриваемого объекта, затем вводится операция позволяющая получать одни объекты из других. Изложение материала сопровождается задачами, решением которых рекомендуется для лучшего понимания материала.
ГЛАВА 1. «ДИСКРЕТНЫЕ МНОЖЕСТВА»
Множество это любое собрание определенных и различимых между собой объектов нашей интуиции или интеллекта, мыслимое как единое целое. Эти объекты называются элементами или членами множества. Множества обозначаются прописными латинскими буквами (А, В, С,…) а их элементы – строчными (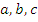 ,…). Множества могут быть конечными (группа студентов) или бесконечными (натуральные числа). Множества, элементами которых являются тоже множества называют классом (семейством, системой) множеств.
,…). Множества могут быть конечными (группа студентов) или бесконечными (натуральные числа). Множества, элементами которых являются тоже множества называют классом (семейством, системой) множеств.
Для конечного множества  количество элементов n – называется мощностью множества и обозначается
количество элементов n – называется мощностью множества и обозначается  . По конкретному элементу а и множеству А можно определить принадлежит элемент а множеству А
. По конкретному элементу а и множеству А можно определить принадлежит элемент а множеству А  или не принадлежит
или не принадлежит  .
.
Множество, состоящее из одного элемента, обозначается  . Множество, не содержащее элементов, называется пустым и обозначается
. Множество, не содержащее элементов, называется пустым и обозначается 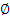 (например,
(например,  ).
).
Операции над множествами позволяют получить новые множества.
Вложенность множеств (подмножество, надмножество): операция  . Пусть
. Пусть 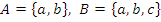 , тогда
, тогда  (A есть подмножество В, т.е. А вложено, содержит в В; В есть надмножество над А, т.е. В содержит А).
(A есть подмножество В, т.е. А вложено, содержит в В; В есть надмножество над А, т.е. В содержит А).
Объединение множеств: операции  . Пусть
. Пусть  , тогда
, тогда 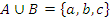 (все элементы множеств А и В без повторения элементов).
(все элементы множеств А и В без повторения элементов).
Пересечение множеств: операция 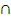 . Пусть
. Пусть  , тогда
, тогда  (элементы общие для множеств А и В).
(элементы общие для множеств А и В).
Дополнение множеств: операция \ (разность). Пусть  , тогда
, тогда 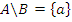 (все элементы множества А, не принадлежащие В, т.е. из А вычитаются элементы, общие с В).
(все элементы множества А, не принадлежащие В, т.е. из А вычитаются элементы, общие с В).
Симметрическая разность: операция –. Пусть 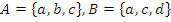 , тогда
, тогда 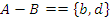 (все элементы А, не принадлежащие В, и все элементы В, не принадлежащие А).
(все элементы А, не принадлежащие В, и все элементы В, не принадлежащие А).
Равенства множеств: операция =.  справедливо тогда и только тогда, когда
справедливо тогда и только тогда, когда  и
и 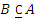 .
.
Справедливы отношения: 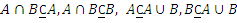 .
.
Например, если  , то
, то  , поэтому из приведенных выше соотношений следует, сто
, поэтому из приведенных выше соотношений следует, сто 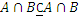 . Справедливы также формулы дистрибутивности:
. Справедливы также формулы дистрибутивности:  .
.
Диаграммами Эйлера-Венна называют фигуры, изображающие на плоскости множества и наглядно демонстрирующие свойства операций над ними.
Пусть квадрат Е на плоскости обозначает некоторое универсальное множество, которое включает в себя все рассматриваемые множества.
| Заштриховано дополнение множества A | 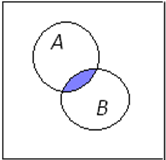
| Заштриховано пересечение 
| |||
| Заштриховано объединение 
| 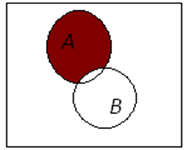
| Заштрихована разность 
| |||
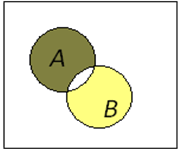
| Заштрихована симметрическая разность |
Булеаном называется множество всех подмножеств множества М и обозначается В(М), а множество М называется универсумом, или универсальным. Каждое множество  имеет, по крайней мере, два различных элемента: само М и
имеет, по крайней мере, два различных элемента: само М и 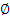 . Пусть
. Пусть 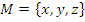 , тогда его булеан
, тогда его булеан 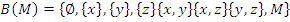 . Мощность булеана от универсума
. Мощность булеана от универсума 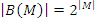 . Например
. Например 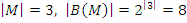 .
.
Алгебра множеств определяет правила выполнения операций над множествами. Множество М вместе с заданной на нем совокупностью операций 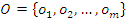 , т.е. система
, т.е. система  называется алгеброй; М называется основным множеством (носителем) алгебры А.
называется алгеброй; М называется основным множеством (носителем) алгебры А.
Пусть задано универсальное множество U; его булеан B(U). Совокупность операций 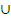 (объединения),
(объединения), 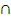 (пересечения),
(пересечения),  (дополнения, отрицания) называются булевыми операциями. Алгебра
(дополнения, отрицания) называются булевыми операциями. Алгебра 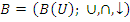 называется булевой алгеброй множеств над U. Элементами основного множества этой алгебры являются подмножества А, В, С, … множества U. Операция
называется булевой алгеброй множеств над U. Элементами основного множества этой алгебры являются подмножества А, В, С, … множества U. Операция 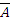 эквивалентна операции дополнения
эквивалентна операции дополнения  . Для универсума U и его подмножеств при использовании булевых операций выполняются следующие свойства (тождества алгебры множеств):
. Для универсума U и его подмножеств при использовании булевых операций выполняются следующие свойства (тождества алгебры множеств):
| Идемпотентность (удаление одинаковых операндов): | |
а) 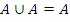 ; ;
| б)  . .
|
| Коммутативность (перестановка операндов): | |
а) 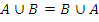 ; ;
| б)  . .
|
| Ассоциативность (возможность бесскобочной записи): | |
а) 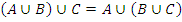 ; ;
| б) 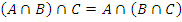
|
| Дистрибутивность (раскрытие скобок): | |
а) 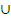 относительно относительно 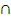
| б) 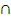 относительно относительно 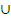
|
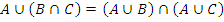 ; ;
|  . .
|
| Поглощение: | |
а) 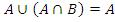 ; ;
| б) 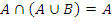 . .
|
| Законы (правила) де Моргана: | |
а)  ; ;
| б) 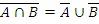 . .
|
| Обобщение правила де Моргана для совокупности множеств: | |
а) 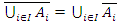 ; ;
| б) 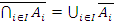 . .
|
| Свойства универсума: | |
а)  ; ;
| б)  . .
|
| Свойства пустого множества: | |
а)  ; ;
| б)  . .
|
| Свойства дополнения (отрицания): | |
а)  ; ;
| б)  . .
|
| Свойства двойного дополнения (отрицания): | |
 . .
|
Пары свойств двойственны друг другу в том смысле, что если в одном из них заменить 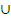 на
на 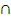 ,
,  на
на 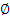 , и наоборот, то получим парное свойство.
, и наоборот, то получим парное свойство.
С целью упрощения формул предполагается, что знак дополнения (отрицания) играет роль скобок, а при отсутствии скобок порядок выполнения операций следующий: дополнение, пересечение, объединение.
Формулы алгебры множеств. Выражение, компонентами которого являются элементы носителя алгебры множеств и символы алгебраических операций, называют формулой F.
Множества A,B,C,… называют элементарными формулами.
Выражения  называют формулами первого порядка, а
называют формулами первого порядка, а  ,
,  – второго и более высоких порядков.
– второго и более высоких порядков.
Никаких иных формул в алгебре множеств нет.
Эквивалентные преобразования формул. Опираясь на законы алгебры множеств, можно выполнять эквивалентные преобразования формул, упрощая их описания. При преобразовании алгебраических выражений необходимо прежде всего устранить операторы разности – “\”и симметрической разности “∆”, т.е. использовать только основную сигнатуру алгебру множеств – 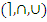 .
.
При написании сложного алгебраического выражения следует помнить, что:
 относится к непосредственно следующей формуле
относится к непосредственно следующей формуле  ;
;
 следует прежде всего опустить от формулы n -го порядка к элементарной формуле по
следует прежде всего опустить от формулы n -го порядка к элементарной формуле по 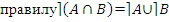
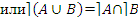 ;
;
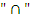 относится к непосредственно окружающим формулам;
относится к непосредственно окружающим формулам;
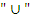 относится к непосредственно окружающим формулам;
относится к непосредственно окружающим формулам;
Операция 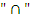 сильнее
сильнее 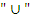 , что позволяет опускать скобки “(“ и “)”, например,
, что позволяет опускать скобки “(“ и “)”, например,  .
.
Пример: Пусть 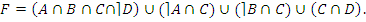
· по закону коммутативности:
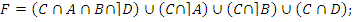
· по закону дистрибутивности:
 ;
;
· по закону дистрибутивности:
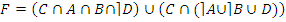 ;
;
· по закону дистрибутивности:
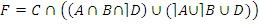 ;
;
· по закону де Моргана:
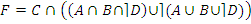 ;ж
;ж
· по закону «третьего не дано»:

· по закону универсального множества: F=C
Таким образом 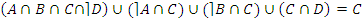 .
.
Пример: Пусть  .
.
· замена разности множеств:
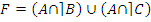 .
.
· по закону дистрибутивности:
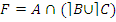 ;
;
· по закону де Моргана:
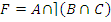 ;
;
· замена пересечения с дополнением на разность множеств:
 .
.
Таким образом 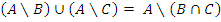 .
.
Пример: Пусть  .
.
· Замена симметрической разности:
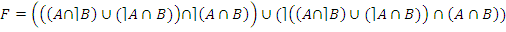 ;
;
· по закону де Моргана:
 ;
;
· по закону де Моргана:
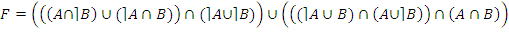 ;
;
· по закону дистрибутивности:
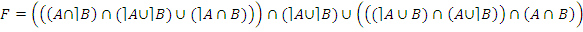 ;
;
· по закону дистрибутивности:
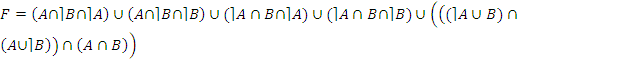 ;
;
· по законам идемпотентности и противоречия:
 ;
;
· по закону дистрибутивности:
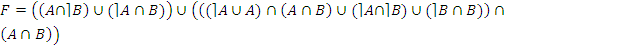 ;
;
· по закону противоречия:
 ;
;
· по закону дистрибутивности:
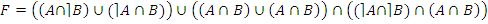 ;
;
· по законам идемпотентности и противоречия:
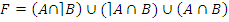 ;
;
· по закону дистрибутивности:
 ;
;
· по закону «третьего не дано»:
 .
.
Таким образом 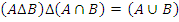 .
.
Пример: Изобразим с помощью диаграммы Эйлера-Венна множество 
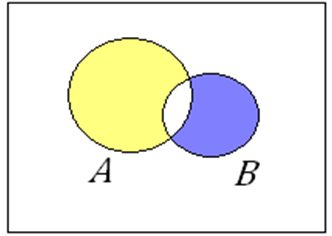
Это множество является объединением двух разностей, называется симметрической разностью и обозначается  , Т.Е.
, Т.Е.  .
.
ГЛАВА 2. «ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ»
Математическая логика – современный вид формальной логики, т.е. наука, изучающая умозаключения с точки зрения их формального строения. Выделяется несколько типов формальных систем: логика высказываний и логика предикатов, логика отношений и нечеткая логика и др.
Логика высказываний – это простейшая из формальных логических теорий.
Высказывания – повествовательные предложения, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно. Высказывания бывают простые и составные.
В логике высказываний истинное значение обозначается 1, а ложное 0.
Высказывания обозначаются прописными буквами латинского алфавита: X, Y, Z ….
Составные высказывания получаются из простых с помощью логических операций: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность, которые осуществляются при помощи логических связок: 
| Название | Прочтение | Обозначение |
| Отрицание | не | 
|
| Конъюнкция | и | 
|
| Дизъюнкция | или | 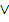
|
| Импликация | если…то | 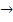
|
| Эквивалентность | тогда и только тогда, когда | 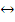
|
Таблица истинности – это интерпретация логических операций, в каждой строке таблице наборы из нолей и единиц соответствующие составляющим высказывания.
Пусть даны два произвольных высказывания X и Y.
Отрицанием высказывания X называется высказывание 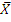 , которое истинно, когда X ложно, и ложно, когда X истинно.
, которое истинно, когда X ложно, и ложно, когда X истинно.
Таблица истинности для отрицания.
| X | 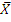
|
Конъюнкцией двух высказываний X и Y называется высказывание X  Y, которое истинно только в том случае, когда X и Y оба истинны.
Y, которое истинно только в том случае, когда X и Y оба истинны.
Таблица истинности для конъюнкций.
| X | Y | X  Y Y
|
Дизъюнкцией двух высказываний X и Y называется высказывание X 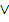 Y, которое истинно, когда хотя бы одно из них истинно.
Y, которое истинно, когда хотя бы одно из них истинно.
Таблица истинности дизъюнкций.
| X | Y | X 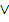 Y Y
|
Импликацией двух высказываний X и Y называется высказывание X 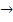 Y, которое ложно тогда и только тогда, когда X истинно, а Y ложно.
Y, которое ложно тогда и только тогда, когда X истинно, а Y ложно.
Таблица истинности для импликации.
| X | Y | X 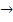 Y Y
|
Эквивалентностью высказываний X и Y называется высказывание  , которое истинно тогда и только тогда, когда X и Y оба истинны или ложны.
, которое истинно тогда и только тогда, когда X и Y оба истинны или ложны.
Таблица истинности для эквивалентности.
| X | Y | X 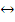 Y Y
|
Для образования составных высказываний используются многократные и единичные основные связки. Вначале читается выражение во внутренних скобках затем эти скобки в свою очередь группируются и т.д.. Если скобок нет то операции надо выполнять в следующем порядке: конъюнкция, дизъюнкция, импликация, эквивалентность, отрицание. Каждое составное высказывание имеет свою таблицу истинности, которая может быть построена стандартным образом.
Новые высказывания могут быть образованы при помощи нескольких логических операций и могут составлять формулы, некоторые из которых рассматриваются как логические операции, осуществляемые при помощи других логических связок:│; ↓;  .
.
| Название | Прочтение | Обозначение |
| Штрих Шеффера | Антиконъюнкция | | |
| Стрелка Пирса | Антидизъюнкция | ↓ |
| Сумма по модулю два | Антиэквивалентность | 
|
Штрих Шеффера, X | Y или антиконъюнкция, по определению (X | Y) =  .
.
Таблица истинности штриха Шеффера.
| X | Y | X\Y |
Стрелка Пирса, или антидизъюнкция, по определению X ↓ У = = 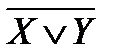 .
.
Таблица истинности стрелки Пирса.
| X | У | X ↓ Y |
Сумма по модулю два, или антиэквивалентность, по определению 
Таблица истинности суммы по модулю два.
| X | У | 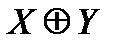
|
Таблицы истинности логических операций содержат 2n строк, где п — число простых высказываний.
В случаях составных высказываний, имеющих одни и те же компоненты, по таблицам истинности, можно проверить, имеет ли место отношение следствия.
Например:
| X | У | X ↔Y | Х→У | XVY |
ВысказываниеX ↔Y истинно в первом и четвертом случаях и в обоих этих случаях истинно также высказывание X → Y. Мы видим, что из X ↔ Y следует высказывание
X → Y. Сравнение двух последних столбцов показывает, что из высказывания X → Y не следует X V Y, из X V У не следует X → Y.
При помощи таблиц истинности удобно осуществлять проверку эквивалентности двух составных высказываний, имеющих одни и те же компоненты. Для этого достаточно лишь посмотреть, одинаковы ли таблицы истинности у этих составных высказываний.
Из следующей таблицы истинности видно, что X → У эквивалентно 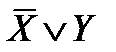 .
.
| X | У | X → У | 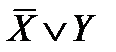
|
Два высказывания называются логически несовместимыми, если из истинности одного из них необходимо следует ложность другого. Другими словами, несовместимость высказываний X и У означает, что они никогда не могут оказаться одновременно истинными. Если несколько составных высказываний построены из одних и тех же простых составляющих, то для проверки их совместимости нужно построить таблицы истинности для каждого из высказываний. Если среди всех строк найдется, по крайней мере, одна, в которой все составные высказывания истинны, то составные высказывания совместимы. В противном случае они оказываются несовместимыми.
Импликация двух высказываний отличается от эквивалентности, а также от дизъюнкции и конъюнкции тем, что она несимметрична. Так X V У эквивалентно У V X;
 эквивалентно
эквивалентно 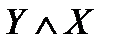 ; X ↔ У эквивалентно У ↔ X, но X → У не эквивалентно
; X ↔ У эквивалентно У ↔ X, но X → У не эквивалентно
У → X. Высказывание У → X называется конверсией высказывания X → У.
В таблице истинности представлены четыре импликации и их названия.
| X | У | 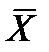
| 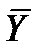
| Импликация Х→У | Конверсия импликации У → X | Конверсия контрапозиции
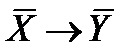
| Контрапозиция 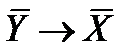
|
Из таблицы видно, что X → У эквивалентно 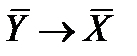 . Последнее называется контрапозицией первого. Контрапозиция является удобной формой импликации во многих рассуждениях. Аналогично, высказывание
. Последнее называется контрапозицией первого. Контрапозиция является удобной формой импликации во многих рассуждениях. Аналогично, высказывание  представляет собой конверсию контрапозиции. Так как контрапозиция эквивалентна
представляет собой конверсию контрапозиции. Так как контрапозиция эквивалентна  , то конверсия этой контрапозиции эквивалентна конверсии этой импликации.
, то конверсия этой контрапозиции эквивалентна конверсии этой импликации.
С импликацией связано постоянное упоминание математиками «необходимое условие» и «достаточное условие».
| X является достаточным условием для У | Если имеет место X, то У также будет иметь место | Импликация X →У |
| X является необходимым условием для У | Если имеет место У, то X также будет иметь место | Конверсия достаточного условия У →X |
| X является необходимым и достаточным условием для У | X имеет место, если и только если имеет место У | Двойная импликация X↔У эквивалентность |
.
|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 1146; Нарушение авторских прав?; Мы поможем в написании вашей работы!
