Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы

Любая булева функция может иметь много представлений в виде ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).

Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, в которой в каждый конъюнктивный одночлен каждая переменная х_i из набора f(x₁, x₂,..., х_п) входит ровно один раз, причем входит либо сама х_i, либо ее отрицание .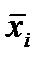

Конструктивно СДНФ для каждой формулы алгебры высказываний, приведенной к ДНФ, молено определить так:

Совершенной дизъюнктивной нормальной формой (СДНФ) формулы алгебры высказываний называется ее ДНФ, обладающая следующими свойствами:

1. ДНФ не содержит двух одинаковых конъюнкций.

2. Ни одна конъюнкция не содержит одновременно двух одинаковых переменных.

3. Ни одна конъюнкция не содержит одновременно некоторую переменную и ее отрицание.

4. Каждая конъюнкция содержит либо переменную Х\, либо ее отри­цание х7 для всех переменных, входящих в формулу.

Конструктивно СКНФ для каждой формулы алгебры высказываний, приведенной к КНФ, можно определить так:

Совершенной конъюнктивной нормальной формой (СКНФ) данной формулы алгебры высказываний называется такая ее КНФ, которая удовлетворяет следующим свойствам:

1. КНФ не содержит двух одинаковых дизъюнкций.

2. Ни одна из дизъюнкций не содержит одновременно двух одинако­вых переменных.

3. Ни одна из дизъюнкций не содержит одновременно некоторую пе­ременную и ее отрицание.

4. Каждая дизъюнкция СКНФ содержит либо переменную х_i либо ее отрицание х_i для всех переменных, входящих в формулу.

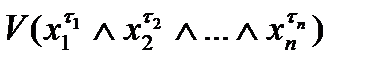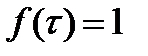Теорема 1 Произвольную булеву функцию f(xi,x₂,...,х_п) можно задать формулой f(x₁,x₂,...,х_п) = , где дизъюнкция берется по всем , где и

.

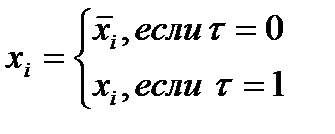Теорема 2. Произвольную булеву функцию f(xi, x₂,...,х_п) можно задать формулой f(xi,x₂, …,х_п) = 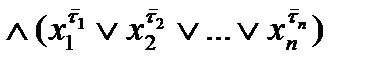где конъюнкция берется по всем 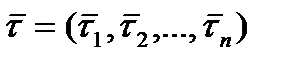, где и

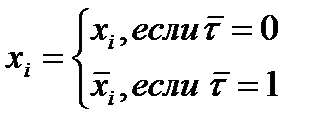
Эти формулы называются соответственно совершенной дизъюнктивной нормальной формой или совершенной конъюнктивной нормальной формой булевой функции f(x₁,x₂,...,х_п). Исходя из таблицы истинно­сти булевой функции, можно построить СДНФ функции: для каждого набора , такого, что 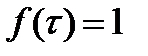, составляется конъюнкция 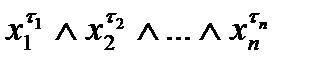, а затем все эти конъюнкции соединяем знаком дизъ­юнкции.

Для построения СКНФ функции выписываем наборы 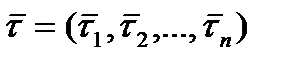такие, что . Для такого набора составляется дизъюнкция 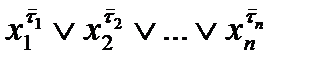, а затем все такие дизъюнкции соединяют знаком конъюнкции.

Приведенные формулы позволяют сформулировать следующие утверждения:

1. Каждая булева функция от п переменных, отличная от константы 0, имеет единственную СДНФ.

2. Каждая булева функция от п переменных, отличная от константы 1, имеет единственную СКНФ.

Эти утверждения называются теоремой о функциональной полноте.

Дата добавления: 2014-11-07