Свойства элементарных булевых функций

Для булевых функций справедливы равенства, аналогичные формулам, сформулированным для высказываний.

1. Функции: конъюнкция, дизъюнкция, сумма по модулю два, стрелка Пирса, штрих Шеффера обладают свойством коммутативности.

2. Функции: конъюнкция, дизъюнкция, сумма по модулю два обладают свойством ассоциативности и свойством дистрибутивности.

3. Закон де Моргана:

4. Закон двойного отрицания: 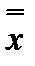= х.

5. Выражение дизъюнкции через конъюнкцию и суммы по модулю два: .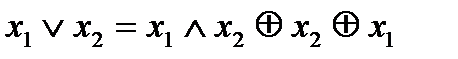

6. Выражение дизъюнкции через импликацию:

.

7. Выражение отрицания через штрих Шеффера, стрелку Пирса, сумму по модулю два и эквивалентность: .

8. Выражение конъюнкции через штрих Шеффера:

.

9. Выражение дизъюнкции через стрелку Пирса:

.

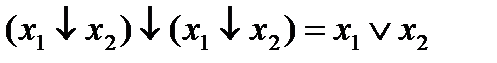10. Закон поглощения: .

11. Закон склеивания:.

12. Для функций: конъюнкция, дизъюнкция и сумма по модулю два справедливы следующие тождества:

; ; ;

; ; ;

;. ; ;

; ; .

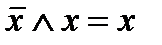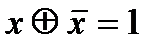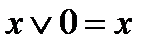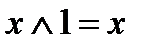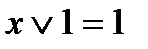13. Для функций конъюнкция и дизъюнкция справедливы тождества: Для доказательства справедливости любых из приведенных тождеств нужно составить таблицы истинности для булевых функций.

Булеву функцию любого числа переменных можно задать формулой, содержащей функции одной и двух переменных посредством подстановки одних булевых функций вместо переменных в другие булевы функции, т. е. посредством суперпозиции булевых функций.

Дата добавления: 2014-11-07