Многочлены Жегалкина

Любую булеву функцию можно представить в виде многочлена от своих переменных и такой многочлен называется многочленом Жегалкина.

Многочленом Жегалкина называется многочлен, являющийся суммой константы и различных одночленов, в которые каждая из переменных входит не выше, чем в первой степени.

Многочлен Жегалкина константы равен самой же константе; мно­гочлен Жегалкина булевой функции одной переменной f(x) = многочлен Жегалкина булевой функции двух переменных

f(x₁,x₂) = ;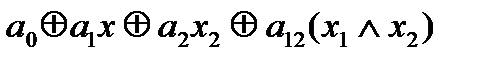

многочлен Жегалкина булевой функции трех переменных

f(x₁,x₂,x₃)= 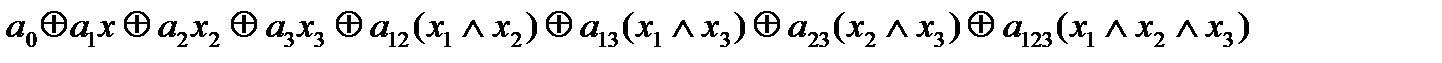и т.д. Коэффициенты a₁,...,_i и свободный член а_о принимают значения О или 1, а число слагаемых в формуле равно 2^п, где п — число переменных. Знак — сумма Жегалкина или сумма по модулю два.

Теорема	3 (Жегалкина).	Каждая булева функция	f(x1,x2,...,хп)	может
быть представлена в виде	многочлена Жегалкина и	единственным
образом,	с точностью до порядка слагаемых.

Сформулируем алгоритм построения многочлена Жегалкина. Выше было указано, что любую функцию, отличную от константы О, можно представить в виде СДНФ. Если сравним таблицы истинности

дизъюнкции и суммы по модулю два, видим, что они отличаются только последней строкой, т. е. на наборе 11. Так как в СДНФ на каждом наборе только одна конъюнкция равна 1, то все дизъюнкции можно заменить суммами по модулю два. Кроме того, известно, что . На этом и основан первый алгоритм построения многочлена Жегалкина:

1. Находим множество тех двоичных наборов, на которых функция принимает значение 1.

2. Составляем СДНФ.

3. В СДНФ каждый знак дизъюнкции меняем на знак суммы Жегалкина.

4. Упрощаем, если можно, полученное выражение, используя тождество .

5. В полученной формуле каждое отрицание заменяем на .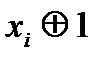

6. Раскрываем скобки в полученной формуле, содержащей только
функции и и константу 1.

7. Приводим подобные члены, используя тождество .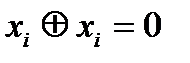
Используя метод неопределенных коэффициентов, получаем второй алгоритм определения многочлена Жегалкина:

1. Составляем систему линейных уравнений относительно 2^п неизвестных коэффициентов, содержащую 2^п уравнений, решением которой являются коэффициенты а_о, а₁, …,а_1,2…n многочлена Жегалкина.

Многочлен Жегалкина называется нелинейным, если он содержит конъюнкции переменных, а если он не содержит конъюнкции перемен­ных, то он называется линейным.

Функция f(x₁,х₂,...,х_п) называется линейной, если ее многочлен Жегалкина имеет вид и нелинейной в противном случае.

Из определения многочлена Жегалкина следует, что для любой буле­вой функции коэффициенты при переменных x₁,х₂,...,х_п и свободный член вычисляются по формулам:

,

,

…

.

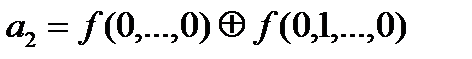На этом основан алгоритм определения линейности (или нелинейности) булевой функции.

1. По таблицам истинности булевой функции f(x₁,х₂,...,х_п) и выше указанным формулам находим коэффициенты: (а_о, а₁, …,а_1,…n)

2. Выписываем многочлен Ф(x₁,...,х_п)= и проверяем, задает ли он эту функцию. Для этого строим таблицу истинности многочлена Ф(x₁,х₂,...,х_п) и сравниваем ее с таблицей истинности функции f(x₁,x₂,...,х_п).

Задача. Задана булева функция трех переменных:

;

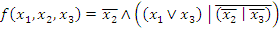а) постройте таблицу истинности, найдите двоичную форму F булевой функции и приведите функцию к СДНФ и СКНФ,

б) найдите двумя способами многочлен Жегалкина.

Решение.

а)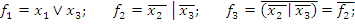

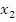
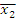
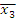
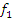
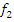
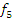
Двоичная форма F= 11000100

Наборы =(000, 001, 101), где .

СДНФ функции .

Наборы =(010, 011, 100, 110, 111), где .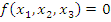

СКНФ функции

б) Построим многочлен Жегалкина первым способом:

выписываем СДНФ функции

;

заменяем знак дизъюнкции на знак суммы Жегалкина

,

вынесем из первой и второй конъюнкции :

;

проделаем замены: , получим:

.

Далее раскроем скобки:

.

Итак, мы получим многочлен Жегалкина:

.

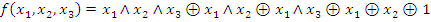Построим многочлен Жегалкина методом неопределенных коэффициентов, для этого составим следующие восемь уравнений:

;

;

;

;

;

;

;

;

.

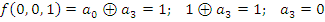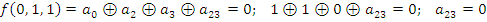Составим многочлен Жегалкина:

.

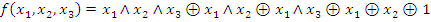Задача. Задана булева функция трех переменных

.

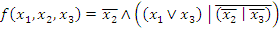С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ.

Решение. Заменяем, ,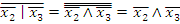

.

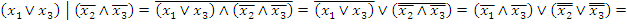
, тогда

ДНФ ,

КНФ .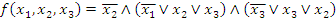

Строим СДНФ, для этого из ДНФ удаляем вторую конъюнкцию 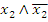, а в третью конъюнкцию добавляем , тогда:

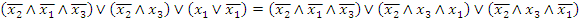, т.е. получили СДНФ функции

.

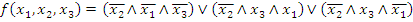Строим СКНФ, для этого из КНФ удаляем третью дизъюнкцию, а к первой добавляем :

,

добавляем к первой и второй дизъюнкциям

.

Получили СКНФ функции

.

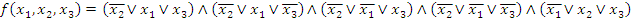ГЛАВА III. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ

Теория графов, являясь разделом дискретной математики, используется для описания и изучения отношений между дискретными объектами. При этом объекты геометрически можно представить в виде множества точек, называемых вершинами графа, некоторые из которых объявляются смежными (или соседними). Считается, что смежные вершины соединены между собой ребрами (или дугами). Обозначается G=(V,X).

Таким образом, ребро определяется парой вершин. Два ребра, у которых есть общая вершина, так же называется смежными (или соединенными). Ребро (дуга) и любая из его двух вершин называется инцидентными.

Граф называется ориентированным (или орграфом), если ребра имеют направление. Это означает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет.

Помимо этого, в теории графов рассматриваются также мультиграфы – это такие графы, в которых могут быть петли (т.е. некоторая вершина соединена сама с собой ребром) или некоторые пары вершины могут быть соединены между собой несколькими ребрами.

Пример 1. Задан граф G, состоящий из вершин v₁, v_2, v₃, v₄, v₅, v₆ и ребер x₁, x₂, x₃, x₄, x₅: x₁=(v₁, v₂), x₂=(v₁, v₄), x₃=(v₅, v₆), x₄=(v₁, v₂), x₅=(v₅, v₆). (см. рис. 1)

x₄

x₂

x₃

x₅

x₁

v₁

v₂

v₄

v₅

v₃

v₆

Рис. 1

x₁ и x₄ - кратные ребра, x₅ – петля,

x₁ и x₂ – смежные ребра, x₁ – инцидентно v₁ и v₂,

v₁ и v₄ – смежные вершины.

Маршрут в графе – это последовательность соседних (смежных) вершин. Ясно, что можно определить маршрут и как последовательность смежный ребер (в этом случае ребра приобретают направление). Заметим, что в маршруте могут повторяться вершины, на не ребра. Маршрут называется циклом, если в нем первая вершина совпадает с последней.

Путь в графе (иногда говорят простой путь) – это маршрут без повторения вершин (а значит, и ребер).

Контур – это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней.

Последовательности вершин (рис. 2): 1-2-3-4-2-5 не простой путь, а маршрут; последовательности 1-2-3-4-7-5 и 1-2-5 - простые пути; 1-2-3-4-2-5-6-1 – это цикл (но не контур); 1-2-5-6-1 – это контур.

Рис. 2

Если имеется некоторый маршрут из вершины t в вершину s, заданный в виде последовательности ребер, которые в этом случае приобрели направление, и если в этот маршрут входит ребро, соединяющее вершины (i,j),то это ребро по отношению к вершине i называют иногда прямой дугой, а по отношению к вершине j – обратной дугой (или обратным ребром).

Граф называется связанным, если любые две его вершины можно соединить маршрутом (или путем). На рис. 1 изображен связный граф.

Ребро, при удалении которого граф перестает быть связным, иногда называют мостом или перешейком.

Следующее определение имеет смысл только для графов или мультиграфов без петель (но не для орграфов).

Степень вершины (валентность) –это число ребер, входящих в эту вершину число инцидентных вершине ребер. Вершина называется висячей если ее степень равна единице. Обозначают d_i или deg v_i.

Петля добавляет 2 в степень вершины.

В примере 1: d₁=3, d₂=2, d₃=0, d₄=1, d₅=3, d₆=1, т.е. v₃ – изолированная вершина, v₄ и v₆ – висячие вершины.

(число ребер).

Сумма степень вершин графа G всегда равна 2m, где m – число ребер графа G/в любом графе число вершин с нечетными степенями четно.

Если степень всех вершин в графе больше или равна двум, то граф обязательно содержит контур.

Два графа G=(V, X) и H=(W, Y) называют изоморфными, если между их множествами вершин V и W существует взаимнооднозначное соответствие, сохраняющее смежность. Изоморфизм есть отношение эквивалентности на графах. Из определения следует, что изоморфные графы отличаются лишь обозначением вершин.

Пример 2. Графы G и H, изображенные на рис. 3, изоморфны.

Рис. 3

Для того, чтобы доказать их изоморфность достаточно пометить их вершины в соответствующем порядке (рис. 4):

Рис. 4

Инвариант графа G – это число, связанное с G, которое принимает одно и то же значение на любой графе, изоморфном G. Числа n (число вершин графа) и m (число ребер) являются инвариантами графа. Полный набор инвариантов определяет граф с точностью до изоморфизма. Например, числа n и m образуют полный набор инвариантов для всех графов с n<4.

Подграфом G=(V, X) графа G=(V, X) называется граф, у которого все вершины и ребра (дуги) принадлежат G: V, V, X X, каждое из ребер x_i инцидентно только вершинам из V. Если G – подграф G,то G – надграф (super-graf) графа G. Основной подграф – это подграф G, содержащий все его вершины.

Для компьютерной обработки используется матричная форма представления структурных свойств графа.

Это следующие матрицы:

1. Матрица смежности. Это квадратная матрица порядка n (n – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно p), то на главной диагонали в строчке с номером k стоит число p). Если вершина i связана с вершиной одним ребром, то элемент матрицы смежности a_ij равен 1, если эти вершины связаны s ребрами, то a_ij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов.

Матрица смежности A(G) определяет граф G с точностью до изоморфизма; она является симметричной матрицей с нулями по главной диагонали. Сумма элементов по строкам матрицы A(G) равна степеням вершин графа G.

v₂

v₁

v₅

v₄

v₃

G:

Пример 6.

Рис. 5

Так как у графа G 5 вершин, то размер матрицы A (G), будет 5х5:

a₁₂=1, т.к. в графе G есть ребро, соединяющее вершины v₁ и v₂; a₄₂=0, т.к. в графе G нет ребра, соединяющего вершины v₄ и v₂ и т.д.

Если A – матрица смежности графа G, то элемент матрицы Aⁿ , стоящий в i-той строке и j-том столбце, будет равен числу маршрутов длины n из вершины v_i и v_j.

Для примера 6 имеем:

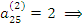существует 2 маршрута длины 2 из вершины v₂ в вершину v₅: v₂-v₁-v₅ и v₂-v₃-v₅;

существует 7 маршрутов длины 3 из вершины v₅ в вершину v₃: v₅-v₁-v₂-v₃, v₅-v₁-v₅-v₃, v₅-v₄-v₅-v₁, v₅-v₃-v₅-v₃, v₅-v₃-v₁-v₃, v₅-v₃-v₂-v₃, v₅-v₃-v₄-v₃.

Матрицей смежности орграфа D называется квадратная матрица A(D) порядка n (n- число) с вершинами элемента:

Матрица смежности орграфа в общем случае не будет симметричной.

Пример 7. Дан орграф D:

Рис. 6

Так как у графа D 6 вершин, то размер матрицы A(D) будет 6х6:

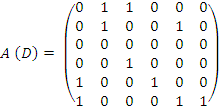
Сумма всех элементов i-ой строки равна числу равна числу дуг, выходящий из вершины v_i; сумма всех элементов j-го столбца равен числу дуг, направленных в вершину v_j. Если А – матрица смежност орграфа D, то элемент матрицы Aⁿ, стоящий в i-ой и ом столбце, будет равен числу путей (не обязательно оргцепей и простых оргцепей) длины n, идущих из вершины v_i в вершину v_j.

Легко видеть, что матрица B=A² = AA составлена из целых чисел b_ij, которые равны числу путей длины 2, соединяющих вершины i и j. Понятно, что А³ составлена из чисел, равных числу путей длины 3 (т.е. путей из 3-х ребер) из вершины i в вершину j и т.д.

Матрица инциденций – это матрица размера nхm, где n – число вершин, а m- число ребер графа, при этом ее элементы k_ij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер

Матрица B(G)определяет граф Gс точностью до изоморфизма.

Пример 8. Для графа G изображенного на рис. 1.8 матрица B(G) приводится в табл. 1.1

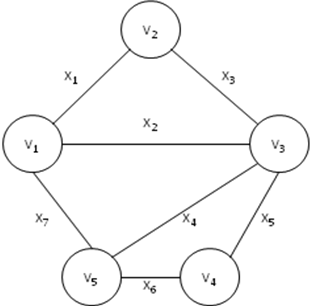
Рис. 7

Таблица 1

	x1	x2	x3	x4	x5	x6	x7
v1
v2
v3
v4
v5

Матрицей инцидентности орграфа D называется (nxm) – матрица B(D)=(b_ij), у которой:

Пример 9. Для орграфа D, изображенного на рис. 8, матрица B(D) приводится в табл. 2

Рис. 8

Таблица 2

	x1	x2	x3	x4
v1	-1
v2		-1		-1
v3			-1

По матрице смежности графа (орграфа) всегда можно определить ребра графа (дуги орграфа) как пары инцидентных им вершин, а для псевдографов, кроме того, и кратности ребер (дуг). Однако, если ребра (дуги) были пронумерованы, то восстановить их номера по матрице смежности невозможно невозможно. В этом смысле матрица инцидентности оказывается более информативной, чем матрица смежности, поскольку позволяет получить точную информацию о ребра (дугах), включая их нумерацию.

Заметим, что матрица инциденций сравнительно редко используется, так как в современных условиях (где число ребер часто очень велико) она имеет слишком большое число столбцов.

Пример 10. Для неориентированного графа, изображенного на рис. 9,постройте матрицу смежности и матрицу инцидентности.

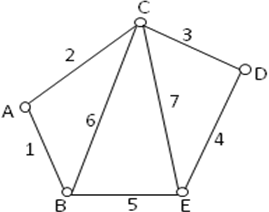рис.9

Решение. Матрица смежности

A B C D E

Матрица инцидентности

1 2 3 4 5 6 7

Структурная матрица. Именно эта матрица имеет особое значение в теории сетей связи. Структурная матрица – это символьная матрица порядка n. Она составляется следующим образом: на главной диагонали стоит 1, т. е. a_ij =1, остальные элементы – это символьные обозначения ребер (если вершины i и j не соединены ребром, то a_ij =0). При этом, если при i<j вершины i и j соединены ребром a, то элемент s_ij=a, при i>j – это отрицание a, которое обычно отмечаться чертой сверху. Если связи вершины i с вершиной j нет, то соответствующий элемент равен 0, структурная матрица может составляться и для орграфа и для мультиграфа без петель (здесь если два ребра a и b соединяются две вершины, то соответствующий элемент при i <j равен a v b, а при i>j этот элемент равен ).

Теорема. Для того чтобы найти все пути (прости) из вершины i в вершину j достаточно раскрыть минор M(j,i) структурой матрицы методами булевой алгебры. При этом раскрытие минора производится обычными действиями с определителями, но при этом сложение заменяется дизъюнкцией, умножение – конъюнкцией, знаки умножения на числа не используются.

Пример 11. Пусть дан ориентированный граф (рис. 10), причем ребра a, b, h являются ориентированными (их направление указано стрелками), а остальные ребра не ориентированы. Требуется методами булевой алгебры найти пути и сечения между вершинами 2 и 4.

Рис. 10

Составляем структурную матрицу Sзатем вычеркиваем из нее 4-ю строчку и 2-й столбец (тем самым получаем минор M(4,2)):

,

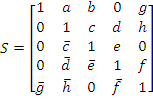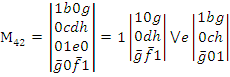
Раскрытие определителей производится по известному правилу: определитель равен сумме (в данном случае дизъюнкции) произведений элементов, умноженных на свои алгебраические 3-го порядка можно пользоваться и правилом треугольника.

Тогда получаем

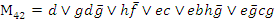
Искомые пути, расположенные в порядке прохождения ребер:

Сечения же получатся отрицанием этих путей. Применяя правила да\е Моргана (заменяя конъюнкцию на дизъюнкцию и наоборот), затем раскрывая скобки, получаем: (знаки отрицания опущены во всех равенствах, кроме 1-го):

,

или, применяя в скобках правило поглощения, получаем

ГЛАВА IV. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Дата добавления: 2014-11-07