
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные законы, определяющие свойства введенных логических операций
|
|
|
|
1) Идемпотентность дизъюнкции и конъюнкции:
X  X↔X, X
X↔X, X  X↔X.
X↔X.
2) Коммутативность дизъюнкции и конъюнкции:

3) Ассоциативность дизъюнкции и конъюнкции:

4) Дистрибутивность операций дизъюнкции и конъюнкции относи
тельно друг друга:
 5) Двойное отрицание:
5) Двойное отрицание:

6) Закон де Моргана:
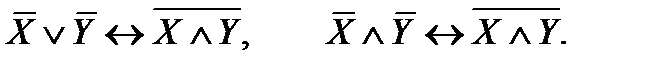
7) Склеивание:
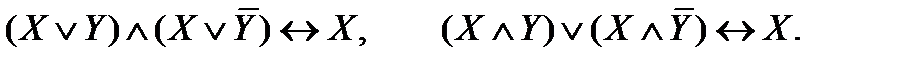 .
.
8) Поглощение:
 .
.
9) Действие с логическими константами 0 и 1:
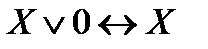 ,
, 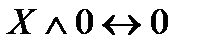 ,
,  ,
, 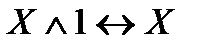 ,
, 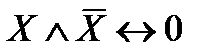
10) Закон исключения третьего:
 .
.
11) Тождество:
Х↔Х.
12) Отрицание противоречия:
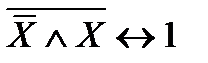 .
.
13) Контрапозиция:
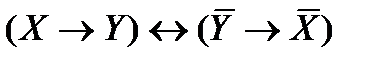 .
.
14) Цепное заключение:
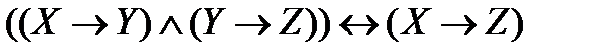 .
.
15) Противоположность:
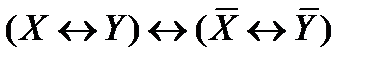 .
.
16) Модус поненс (modus ponens):
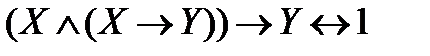 .
.
Сформулированные законы легко проверить с помощью таблицы истинности.
Заметим, что при исследовании различных высказываний на эквивалентность (равносильность) логическую связку ↔ можно заменить обычным знаком равенства =.
Задача. Составьте таблицу истинности формулы:  .
.
Решение. Расставим скобки:  .
.
| X | Y | Z | 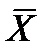
| 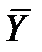
| 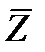
|  ХфУ ХфУ
| 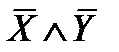
| 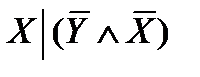
| 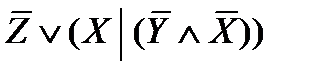
| 
|
| ] |
Задача. Докажите тождественную истинность формулы 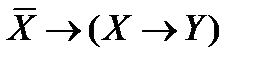 .
.
Решение. Составим таблицу истинности:
| X | Y | 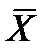
| 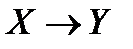
| 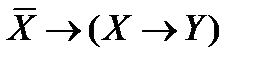  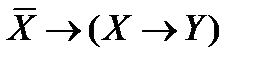
|
Последний столбец состоит из 1, следовательно, доказана тождественная истинность формулы.
Задача. Проверьте, будут ли эквивалентны следующие формулы:
а)  ; б)
; б) 
Решение. Составим таблицы истинности:
| X | У | Z |  Y@z Y@z
| 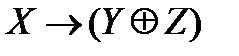 X -> (У (В Z) X -> (У (В Z)
| 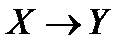
| 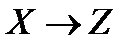
| 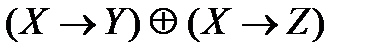
|
Формулы не эквивалентны.
| X | У | Z | 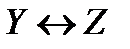 Y^Z Y^Z
| 
| 
| 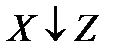
| 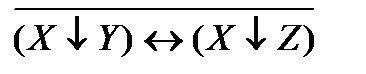
|
Формулы эквивалентны.
Булева функция, или функция алгебры логики, является одним из основных объектов дискретной математики.
Функцию f(x1, x2,…,хп), принимающую одно из двух значений 0 или 1, от п переменных, каждая из которых принимает одно из двух значений О или 1, будем называть булевой функцией f(x1, x2,…,хп) от п переменных.
Булева функция от п переменных сопоставляет каждому упорядоченному набору (кортежу), составленному из п элементов, 0 и 1, либо 1, либо 0.
Две булевы функции называются равными, если для любых одинаковых наборов значений переменных обе функции принимают одинаковые значения. Булевых функций одной переменной четыре, а двух переменных — шестнадцать и т. д. Число булевых функций от п переменных равно 22n.
Рассмотрим функции одной и двух переменных, которые называются «элементарными» функциями и с помощью которых можно определить функции большего количества переменных.
Таблица истинности булевой функции одной переменной:
| X | f1(x) | f2(x) | f3(x) | f4(x) |
Функции f1(x) и f4(x) называются константами — соответственно 0 и1.
Функция f2(x) совпадает с переменной х и называется тождественной f2(x) = х:
Функция f3(x) принимает значения, противоположные значениям аргумента х, и называется отрицанием х, обозначается  х: f3(x) =
х: f3(x) =  .
.
Таблица истинности булевой функции двух переменных:
| x1 | х2 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | f16 |
| i | l | ||||||||||||||||
| l | |||||||||||||||||
Следует отметить, что здесь к функциям двух переменных относятся и такие, которые в действительности зависят от одной переменной.
1. Функции f1 и f16 представляют собой константы 0 и 1.
2. Функции f4, f6 , f11,f13 существенно зависят только от одной переменной: f4=x1,. f6=x2, f11= 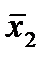 , f13=
, f13= 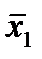
3. Остальные функции существенно зависят от двух переменных, и для них есть названия и обозначения:
а) функция 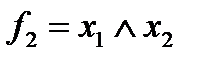 называется конъюнкцией,
называется конъюнкцией,
б) функция  называется дизъюнкцией,
называется дизъюнкцией,
в) функция  называется эквивалентностью,
называется эквивалентностью,
г) функция 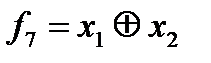 называется суммой по модулю два, или суммой Жегалкина,
называется суммой по модулю два, или суммой Жегалкина,
д) функция / 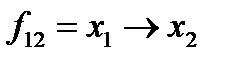 называется конверсией,
называется конверсией,
е) функция 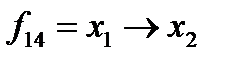 называется импликацией,
называется импликацией,
ж) функция  называется штрих Шеффера,
называется штрих Шеффера,
з) функция 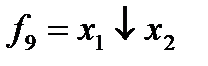 называется стрелкой Пирса,
называется стрелкой Пирса,
и) функции 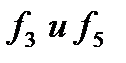 логически несовместимы с импликацией и конверсией и называются функциями запрета.
логически несовместимы с импликацией и конверсией и называются функциями запрета.
|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 2795; Нарушение авторских прав?; Мы поможем в написании вашей работы!