Метод расчета коэффициента внутреннего трения

Выполнение работы

Жидкости методом Стокса

Определение коэффициента внутреннего трения

1. Цель работы: определение коэффициента внутреннего трения жидкости методом Стокса.

2. Оборудование: цилиндр с исследуемой жидкостью, шарик, микрометр, линейка, секундомер, магнит.

3. Подготовка к работе: а) изучить необходимые теоретические положения по учебникам: [1] § 48; [2] 10.7, 10.8; [3] §§ 39–43, 79; б) ответить на вопросы для самоподготовки 1–17; в) уметь пользоваться измерительными приборами.

Для выполнения работы студент должен знать: а) явления переноса (диффузия, внутреннее трение, теплопроводность) и уравнения, описывающие эти неравновесные процессы; б) методику расчета коэффициента внутреннего трения жидкости, его физический смысл; в) физический смысл числа Рейнольдса и различие между ламинарным и турбулентным течением; г) порядок расчета абсолютной и относительной погрешностей при прямых и косвенных измерениях.

В трубах при движении жидкости различные слои жидкости движутся с разными скоростями, причем, чем дальше слой от стенки сосуда, тем его скорость больше. При этом слой жидкости с большей скоростью увлекает рядом находящийся слой, движущийся с меньшей скоростью. Слой же с меньшей скоростью, в свою очередь, действует на слой, движущийся с большей скоростью, и тормозит его, то есть происходит обмен импульсом соседних слоев.

При установившемся движении скорости слоев остаются постоянными. Силу, с которой один слой жидкости действует на другой, называют силой внутреннего трения. Величина силы внутреннего трения зависит от разности скоростей движения слоев, от расстояния между слоями и площади их соприкосновения.

Эта зависимость выражается формулой

,

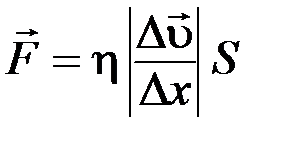где 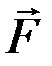– сила внутреннего трения; h – коэффициент внутреннего трения; – разность скоростей слоев, отстоящих на расстояние ; 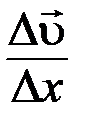– градиент скорости, характеризующий быстроту ее изменения в указанном направлении; – площадь, на которую действует сила трения.

Коэффициент внутреннего трения может быть определен из наблюдений за движением шарика в вязкой среде (метод Стокса).

На шарик (рис. 1), движущийся в вязкой среде, действуют силы:

1) направленная вниз сила тяжести

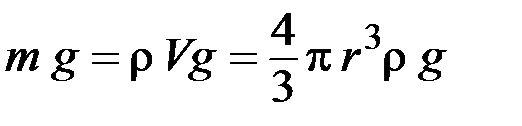, (1)

где m – масса шарика; – его объем; 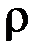– плотность материала шарика; g – ускорение свободного падения;

2) направленная вверх сила Архимеда

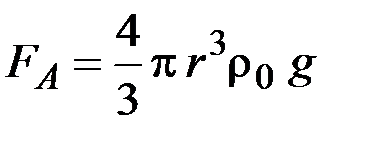, (2)

где – плотность жидкости;

3) cила сопротивления среды, обусловленная вязкостью жидкости, направлена в сторону, противоположную скорости движения шарика.

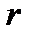Согласно формуле, выведенной Стоксом, сила внутреннего трения пропорциональна скорости шарика, его радиусу и коэффициенту 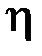внутреннего трения (динамической вязкости):

. (3)

Эта формула справедлива для движущегося в жидкости твердого шарика при условии, что скорость его невелика, а расстояние до границ жидкости значительно больше диаметра шарика.

Основное уравнение поступательного движения шарика записывается в виде:

. (4)

В проекции на ось Х (см. рис. 1) с учетом равенств (1–3) уравнение (4) примет вид:

. (5)

Сила сопротивления 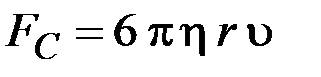зависит от скорости и при некотором ее значении движение шарика становится равномерным, то есть выполняется соотношение:

, (6)

где – скорость установившегося равномерного движения; 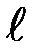– расстояние между метками на цилиндре с жидкостью; – время равномерного движения шарика.

Из уравнения (6) с учетом соотношения для определения скорости 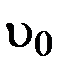равномерного движения находят коэффициент внутреннего трения исследуемой жидкости:

. (7)

Дата добавления: 2014-11-07