Формула Бернуллі

Формула Бернуллі

Якщо проводяться випробування, при яких ймовірність появу події А в кожному випробуванні не залежить від результатів інших випробувань, то такі випробування називають незалежними відносно події А. У § 1-4 ці розділи розглядаються незалежні випробування, в кожному з яких ймовірність появи події однакова.

Ймовірність того, що в n незалежних випробуваннях, в кожному з яких ймовірність появи події рівна р(0 < р < I), подія відбудеться рівно k раз (байдуже у якій послідовності), дорівнює

,

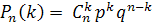або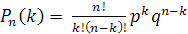

де q=1-р

Ймовірність того, що в n випробуваннях подія наступить: а) менше k раз; б) більш k раз; в) не менше k раз; г) не більш k раз, - знаходять відповідно за формулами:

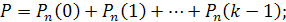
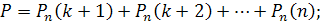
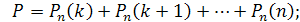
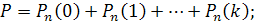
50. Два рівносильні шахісти грають в шах мати. Що ймовірніше: виграти дві партії з чотирьох або три партії з шести (нічиї до уваги не приймаються)?

Розв’язання. Грають рівносильні шахісти, тому ймовірність виграшу р = 1/2; отже, ймовірність програшу q також рівна 1/2. Оскільки у всіх партіях ймовірність виграшу постійна і байдуже, в якій послідовності будуть виграні партії, то застосовна формула Бернуллі. Знайдемо ймовірність того, що дві партії з чотирьох будуть виграні:

P₄ (2) =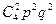= = 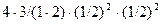6/16.

Знайдемо вірогідність того, що буде виграно три партії з шести:

Р_n (3)=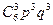==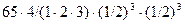5/16.

Оскільки Р₄ (2) > P₆ (3), то ймовірніше виграти дві партії з чотирьох, чим три з шести.

51. Монету кидають п’ять разів. Знайти ймовірніше того, що «герб» випаде: а) менше двох разів; б) не менше двох разів.

52. Знайти ймовірність того, що подія А появиться не менше трьох раз в чотирьох незалежних випробовуваннях, якщо ймовірність появи події А в одному випробовуванні рівна 0,4;

а) подія В з’явиться у випадку, якщо подія А відбудеться не менше чотирьох раз. Знайти ймовірність настання події 5, якщо буде проведено п’ять незалежних випробувань, в кожному з яких ймовірність появи події А = 0,8.

Дата добавления: 2014-10-15