
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дотична площина та нормаль до поверхні
|
|
|
|
Озн.1 Дотичною площиною до поверхні в точці М називається площина, яка має у собі усі дотичні до кривих, проведених на поверхні через точку М
Якщо поверхня задана рівнянням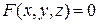 , то рівняння дотичної площини в точці М(хо;уо) до поверхні має вигляд:
, то рівняння дотичної площини в точці М(хо;уо) до поверхні має вигляд:
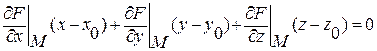 (1)
(1)
Якщо поверхня задана рівнянням  , то рівняння (1) має вигляд:
, то рівняння (1) має вигляд:
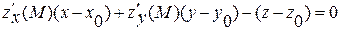
Озн.2 Нормаль до поверхні - це пряма, яка проходить через точку дотику і перпендикулярна дотичній площині.
Якщо поверхня задана рівнянням 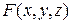 , то канонічне рівняння нормалі має вигляд:
, то канонічне рівняння нормалі має вигляд:
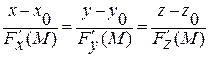
Якщо поверхня задана рівнянням  , то
, то 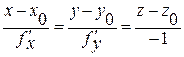 .
.
Приклад: Знайти рівняння дотичної до нормалі в точці М(1;1;1) 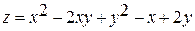 .
.
Розв’язання:
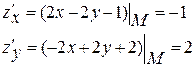
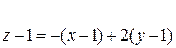
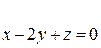
Нормаль: 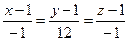
Невизначений інтеграл
§1 Первісна та невизначений інтеграл
Означення 1. Функція F(x) називається первісною для даної функції f(x) на проміжку (а; b), якщо 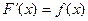 для будь-яких (
для будь-яких (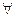 )
)  .
.
Теорема 1. Якщо F1(x) і F2(x) – дві первісні для функції f(x) на проміжку
(а; b), то різниця між ними дорівнює сталому числу.
Доведення. Нехай f(x) існує на проміжку (а; b), та F1(x) і F2(x) її первісні. Тобто, за означенням 1 маємо 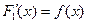 та
та 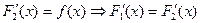 .
.
За наслідком з теореми Ла-Гранжа маємо F1(x) - F2(x) =с, де с = const.
Тобто, 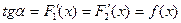 .
.
(М1; М2)=с, с = const.
Наслідок. Якщо F(x) первісна для деякої функції f(x) то будь-яка інша первісна має вигляд F(x)+С.
Означення 2. Сукупність всіх первісних для функції f(x) називається невизначеним інтегралом від функції f(x) і позначається символом 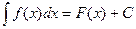 , де
, де
f(x) – підінтегральна функція,
f(x)dx – підінтегральний вираз,
∫ - знак інтеграла.
Операція знаходження первісної для даної функції f(x) називається інтегруванням. Крива F(x) називається інтегральною кривою.
§2 Властивості невизначеного інтеграла
1. 
2. 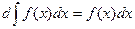
3. 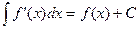
4. 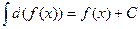
5.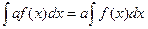 , де
, де 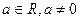
6. 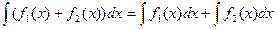
Знаки d i ∫ слідуючи один за одним в будь-якій послідовності взаємознищуються.
Доведемо 5 властивість.
Нехай F(x) – первісна f(x). За означенням 2 маємо
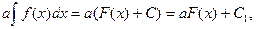
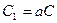
Тоді аF(x) є первісною для функції аf(x).
Дійсно, за означенням 1  .
.
§3 Таблиця невизначених інтегралів
Нехай х – незалежна змінна, функція f(x) неперервна на даному інтервалі і F(x) – її первісна.
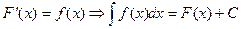 (1)
(1)
Нехай 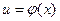 , де
, де 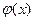 - неперервна і диференційована, а
- неперервна і диференційована, а 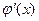 - неперервна і розглянемо
- неперервна і розглянемо
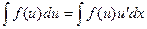 (2)
(2)
В даному випадку складена функція 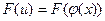 є первісною для підінтегральної функції (2). Тоді знайдемо
є первісною для підінтегральної функції (2). Тоді знайдемо
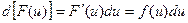
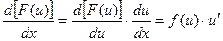
Це означає
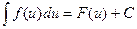 , (3)
, (3)
де 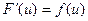 .
.
Тобто, мають місце (1) і (3).
Зауваження
Деякі перетворення диференціалів
1)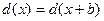 , де
, де 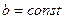
2) ,
, 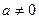
3) 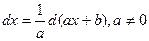
4) 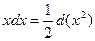
5) 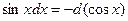
6) 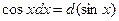
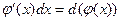
§4 Методи інтегрування
1. Підведення під знак диференціалу
Нехай потрібно знайти інтеграл від функції 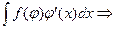 . За означенням диференціалу функції вираз
. За означенням диференціалу функції вираз 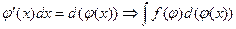 .
.
Приклад.
Обчислити інтеграл 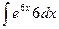 ,
, 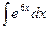
2. Інтегрування за частинами
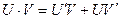

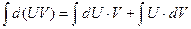

 - інтегрування за частинами
- інтегрування за частинами
Приклад
1. 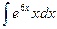
2. 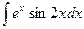
3. Інтеграл від функції, що містить повний квадрат
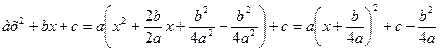
Розглянемо 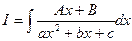 (2)
(2)
він зводиться до інтегралу (1) шляхом виділення в чисельнику похідної від знаменника
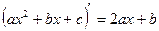
Приклад: 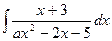
4. Інтегрування раціональних дробів.
Розглянемо правильний дріб 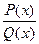
Нехай для визначенності 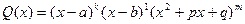 (2), де квадратичний тричлен не має дійсних коренів.
(2), де квадратичний тричлен не має дійсних коренів.
Теорема. Правильний раціональний дріб 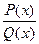 , де
, де 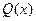 - (2) можна єдиним способом розкласти на суму найпростіших дробів.
- (2) можна єдиним способом розкласти на суму найпростіших дробів.
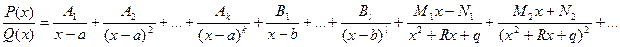
(3)
Метод невизначених коефіцієнтів.
Коефіцієнти Аі, Ві, Мі, Nі – в рівності (3) можна визначити слідуючим чином. Рівність (3) – це тотожність, тому звівши дроби (3) до спільного знаменника, отримаємо тотожні многочлени в чисельниках зліва та справа. Порівнюючи коефіцієнти при однакових степенях – x, або даючи х значення отримаємо систему рівнянь для визначення отримаємо систему рівнянь для визначення невідомих коефіцієнтів.
Це є метод невизначених коефіцієнтів.
Приклад: 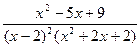
Зауваження: Всі неправильні дроби перетворюються у правильні діленням многочлена на многочлен, тобто виділяючи цілу частину.
Приклад: 
§ 5 Інтегрування деяких ірраціональних функцій
1)  dx, a
dx, a
2) 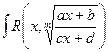 dx
dx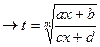
3) 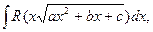 де
де 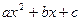 не має рівних коренів. Якщо D< 0, а >0
не має рівних коренів. Якщо D< 0, а >0 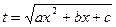
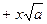 - перша підстановка Ейлера.
- перша підстановка Ейлера.
D>0, 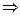
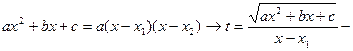 друга підстановка Ейлера
друга підстановка Ейлера
§ 6 Інтегрування тригонометричних функцій
1. 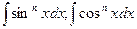 n – цілі, >0
n – цілі, >0
а) n – парне: 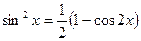

б) n – непарне sin x або cos x підвести під знак диференціалу і використовують тригонометричні формули
Приклади: 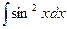 ,
, 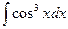
2. 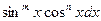 ,
,
а) m,n – хоча б одне непарне, виділити один множник і замінюючи змінну на t, отримаємо табличні інтеграли.
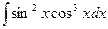
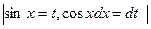
б) m, n – парне > 0 – знижувати степінь за тригонометричними формулами
3. 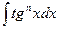
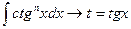
Приклади: 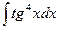
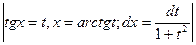
4. 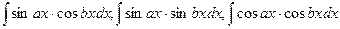
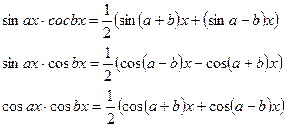
5. 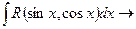 універсальна підстановка
універсальна підстановка 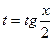 ;
;
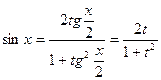
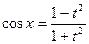
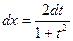
Приклад: 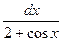
§ 7 Інтегрування функцій, раціонально залежних від тригонометричних
1) 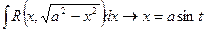 або
або
Приклад: 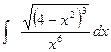
2)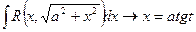
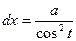
3) 
Зауваження 1. 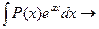
Інтегрування за частинами

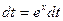
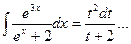
Зауваження 2. Існують інтеграли, які не мають рішення ні за одним з вказаних методів. Вони знаходяться лише за приблизними правилами.
Наприклад: 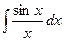
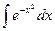
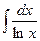 і т. д.
і т. д.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 1563; Нарушение авторских прав?; Мы поможем в написании вашей работы!