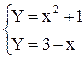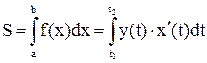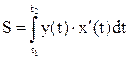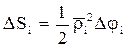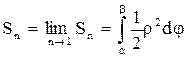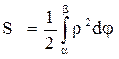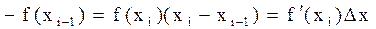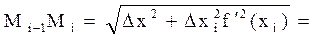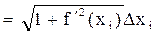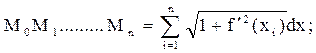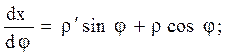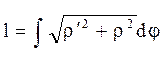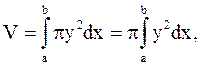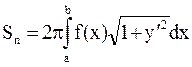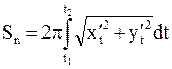КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометричні застосування визначеного інтегралу
|
|
|
|
Наближені обчислювання визначених інтегралів
1.Формула прямокутників
 , n-кількість інтервалів Δxi
, n-кількість інтервалів Δxi




 y
y
 |
 Δxi x
Δxi x
a b
2.Формула трапецій
 , n-кількість інтервалів Δxi
, n-кількість інтервалів Δxi
 |
y
 |
Δxi
 |
a b x
3.Формула парабол (Симпсона)

 y
y
 x
x
a b x
Приклад: 
Обчислити беспосередньо та за формулами прямокутників,
трапецій та парабол. Оцінити похибку



розіб’ємо інтервал 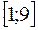 на вісім частин, з кроком h=1
на вісім частин, з кроком h=1
| I | |||||||||
| X | |||||||||
| y | 1,0000 | 2,6458 | 3,6056 | 4,3589 | 5,0000 | 5,5678 | 6,0828 | 6,5574 | 7,0000 |
Формула прямокутників



абсолютна похибка Δ=│38-34,8183│=3,1817, відносна 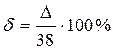

Формула трапецій

похибка:
 Δ=│38-37,8183│=0,1817
Δ=│38-37,8183│=0,1817

Формула Симпсона

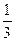 (8+4·19,1299+
(8+4·19,1299+
+2·14,6884) 37,9655
37,9655

 Δ= 38-37,9655 =0,0345
Δ= 38-37,9655 =0,0345

Отже меншу похибку дав метод Симпсона
1.Площа в прямокутних кординат ax
На основі геометричного змісту визначеного інтегралу площа криволінійної
трапеції a ABb, обмеженою зверху неперервною кривою y=f(x), f(x)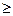 0
0
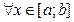 , вертикалю х= a та х=b і віссю ОХ
, вертикалю х= a та х=b і віссю ОХ
S = (1)
(1)
Якщо 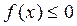
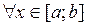 ,
, 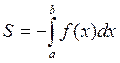
 Якщо f(x) міняє знак скінчене число раз на проміжку [ a,b ] то інтеграл по [a;b] розбиваємо на суми інтегралів по частинними відрізкам. Щоб отримати площу потрібно знайти суму абсолютних величин інтегралів по всім відрізкам.
Якщо f(x) міняє знак скінчене число раз на проміжку [ a,b ] то інтеграл по [a;b] розбиваємо на суми інтегралів по частинними відрізкам. Щоб отримати площу потрібно знайти суму абсолютних величин інтегралів по всім відрізкам.
|




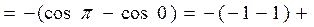

|

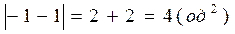

 В більш складних випадках фігуру представляють у вигляді суми або різниці криволінійних трапецій.
В більш складних випадках фігуру представляють у вигляді суми або різниці криволінійних трапецій.
 |
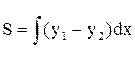
|
Визначити площу S обмежену параболою
 Y=x2+1 та x+y=3
Y=x2+1 та x+y=3
|
|
|
1.Визначимо межі інтегрування
|
| ||||
|
Якщо криволінійна трапеція обмежена кривою, яка задана параметрично х=х(t); y=y(t) tÎ[t1 ; t2]
|
|
|
|
 1.Визначимо межі інтегрування
1.Визначимо межі інтегрування
|
 Якщо криволінійна трапеція обмежена кривою, заданою в полярних координатах ρ=ρ(φ),
Якщо криволінійна трапеція обмежена кривою, заданою в полярних координатах ρ=ρ(φ),
φÎ [ α;β ]. Визначимо площу. Нехай в полярній системі координат маємо криву ρ=ρ(φ), де ρ(φ) неперервна функція на [ α;β ]. Визначимо площу сектора, обмеженого кривою ρ=ρ(φ) та радіус-векторами φ 1=α, φ 2=β. Розіб’ємо дану площу радіус-векторами на n частин, позначимо через Δ φ 1,Δ φ 2,..., Δ φ n кути між проведеними радіус-векторами
 i – довжина радіус-вектора,що відповідає будь-якому куту φ і, що знаходяться між φ і-1 та φ і.Площа кругового сектора з радіусом ρі та центральним кутом Δ φ і
i – довжина радіус-вектора,що відповідає будь-якому куту φ і, що знаходяться між φ і-1 та φ і.Площа кругового сектора з радіусом ρі та центральним кутом Δ φ і
| |||
| |||
, тоді
|
|
при n®¥ маємо
|
Обчислити площу обмежену лінією
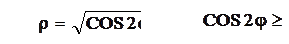 | |||
 | |||
;
| j | -p/4 | p/4 | |
| r |
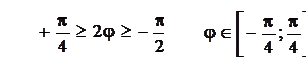 | |||
|
2. Довжина дуги плоскої кривої
 |
Під довжиною дуги АВ розуміють границю до якої прямує довжина ламаної, вписаної в цю дугу, коли число частин ламаної необмежено зростає, а довжина найбільшої частини прямує до нуля.
 Нехай y=f(x) рівняння кривої на [a;b]
Нехай y=f(x) рівняння кривої на [a;b]
Розіб’ємо криву точками Мі на n частин, маємо М0М1... Мn -ламану.
Довжина Мі-1 Мі буде дорівнювати:
 |
|
|
|
|
|
|
|
при n®¥
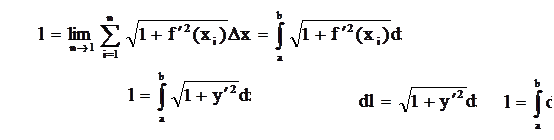 |
 або, якщо
або, якщо
|
Обчислити довжину кола x2+y2 = r2, y= r2-x2
 |
Якщо дуга кривої задана параметрично x=x(t), y=y(t), tÎ[t1;t2]

|
| |||
|
 Обчислити довжину дуги x = a cos3 t, y = a sin3t
Обчислити довжину дуги x = a cos3 t, y = a sin3t
 | |||
|
Межі інтегрування знайдемо надаючи параметру f значення:
| t | p/3 | p/2 | |
| x | a | 0.35a | |
| z | 0.35a | A |
|
|
|
| |||
|
Приклад
|
Обчислити довжину кардіоїди
 |
| j | p/3 | p/2 | p | |
| r | 2a | 1.5a | a |

3. Обчислення об’єму тіла за площею паралельних перерізів
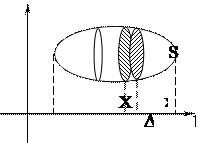 |
Нехай задано тіло Т, та відомо площу будь-якого перерізу цього тіла площиною,перпендикулярною до осі ОХ. Ця площа залежить від положення січної площини і являється функцією від Х: S=S(x). необхідно визначити об’єм тіла Т, якщо S(x) — неперервна
функція. Спроектуємо тіло на вісь ОХ,
отримаємо [a;b], який дає лінійний розмір тіла в напрямку ОХ, розділимо [a;b] точками xi на n частин і через них проведемо площини, перпендикулярні ОХ, тіло розіб’ється на суму циліндрів, об’єми яких
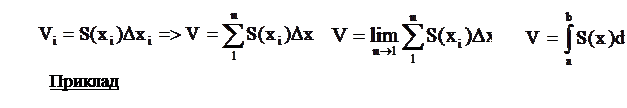
 Знайти об’єм піраміди з площею основи та висотою Н. Нехай S(x) — площа перерізу. Площі їх перерізів відносяться як квадрати їх відстаней до вершини.
Знайти об’єм піраміди з площею основи та висотою Н. Нехай S(x) — площа перерізу. Площі їх перерізів відносяться як квадрати їх відстаней до вершини.
| |||
| |||
;
|
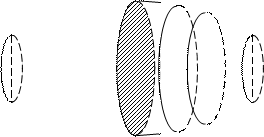
4.Об’єм тіла обертання.
|
|
|
|
|





|

|

|
|
|
|
та прямими x=a, x=b.
S(x)= py2 — коло в розрізі
|
аналогічно
|
|
|
Отже
|
Визначити об‘єм тіла.
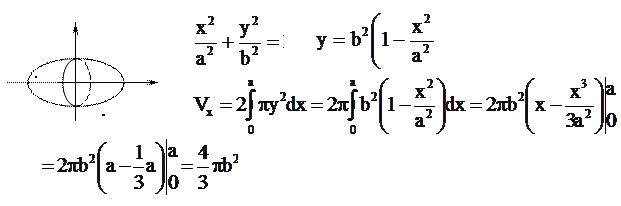 |
|
|
|



 Y=f(x)обертається навколо осі ОХ на [a;b]
Y=f(x)обертається навколо осі ОХ на [a;b]
|



|
 |
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 887; Нарушение авторских прав?; Мы поможем в написании вашей работы!