Поняття визначеного інтегралу

Семестр

РОЗДІЛ 1

ВИЗНАЧЕНИЙ ІНТЕГРАЛ

Нехай f(х)=у неперервна на х [ a, b ]

y aABb - криволінійна трапеція.

B відшукаємо її плошу.

Для цього [ a, b ] розіб’ємо точками на n рівних

частин. Точки m i M_i – є min та max f (x) -

інтервалу [x_i, x_i+1],

A aABb - розіб’ється на частини, площа і-ої

частини більше або дорівнює m (x_i+1 –x_i) менше

0 a x₁ x₂ b x або дорівнює М_і(х_і+1 – х_i).

Нехай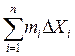 Sn= S'n=

Sn S_aАВb S'n,т.ч. Sn i S'n прямують до S_aABb, коли n

Означення Нехай f (x), x [ a; b ] - неперервна невід’ємна функція, а

границі послідовностей Sn i S'n існують і рівні, їх

значення називають площиною криволінійної трапеції.

Таким чином, нехай с_і (х_і-1, х_і) тоді m_i ≤ f (c_i) ≤ M_i домножемо його

на Δx_i та знайдемо суму усіх значень від 1 до n

Sn ≤ f (c_i) _∆x_i ≤ S’n, →

Означення Нехай f (x) визначена в будь-якому х [ a; b ]. Якщо

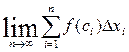існує і не залежить від вибору т. с_і , то f (x)

називають інтегрованою на проміжку [ a; b ], а границю -

визначеним інтегралом від функції f (x) на [ a; b ] і

позначають

Властивості:

1.Для будь-якого числа α: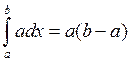

2. Якщо f (x) інтегрована на [ a; b ], то α ф-я α f (x) також інтегрована

на [ a; b ]: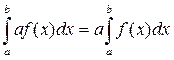

3. Інтеграл суми дорівнює сумі інтегралів, якщо ф-ії f (x) i g (x)

інтегровані на [ a; b ],

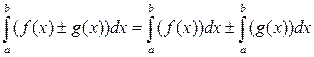
4. Якщо f (x) i g (x) інтегровані на [ a; b ] i f (x) ≤ g (x), то

5. Для інтегрованої функції f (x) на проміжку [ a; b ] виконується:

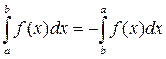
6. Якщо f (x) інтегрована на [ a; b ], то вона інтегрована на проміжку

[ a; b ] крім того, якщо f (x) інтегрована на [ a; c ] i [ c; d ], то вона

інтегрована на проміжку [ a; b ]

Доведення: Нехай a < c < b, так як границя інтегрованної суми не

залежить від способу ділення відрізка [ a; b] то будемо ділити його таким

чином,щоб точка С була точкою ділення, наприклад: C=Xm,тоді

інтегральна сума розіб’ється на дві суми:

переходячи до границі, коли отримаємо:

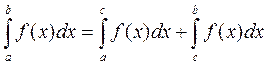
Якщо a, b, c розташовані іншим чином, наприклад a < b < c, властивість

зберігається, дійсно:

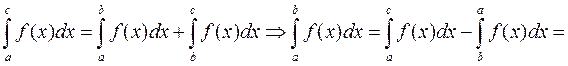
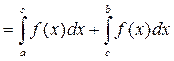
7. Якщо інтегрована на проміжку [ a; b] функція f(x) задовільняє нерівності

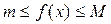, де m, M = const, відповідно min та max на [ a; b] то

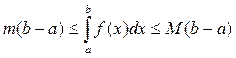
8.Якщо f(x) інтегрована на проміжку [ a; b], то

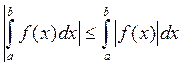
Дата добавления: 2014-10-15