I. Дифференциальные уравнения 1-го порядка

Контрольная работа

III. Системы обыкновенных дифференциальных уравнений.

Литература: 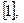гл. ХIII §29 упр. 180, §30 упр. 185, 186, 188, гл.ХХI §17 упр. 14.

Вопросы для самопроверки.

1. Дайте определение: а) нормальной системы ДУ 1 порядка; б) однородной системы в нормальной форме. Сформулируйте задачу Коши для этой системы.

2. Изложите метод исключения решения нормальной системы ДУ 1 порядка.

3. Изложите метод нахождения общего решения нормальной системы 2-х линейных однородных ДУ с постоянными коэффициентами в случае простых корней характеристического уравнения.

4. Запишите в матричной форме нормальную систему и решение нормальной системы 2-х линейных однородных ДУ с постоянными коэффициентами.

Рассмотрим 2 примера решения дифференциального уравнения 1-го порядка:

а) однородного; б) линейного.

а) Однородное дифференциальное уравнение 1-го порядка .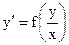

Пример 1. Проинтегрировать дифференциальное уравнение

.

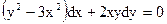Решение. Данное уравнение – однородное, т.к. выражения, стоящие перед dx и dy являются однородными функциями одного и того же измерения, а именно 2-го измерения. Действительно,

;

.

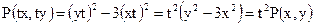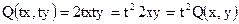Для интегрирования однородного уравнения удобнее разрешить его относительно производной :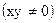

.

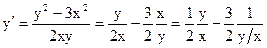Полагаем 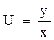, 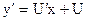. Подставим эти выражения в уравнение, тогда получим

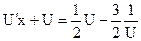или 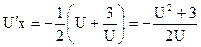- дифференциальное уравнение с разделяющимися переменными. Интегрируем его:

.

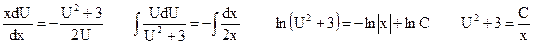Заменяем переменную U через ее значение :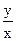

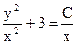или 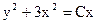- общий интеграл данного дифференциального уравнения.

б) Линейное дифференциальное уравнение 1-го порядка

(_*)

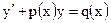может быть решено, например, методом Бернулли, согласно которому решение уравнения (_*) ищется в виде произведения 2-х функций, т.е.

.

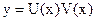Схема решения:

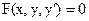
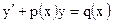
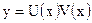
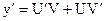
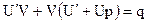
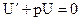
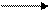
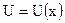
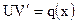
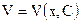
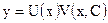
Пример 2. Решить уравнение

.

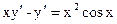Решение. Это уравнение – линейное, 1-го порядка, т.к. оно приводится к виду

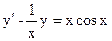
(у и у^/ содержатся в 1-х степенях, не перемножаясь друг с другом). Ищем решение этого уравнения. Положим 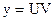, тогда

.

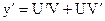Подставим у и у^/ в преобразованное уравнение и сгруппируем его члены:

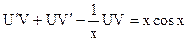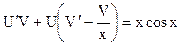, (3)

Выберем функцию V так, чтобы выражение, стоящее в скобках, обратилось в 0: .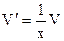

Получили уравнение с разделяющимися переменными

, ,

, , .

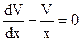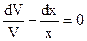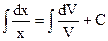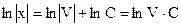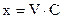Для простоты положим С=1. Тогда V=x. Подставим V=x (V^/=1) в уравнение (3) и последовательно находим

, , ,

, .

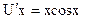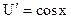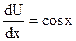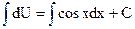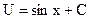Тогда решение дифференциального уравнения будет

.

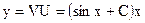Замечание 2. Некоторые уравнения становятся линейными, если поменять искомую функцию и независимое переменное. Например, уравнение 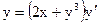запишем в виде

, .

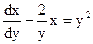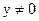Следовательно, это уравнение линейное относительно функции .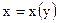

Задание №1 для контрольной работы^*.

Дата добавления: 2014-10-15