
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Даны дифференциальные уравнения 2-го порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям
|
|
|
|
2.1. 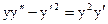
| 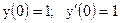
|
2.2. 
| 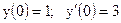
|
2.3. 
| 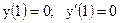
|
2.4. 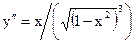
| 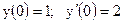
|
2.5. 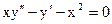
| 
|
2.6. 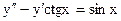
| 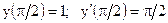
|
2.7. 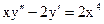
| 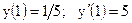
|
2.8. 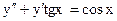
| 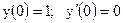
|
2.9. 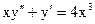
| 
|
2.10. 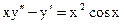
| 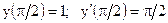
|
2.11. 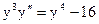
| 
|
2.12. 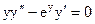
| 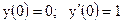
|
2.13. 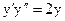
| 
|
2.14. 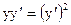
| 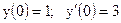
|
2.15. 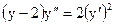
| 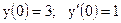
|
2.16. 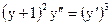
| 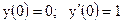
|
2.17. 
| 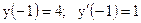
|
2.18. 
| 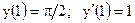
|
2.19. 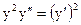
| 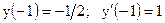
|
2.20. 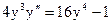
| 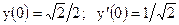
|
2.21. 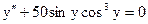
| 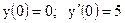
|
2.22. 
| 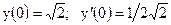
|
2.23. 
| 
|
2.24. 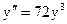
| 
|
3) Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами со специальной правой частью:
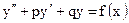 , (p, q – const) (1)
, (p, q – const) (1)
Общее решение уравнения (1)
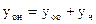 ,
,
где 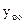 - общее решение линейного однородного дифференциального уравнения
- общее решение линейного однородного дифференциального уравнения
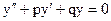 ,
,
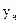 - некоторые частные решения уравнения (1).
- некоторые частные решения уравнения (1).
а) Рассмотрим решение ЛОДУ
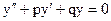 (2)
(2)
Схема решения (2):

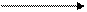
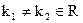
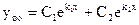 (3)
(3)



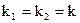
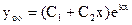 (4)
(4)

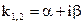
 (5)
(5)
Пример 1. Найти общее решение уравнений:
а) 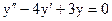 ;
;
б) 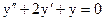 ;
;
в) 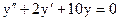 .
.
Решение.
а) составим характеристическое уравнение:
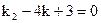 .
.
его корни 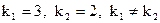 (1-ый случай). Общее решение исходного дифференциального уравнения будет согласно (3)
(1-ый случай). Общее решение исходного дифференциального уравнения будет согласно (3)
 .
.
б) Составим и решим характеристическое уравнение
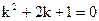 ,
,  (2-ой случай).
(2-ой случай).
Общее решение согласно (4) будет
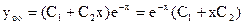 .
.
в) Составим и решим характеристическое уравнение
 ,
,  (3-ий случай).
(3-ий случай).
Общее решение согласно (5) будет
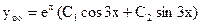 .
.
б) Решение ЛНДУ. Рассмотрим метод подбора частного решения (метод неопределенных коэффициентов). Этот метод применим только к линейным уравнениям с постоянными коэффициентами и только в том случае, когда его правая часть имеет вид
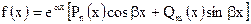 . (6)
. (6)
В этом случае частное решение ЛНДУ 2-го порядка
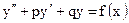
следует искать в виде
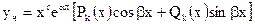 . (7)
. (7)
Здесь r равно числу совпадений контрольного числа  с корнями характеристического уравнения (
с корнями характеристического уравнения (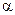 - показатель экспоненты,
- показатель экспоненты, 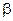 - коэффициент при х в тригонометрических функциях
- коэффициент при х в тригонометрических функциях 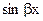 и
и  ).
). 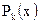 и
и  - полные многочлены от х с неопределенными коэффициентами, причем k равно наибольшему из чисел m и n в (6), при этом если в
- полные многочлены от х с неопределенными коэффициентами, причем k равно наибольшему из чисел m и n в (6), при этом если в 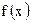 входит может быть одна из функций
входит может быть одна из функций 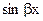 и
и  , то в (7) надо всегда вводить обе функции
, то в (7) надо всегда вводить обе функции 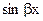 и
и  .
.
Частными случаями функции 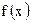 рассматриваемой структуры являются следующие функции:
рассматриваемой структуры являются следующие функции:
1. 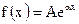 , А- постоянная,
, А- постоянная, 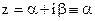 ;
;
2. 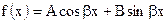 , А, В - постоянные,
, А, В - постоянные, 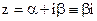 ;
;
3. 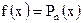 (многочлен степени n),
(многочлен степени n), 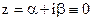 ;
;
4. 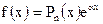 ,
, 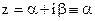 ;
;
5. 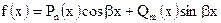 ,
, 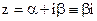 ;
;
6. 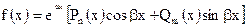 ,
,  .
.
Если правая часть исходного уравнения равна сумме нескольких различных функций рассматриваемой структуры (6), то для отыскания частного решения надо найти частные решения, соответствующие отдельным слагаемым правой части, и взять их сумму, которая и является частным решением исходного уравнения. Например,
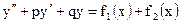 ,
,
тогда 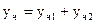 , где
, где 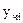 - частные решения уравнений
- частные решения уравнений
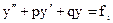
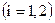 .
.
Пример 2. Решить уравнение
 .
.
Решение.
а) 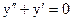 - ЛОДУ. Составим характеристическое уравнение
- ЛОДУ. Составим характеристическое уравнение 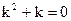 . Его корни
. Его корни
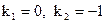 . Тогда
. Тогда 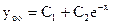 .
.
б) Составим по правой части 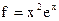 контрольное число
контрольное число  . Показатель экспоненты
. Показатель экспоненты 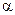 равен 1. Функций
равен 1. Функций  и
и 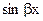
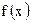 не содержит. Итак, контрольное число z будет равно 1. Следовательно, число совпадений
не содержит. Итак, контрольное число z будет равно 1. Следовательно, число совпадений  (т.к. совпадений
(т.к. совпадений  с корнями характеристического уравнения нет). Тогда частное решение будем искать в виде
с корнями характеристического уравнения нет). Тогда частное решение будем искать в виде
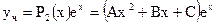 .
.
Дифференцируем 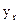 :
:
 .
.
Аналогично найдем
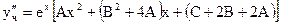 .
.
Подставляя 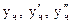 в исходное уравнение, получим
в исходное уравнение, получим
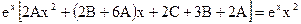 .
.
Это равенство выполняется при всех значениях х, а значит, коэффициенты при одинаковых степенях х в левой и правой частях равенства совпадают. Приравнивая эти коэффициенты, получаем:
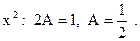
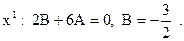
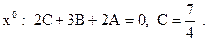
Таким образом,
 .
.
Пример 3. Составить вид частного решения следующих дифференциальных уравнений:
а) 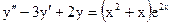 ;
;
б)  ;
;
в) 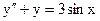 .
.
Решение.
а) Так как  ,
, 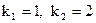 , то
, то
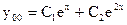 .
.
Частное решение следует искать в виде
 ,
,
т.к. r=1 (есть одно совпадение контрольного числа 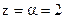 с корнем характеристического уравнения).
с корнем характеристического уравнения).
б) Так как 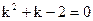 ,
, 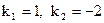 , то
, то
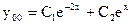 .
.
Контрольное число 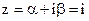 . Частное решение следует искать в виде
. Частное решение следует искать в виде 
(т.к. r=0, совпадений нет).
в) 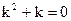
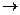
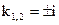
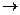
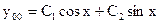 .
.
Так как 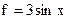 , то
, то 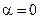 ,
, 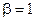 . Контрольное число
. Контрольное число  равно z=i; есть совпадение с корнем
равно z=i; есть совпадение с корнем  характеристического уравнения, следовательно, частное решение следует искать в виде
характеристического уравнения, следовательно, частное решение следует искать в виде
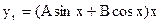 .
.
Задание №3 для контрольной работы*.
Найти:
а) частное решение линейного неоднородного уравнения 2-го порядка;
б) общее решение линейного неоднородного дифференциального уравнения.
3.1. а) 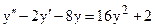 б)
б) 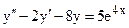
| 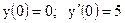
|
3.2. а)  б)
б) 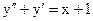
| 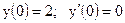
|
3.3. а) 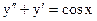 б)
б) 
| 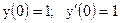
|
3.4. а) 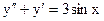 б)
б) 
| 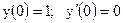
|
3.5. а)  б)
б) 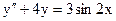
| 
|
3.6. а)  б)
б) 
| 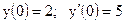
|
3.7. а)  б)
б) 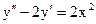
| 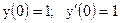
|
3.8. а) 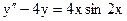 б)
б) 
| 
|
3.9. а) 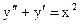 б)
б) 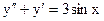
| 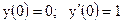
|
3.10. а) 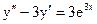 б)
б) 
| 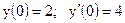
|
3.11. а)  б)
б) 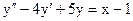
| 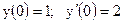
|
3.12. а)  б)
б) 
| 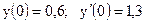
|
3.13. а)  б)
б) 
| 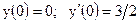
|
3.14. а) 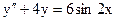 б)
б) 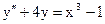
| 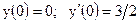
|
3.15. а) 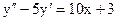 б)
б) 
| 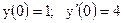
|
3.16. а)  б)
б) 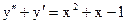
| 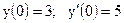
|
3.17. а) 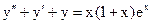 б)
б) 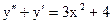
| 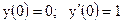
|
3.18. а) 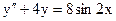 б)
б) 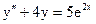
| 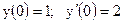
|
3.19. а) 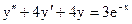 б)
б) 
| 
|
3.20. а) 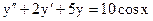 б)
б) 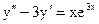
| 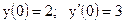
|
3.21. а) 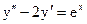 б)
б) 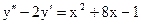
| 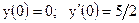
|
3.22. а) 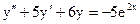 б)
б) 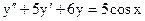
| 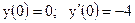
|
3.23. а) 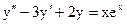 б)
б) 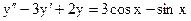
| 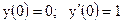
|
3.24. а) 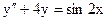 б)
б) 
| 
|
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 707; Нарушение авторских прав?; Мы поможем в написании вашей работы!