
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
С постоянными коэффициентами
|
|
|
|
Уравнение с разделяющимися переменными
Дифференциальные уравнения
Определение. Дифференциальным уравнением называется соотношение, связывающее независимую переменную, искомую функцию и её производные или её дифференциалы. В случае, когда неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, дифференциальное уравнение называется обыкновенным.
Рассмотрим некоторые типы дифференциальных уравнений.
у' = f 1(x)× f 2(y).
Решение.
dy/dx = f 1(x)× f 2(y) |× dx / f 2(y), f 2(y) ≠ 0,
dy/ f 2(y) = f 1(x)× dx,
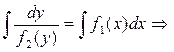 общее решение (общий интеграл) уравнения.
общее решение (общий интеграл) уравнения.
Случай f 2(y) = 0 рассматривается с помощью подстановки в исходное уравнение.
Пример 2.15. Решить уравнение 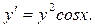
Решение.
dy/dx = у 2 сosx |× dx / у 2, у ≠ 0,
dy / у 2 = cosxdx,
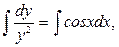
–1/ y = sinx + C,
y = –1/(sinx + C) – общее решение.
Рассмотрим случай у = 0.
Подставляя в исходное уравнение у = 0, получаем:
0' = 02 cosx, 0 = 0 – верно Þ у = 0 – решение уравнения.
Это решение не может быть получено как частное решение общего решения ни при каком значении С.
Ответ: y = –1/(sinx + C), у = 0.
2.81. Решить уравнения:
1) 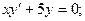 2)
2)  3)
3) 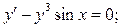
4)  5)
5)  6)
6) 
7)  8)
8) 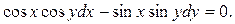
2. Однородные уравнения 1-го порядка
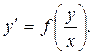
Уравнения решают с помощью замены
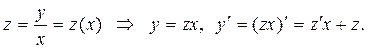
После подстановки z и 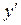 в исходное уравнение получается уравнение с разделяющимися переменными (см. п. 1).
в исходное уравнение получается уравнение с разделяющимися переменными (см. п. 1).
2.82. Решить уравнения:
1) 2)
2)  3)
3) 
4)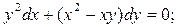 5)
5) 
6)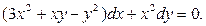
3. Линейные уравнения 1-го порядка
у ' + p (x)× y = f (x),
где p (x), f (x) – непрерывные функции
Пример 2.16. Решить уравнение у ' + xy = x.
Решение.
Пусть  тогда
тогда  и уравнение принимает вид
и уравнение принимает вид 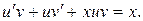
Группируя первое и третье слагаемые, получаем
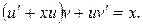
Равенство будет верным, если 
Найдем частное решение первого уравнения системы:
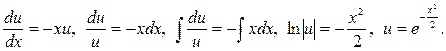
Подставим полученное решение во второе уравнение системы и найдем его общее решение:
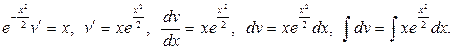
C помощью замены  получаем общее решение:
получаем общее решение: 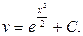
Подставляя найденные решения 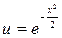 и
и  в равенство
в равенство  получаем решение исходного уравнения:
получаем решение исходного уравнения:

Ответ: 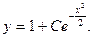
Задача Коши для уравнения 1-го порядка имеет вид
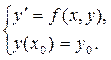
Пример 2. 17.
Решить задачу Коши 
Решение.
Найдем общее решение уравнения  :
:
dy / dx = х 2 у |× dx/у, у ≠ 0,
dy / у = x 2 dx,
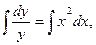
ln| y | = х 3 /3 + С.
Подставим в это решение х = 2 и у = 1 (см. условие у (2) = 1):
ln|1| = 23 /3 + С,
0 = 8/3 + С Þ С = – 8/3.
Подставляя это значение в общее решение, получаем
Ответ: ln|y| = (х3 – 8)/3.
2.83. Решить уравнение или задачу Коши:
1)  2)
2) 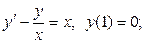
3)  4)
4) 
5) 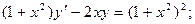 6)
6) 
7) 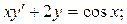 8)
8) 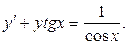
4. Линейные однородные уравнения 2-го порядка
 ,
,
где p, q  R.
R.
Решение.
Составим характеристическое уравнение  и решим его.
и решим его.
Возможны три случая:
1) k 1,2 R, k 1 ≠ k 2 (дискриминант D > 0);
R, k 1 ≠ k 2 (дискриминант D > 0);
2) k 1 ,2  R, k 1 = k 2 = k (D = 0);
R, k 1 = k 2 = k (D = 0);
3) k 1,2 = 
 C (D < 0).
C (D < 0).
Каждому из этих случаев соответствует общее решение уравнения:
1) 
2) 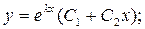
3) 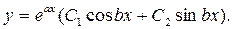
Пример 2. 18.
Решить уравнения:
1) 
2) 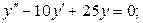
3) 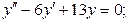
4) 
Решение.
1) 
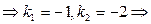 Ответ:
Ответ: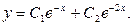
2) 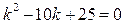
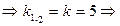 Ответ:
Ответ:
3) 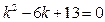
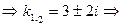 Ответ:
Ответ: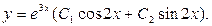
4) 
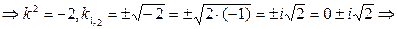
Ответ: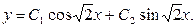
2.84. Решить уравнения:
1)  2)
2)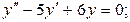 3)
3) 
4) 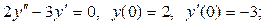 5)
5) 
6)  7)
7)  8)
8) 
5. Уравнения вида y(n) = f (x)
Решение.

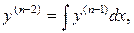 …,
…, 
Пример 2. 19.
Решить уравнение: 1. 2.
2. 
Решение.
1. 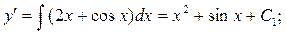
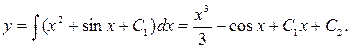
Ответ: 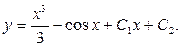
2. 

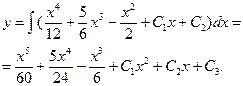
Ответ: 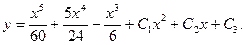
2.85. Установить вид частного решения неоднородного уравнения 2-го порядка с постоянными коэффициентами, если:
1)  2)
2) 
3) 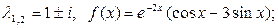
4) 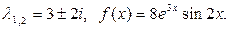
2.86. Решить уравнение или задачу Коши:
1)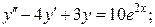 2)
2)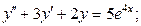
3)
4)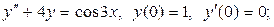
5)
6)
2.9. Последовательности и ряды
Определение. Числовой последовательностью называется функция натурального аргумента
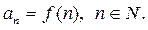
Пример 2.20.
Найти первые три члена последовательности 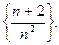
Решение.
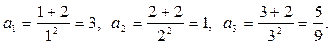
2.87. Найти пять первых членов последовательности 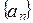 , если:
, если:
1) 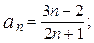 2)
2)  3)
3) 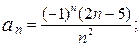 4)
4) 


2.9.1. Предел последовательности
Определение. Число А называется пределом последовательности 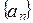 , если для любого сколь угодно малого числа ε > 0 найдется такой номер N = N (ε), что для всех n ≥ N будет выполняться неравенство ǀ аn − A ǀ < ε.
, если для любого сколь угодно малого числа ε > 0 найдется такой номер N = N (ε), что для всех n ≥ N будет выполняться неравенство ǀ аn − A ǀ < ε.
Пример. Доказать, используя определение предела последовательности, что предел последовательности  равен нулю.
равен нулю.
Решение.
Пусть ε > 0. Составим неравенство 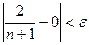 и решим его относительно n. Получаем:
и решим его относительно n. Получаем:

Итак, для любого ε > 0 существует такой номер 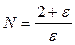 (или целой части дроби), что для всех
(или целой части дроби), что для всех 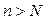 выполняется неравенство
выполняется неравенство 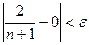 , т. е. предел последовательности
, т. е. предел последовательности  равен нулю. Например, при ε = 0,1 N = 21.
равен нулю. Например, при ε = 0,1 N = 21.
2.88. Доказать, используя определение предела последовательности, что 
 ;
; 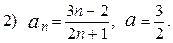
Пример 2.21. Найти предел последовательности 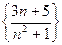 .
.
Решение.

2.89. Найти предел последовательности:
1)  2)
2) 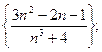 3)
3)  4)
4) 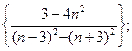
5)  6)
6)  7)
7)  8)
8) 
2.90. Вычислить пределы, используя равенство 

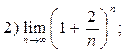
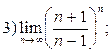
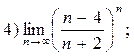

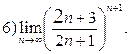
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 441; Нарушение авторских прав?; Мы поможем в написании вашей работы!