
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры выполнения заданий. Для студентов 3 курса экономического факультета
|
|
|
|
МЕТОДЫ И МОДЕЛИ
ПРАКТИЧЕСКОЕ ПОСОБИЕ
Для студентов 3 курса экономического факультета
Гомель 2006
Содержание
Введение
Содержание дисциплины
1. Теоретические основы метода моделирования
2. Методы решения задач оптимального планирования деятельности предприятия
Тема 1 Графический метод решения задач оптимального планирования
Тема 2 Решение задач оптимального планирования симплекс-методом
3. Модели исследования операций
Тема 1 Игровые методы и модели их использования
Тема 2 Сетевые модели
Задания:
1. Полосы листового проката длиной 200 см необходимо разрезать на заготовки трех типов: А, Б и В длиной соответственно 57, 82 и 101 см для производства 50 изделий. На каждое изделие нужно по 4 заготовки типов А и Б и 5 заготовок типа В.
Определить, какое количество полос проката необходимо разрезать тем или иным способом для получения требуемого количества изделий, чтобы отходы от раскроя были наименьшими.
Решение. Рассмотрим возможные способы раскроя одной ‚полосы на заготовки заданных типов. Для составления целевой функции, выражающей суммарную величину отходов, подсчитаем величины отходов при раскрое одной полосы по каждому из способов. При первом способе отходы от каждой полосы составят 200 — 57 х 3 = 29 (см), при втором способе 200 - (57 х 2 + 82) = 4 (см) и т.д. Полученные результаты сведем в таблицу 2.
Таблица 2 — Способы раскроя

Для производства 50 изделий необходимо 4 х 50 = 200 заготовок типа А, 4 х 50 = 200 заготовок типа Б и 5 х 50 = 250 заготовок типа В.
Введем следующие обозначения:
j — индекс способа раскроя;
i — индекс типа заготовки;
хj — количество полос, раскраиваемых j-м способом,
 ;
;
aij — количество заготовок i-го типа, получаемое при j-м способе раскроя,  ;
;
Сj — отходы при раскрое одной полосы j-м способом раскроя;
Bi — требуемое количество заготовок i-го типа.
В принятых обозначениях целевая функция задачи, выражающая минимум суммарной величины отходов при всех способах раскроя, будет иметь вид:
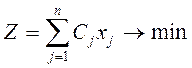
Ограничения задачи, показывающие общее количество заготовок каждого типа, которое необходимо получить при раскрое, будут иметь вид:
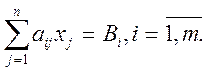
Обязательным является ограничение на неотрицательное значение количества раскраиваемых каждым способом исходных полос листового проката:
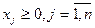
Если раскрыть знаки сумм и проставить значения индексов, то математическая модель задачи будет иметь вид:
Z = С1х1+С2х2+С3х3+С4х4+ С5х5 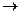 min
min
при ограничениях
а11 х1 + а12 х2 + а13 х3 + а14 х + а15 x5 = В1,
а21 х1 + а22 х2 + а23 х3 + а24 х4 + а25 x5 = В2,
а31 х1 + а32 х2 + а33 х3 + а34 х4 + а35 x5 = В3,
х1 >= 0, х2 >= 0, х3 >= 0, х4 >= 0, х5 >= 0.
Подставив численные значения используемых величин, получим следующую математическую модель задачи:
Z=29x1,+4x2+42x3+36х4+ 17х5 à min
при ограничениях:
3х1 + 2х2 + х3 = 200,
x2+ 2х4 + х5 = 200,
х3 + х5 = 250,
х1 >= 0, х2 > =0, х3 >= 0, x4 >= 0, х5 >= 0.
Решив задачу симплекс-методом, получим следующее оптимальное решение: х1 =0, х2 = 50, х3 = 100, х4 = 0, x5 = 150, Z = 6950 (ем). То же значение целевой функции получается и при другом плане раскроя: х1 = 50, х2 = 0, х3 = 50, х.4 = 0, x5 =200.
2. Составить оптимальный суточный рацион кормления на стойловый период для дойных коров живой массой 500 кг и суточным удоем 32 кг. На одну голову в сутки требуется не менее 22 кг кормовых единиц и 2502 г перевариваемого протеина. Рацион составляется из трех видов кормов: комбикорма, сена и силоса.
Содержание питательных веществ в единице каждого вида корма и себестоимость кормов показаны в таблице 3.
Согласно физиологическим особенностям животных в рационе должно содержаться не менее 30% концентратов и не более 25% грубых кормов от общей потребности в кормовых единицах.
Критерием оптимальности считается минимум себестоимости рациона.
Таблица 3 — Исходные данные
| Показатели | Содержание питательных веществ на 1 кг корма | ||
| комбикорм | сено | силос | |
| Кормовые единицы, кг | 0,5 | 0,2 | |
| Перевариваемый протеин; г | |||
| Себестоимость 1кг корма, усл. ден. ед. |
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 3869; Нарушение авторских прав?; Мы поможем в написании вашей работы!