Примеры выполнения заданий

Задания:

1 Построить модель производственной задачи, использующей две технологии и три вида ресурсов при значениях величин a_ij, b_i, и b_j,. заданных таблицей 30.

Таблица 30 — Исходные данные

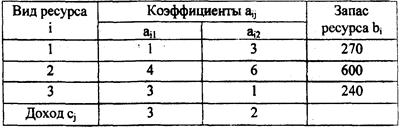
Решить задачу графически.

Решение. Математическая модель задачи в численном виде может быть записана следующим образом:

mах Z: 3х₁ + 2х₂, при ограничениях

х₁ + 3х₂ <= 270,

4x₁ + 6х₂ <= 600,

3x₁ + х₂ <= 240,

x₁ >= 0, x₂ >= 0.

Для построения допустимой области решений, заданной ограничениями - неравенствами, построим на плоскости многоугольник, ограниченный прямыми х₁ + 3х₂ = 270, 4x₁ + 6х₂ = 600, 3x₁ + х₂ = 240 (линии 1, 2 и 3 на рисунке 1) и координатными

осями x₁ = 0, x₂ = 0. Убедимся, что любая точка, лежащая внутри или на границе заштрихованной области, удовлетворяет всем исходным неравенствам системы, подставляя любую из точек заштрихованной области, например, начало координат (0; 0) в каждое

из неравенств системы.

Рисунок 1 — Решение

a) х₁ + 3х₂ = 270, b) 4x₁ + 6х₂ = 600 c) 3x₁ + х₂ = 240

x₁=90, x₂=60, x₁=0, x₂=100, x₁=0, x₂=240,

x₁=0, x₂=90, x₁=150, x₂=0, x₁=80, x₂=0.

Приравняем правую часть уравнения целевой функции некоторой постоянной величине Z = 90 и построим уравнение прямой 3x₁ + 2х₂ = 90 (х₁ = 0, х₂ = 45; х₂ = 0, х₁ = 30). Увеличивая Z, будем передвигать эту прямую параллельно самой себе в направлении вектора V = (с₁;с₂)= (3; 2), координатами которого являются коэффициенты при неизвестных уравнения прямой Z. Он перпендикулярен этой прямой и указывает направление возрастания Z. Максимальное значение Z = 300 достигается в точке С с координатами (60; 60), которая является точкой пересечения прямых 4x₁ + 6х₂ = 600, и 3x₁ + х₂ = 240.

2 Найти оптимальное сочетание посевов пшеницы и кукурузы на участках различного плодородия площадью 100 и 200 га.

Данные приведены в таблице 31.

Таблица 31 — Исходные данные

По плану должно быть собрано не менее 1500 ц. пшеницы и 4500 ц. кукурузы. Цена 1 ц. пшеницы 6 денежных единиц, кукурузы - 4 денежных единицы. Критерием оптимальности считается максимум валовой продукции в денежном выражении.

Решение Если обозначить через х₁ — площадь, отводимую под посев пшеницы на 1 участке, через х₂ — на 2, через х₃ и х₄ площади, отводимые под посев кукурузы соответственно на 1 и 2 участках, то ограничения задачи запишутся следующим образом:

x₁ + х₃ = 100,

х₂ + х₄ = 200,

20х₁ + 15х₂ >= 1500 (ограничение на сбор пшеницы),

35 х₃ +30х₄ >= 4500 (ограничение на сбор кукурузы),

х _j>= 0 (j= 1,4).

Стоимость пшеницы, которую предполагается собрать с двух участков, составляет 6 (20х₁ + 15х₂) денежных единиц; стоимость кукурузы - 4 (35 х₃ +30х₄) денежных единиц, а общая стоимость валовой продукции выразится суммой Z= 120х₁ + 90х₂ + 140х₃ + 120х₄, которая должна стремиться к максимуму

Для решения задачи графическим способом преобразуем составленную модель в каноническую форму введением дополнительных переменных х₅ >= 0 и х₆ >= 0:

Max Z = 120х₁ + 90х₂ + 140х₃ + 120х₄+ 0х₅ + 0х₆;

х₁ + х₃ = 100,

х₂ + x₄ =200,

20х₁ + 15х₂ – x₅ = 1500

35 х₃ +30х₄ – x₆ = 4500

х_j>0 (j= 1,6).

Выделим в системе ограничений какой-либо базис и убедимся, что число свободных переменных не превышает двух.

max Z; = 38000 - 20 х₁ - 30х₂,

x₃ = 100- х₁, = 200 - х₂,

x₅ = -1500+20х₁ +15 x₂,

х₆ = 4500-35х₁ -30х₂.

Перейдем к эквивалентной системе неравенств, опуская базисные переменные х₄, х₅ и х₆:

max Z = -20 х₁ - 30 х₂ + 38000,

x₁< =100,

х₂ <= 200,

20х₁+ 15х₂ >= 1500,

35х₁ +30х₁ <=4500,

x₁>= 0, х₂ >= 0.

Решение полученной двумерной задачи приведено на рисунке 2.

Рисунок 2 — Решение

При этом на каждой граничной прямой одна из переменных исходной задачи обращается в нуль. Так, неравенству 20 х₁+ 15х₂ >= 1500 соответствует граничная прямая АВ с уравнением 20х₁ + 15х₂ = 1500.

Но указанное неравенство образовано из третьего уравнения системы ограничений х₅ =- - 1500 + 20х₁ + 15х₂ путем отбрасывания переменной х₅, следовательно, на прямой АВ х₅ =0.

20х₁+15х₂= 1500; 35х+30x = 4500;

x₁ = 0, х₂ = 100, х₁ = 0, х₂ = 150,

х₂ = 0, х₁ = 75, х₂=0, х₁ = 128,75.

Из рисунка 2 видно, что наибольшего значения функция Z достигает в т. А пересечения прямых АВ и АЕ (х₂ = 0), имеющей координаты (75; 0), т.е. х₁ = 75, х₂ = 0. Одновременно в этой вершине х₅ = 0.

Значения других переменных, приводящих к оптимальному решению, находятся из системы ограничений с выделенным базисом:

х₃ = 100—75=25, х₄=200, х₆ = 2375, при этом Z =36500.

Таким образом, пшеницу следует посеять только на первом участке и засеять ею площадь в 75 га; кукурузу надо посеять на обоих участках, причем на первом - 25, а на втором – 200 га. Тогда валовая продукция достигнет (в денежном выражении) максимума и составит 36500 денежных единиц.

Дополнительные переменные х₅ и х₆, которые в канонической записи задачи соответственно равны х₅ = (20 х₁ + 15 х₂) - 1500 и х₆ = (35 х₁ + 30 х₂) - 4500, имеют вполне определенный экономический смысл: это превышение сбора пшеницы и кукурузы над плановым заданием. При найденном оптимальном сочетании посевов задание по сбору пшеницы будет выполнено (х₅ = 0), а по кукурузе перевыполнено на 2375 ц. (х₆ = 2375).

Задания:

1 Решить графическим методом задачу 1 первого задания.

2 Решить графическим методом задачу 2 первого задания.

3 Решить графическим методом задачу 3 первого задания.

4 Решить графическим методом задачу 4 первого задания.

5 Решить графическим методом задачу 5 первого задания.

6 Решить графическим методом задачу 6 первого задания.

7 Решить графическим методом задачу 7 первого задания.

8 Решить графическим методом задачу 9 первого задания.

9 Решить графическим методом задачу 29 первого задания.

10 Решить графическим методом задачу 35 первого задания.

Решить графическим методом следующие задачи линейного программирования при целевой функции: mах Z = х₁ + 2х₂.

1 - x₁ + x₂ < = 2,

5х₁+2х₂<=10,

5х₁-2х₂<=5,

х₁>= 0, х₂ >= 0.

2 - x₁ + 2x₂ < = 4,

3х₁+х₂ >= 3,

4х₁-3х₂ <=12,

х₁>= 0, х₂ >= 0.

3 x₁ + 2x₂ > = 2,

2х₁+х₂<=8,

4х₁-3х₂<=12,

х₁>= 0, х₂ >= 0.

4 - x₁ + 2x₂ < = 4,

2х_1-х₂<=6,

3х₁+х₂<=24,

х₁>= 0, х₂ >= 0.

5 3x₁ - x₂ > = 3,

-2х₁+3х₂<=12,

2х₁-х₂<=8,

х₁+4х₂>=8,

х₁>= 0, х₂ >= 0.

6 3x₁ - x₂ > = 1,

-х₁+3х₂<=13,

2х₁-х₂<=9

х₁+4х₂>=9,

х₁>= 0, х₂ >= 0.

Решить графическим методом следующие задачи линейного программирования:

7 mах Z =4 х₁ + 2х₂.

2х₁+3х₂<=18,

-х₁+3х₂<=9,

2х₁ - х₂<=10,

х₁>= 0, х₂ >= 0.

8 mах Z = х₁ + 2х₂.

3х₁+2х₂<=11,

-2х₁+х₂<=2,

х₁ - 3х₂<=0,

х₁>= 0, х₂ >= 0.

9 mах Z = 2х₁ + 8х₂.

х₁ - х₂<=1,

2х₁+х₂<=2,

х₁ - х₂>=0,

х₁>= 0, х₂ >= 0.

10 mах Z = 2х₁ + 3х₂.

3х₁+2х₂>=6,

х₁+4х₂>=4,

х₁>= 0, х₂ >= 0.

11 mах Z = 2х₁ + 4х₂.

3х₁+2х₂<=11,

-2х₁+х₂<=2,

х₁ - 3х₂<=0,

х₁>= 0, х₂ >= 0.

12 mах Z = х₁ - 2х₂.

х₁ - 2х₂ <=1,

х₁+х₂ >=2,

х₁ - ₂х₂<=0,

х₁>= 0, х₂ >= 0.

13 mах Z = 2х₁ + 4х₂.

4х₁+3х₂<=40,

12х₁+3х₂<=24,

х₁ <= 3, х₂ <=3,

х₁>= 0, х₂ >= 0.

14 mах Z = х₁ + х₂.

х₁+2х₂<=10,

х₁+2х₂>=2,

2х₁ + х₂<=10,

х₁>= 0, х₂ >= 0.

15 mах Z = 3х₁ + 2х₂.

х₁+х₂ >=1,

-5х₁+х₂<=0,

5х₁ - х₂ >=0,

х₁ -х₂ >= - 1,

х₁+х₂ <=6,

х₁>= 0, х₂ >= 0.

Дата добавления: 2014-10-15