Примеры выполнения заданий. 1 Решить задачу симплекс-методом, т.е

Задания:

1 Решить задачу симплекс-методом, т.е. определить mах Z = 3х₁ + 2х₂.

х₁+3х₂<=270,

4х₁+6х₂<=600,

3х₁ + х₂<=240,

х₁>= 0, х₂ >= 0.

Решение. Введение дополнительных неотрицательных переменных х₁, х₂, х₃ приведем задачу к каноническому виду:

max Z = 3х₁ + 2х₂ + 0х₃ + 0х₄+ 0х₅;

х₁ +3х₂ + х₃ = 270,

4х₁ + 6х₂ + x₄ =600,

3х₁ + х₂ + x₅ = 240

х₁>= 0, х₂ >= 0, х₃>= 0, x₄>= 0, x₅ >= 0.

Дополнительные переменные х₃, х₄, х₅ являются базисными, а х₁,х₂ - свободными. Дополнительные переменные по своему экономическому смыслу представляют предполагаемый избыточный объем ресурсов соответственно первого, второго и третьего видов.

Занесем коэффициенты целевой функции и ограничений задачи в таблицу 32.

Таблица 32 — Допустимое базисное решение

Поскольку базисные переменные х₃, х₄, х₅ входят в целевую функцию с коэффициентами 0, естественно, что начальное базисное решение х₃ = 270, х₄ = 600, х₅ = 240 с нулевым значением целевой функции. Отрицательные значения Z₁ = -3, Z₂ = -2 свободных переменных в оценочной строке указывают, что данное базисное решение может быть улучшено.

Выполняя шаг 2 алгоритма устанавливаем, что наименьшее отрицательное значение в оценочной строке равное 3, находится в первом столбце таблицы 32, который, становится ключевым.

Для увеличения целевой функции надо ввести в базис свободную переменную х₁, и вывести из базиса одну из базисных переменных х₃, х₄, х₅. На шаге 3 находим отношение 270/1, 600/4, 250/3 элементов вектора b к положительным элементам ключевого столбца и по наименьшему из этих отношений выбираем ключевую строку и ключевой элемент а₃₁, = 3, взятый в рамку.

В соответствии с шагом 4 по формулам выполняем преобразование элементов таблицы, включая и оценочную строку Z. Этим заканчивается первая итерация симплекс-метода, в результате чего из базиса выведена переменная х₅ и введена переменная х₁.

Новое базисное решение х₃ =190, х₄ =280, х₅= 80, связанное со значением целевой функции Z = 240, и преобразованные элементы приведены в таблице 33.

Таблица 33 — Новое базисное решение

В этой таблице имеется единственный отрицательный элемент Z ₂ = -1

Выполняя вторую операцию с ключевым элементом а₂₂= 14/3, получаем таблицу 34, в которой все коэффициенты оценочной строки неотрицательны.

Таблица 34 — Оптимальное решение

Оптимальное решение (х₁, х₂, х₃) = (60, 60, 30), Z = 300 показывает, что при одинаковых объемах производства первого и второго изделий, равных 60 единиц будет получен доход в 300 денежных единиц. При этом первый ресурс имеется в избытке х₃=30 единиц, а второй и третий используются полностью х₄=х₅ =0.

2 Решить задачу:

max Z = 8х₁ + 2х₂ - 2х₃ - 5х₄ - 6х₅;

х₁ +х₂ - х₃ - x₄= 16,

4х₁ - 2х₂ + 2х₃ - x₅ =20,

х₁>= 0, х₂ >= 0, х₃>= 0, x₄>= 0, x₅ >= 0.

Решение. Система ограничений задачи не содержит базисных переменных, поэтому введем в уравнение искусственные переменные х₆, х₇, включив их в целевую функцию с коэффициентом - М, значение которого заранее не фиксируется. Получим следующую задачу:

max Z = 8х₁ + 2х₂ - 2х₃ - 5х₄ - 6х₅ – Мх₆ – Мх₇;

х₁ +х₂ - х₃ - x₄ + х₆ = 16,

4х₁ - 2х₂ + 2х₃ - x₅ + х₇ =20,

x_j >0, j=1,…,7,

решение которой приведено в таблице 35. Отметим, что после того, как искусственная переменная была выведена из базисных переменных, в силу выбора коэффициента - М она уже не может больше попасть в число базисных переменных, поэтому в последующих симплекс-таблицах столбец, соответствующий этой переменной, можно исключить.

Таблица 35 — Решение

Оптимальное решение задачи: х₁ = 26/3, х₂ =22/3, х₃ =х₄ =х₅ = х₆ = х₇ = 0, Z = 84.

3 Решить задачу:

min Z = х₁ + 2х₂.

2х₁+х₂>=3,

2х₁-7х₂<=1,

2х₁ + 3х₂>=6,

х₁>= 0, х₂ >= 0.

Решение. Перейдем к эквивалентной задаче максимизации.

Для этого поменяем знаки коэффициентов целевой функции умножим на -1 первое и третье неравенства и введем дополнительные переменные х₃, х₄, х₅. В результате получаем задачу:

max Z = -х₁ - 2х₂ + 0х₃ + 0х₄+ 0х₅,

-2х₁ -х₂ + х₃ = -3,

2х₁ - 7х₂ + х₄ =1,

-2х₁ -3х₂ + х₅ = -6,

x_j >=0, j=1,…,5.

В исходной симплекс - таблице все элементы оценочной строки отрицательны. В Соответствии с шагами 1, 2 двойственного симплекс - метода выбираем ключевую строку, соответствующую наименьшему отрицательному элементу -6 в столбце свободных членов и, выполняя шаг 4, находим отношения коэффициентов оценочной строки к отрицательным элементам, ключевой строки, равные 1/(-2) и 2/(-3).

Большее из этих чисел указывает ключевой элемент а₃₁ = -2. Выполнив требуемые преобразования, на следующей итерации по тем же правилам находим ключевой элемент

а₂₂ = -10. После двух итераций двойственного симплекс - метода получаем оптимальный план:

х = (9/4, 1/2, 2, 0, 0), Z _max = -13/4 (таблица 36).

Таблица 36 — Решение

Это дает решение исходной задачи в виде х = (9/4, 1/2), Z= 13/4.

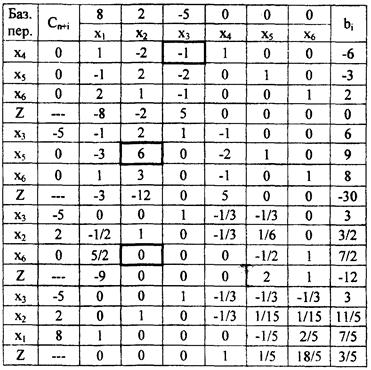
4 Решить задачу:

max Z = 8х₁ + 2х₂ - 5х₃,

-х₁ +2х₂ + х₃ >= 6,

х₁ - 2х₂ + 2х₃ > =3,

2х₁ + х₂ - х₃ < =2,

х₁>= 0, х₂ >= 0, х₃>= 0.

Решение. С помощью дополнительных переменных х_4, х₅, х₆ >= 0 переходим от ограничений неравенств к ограничениям - равенствам, и после умножения первого и второго ограничений на -1 окончательно получаем:

max Z = 8х₁ + 2х₂ - 5х₃,

х₁ -2х₂ - х₃ + x₄ = -6,

-х₁ + 2х₂ - 2х₃ + x₅ =-3,

2х₁ + х₂ - х₃ + x₆ =2,

x_j >=0, j=1,…,6.

Заполняем симплекс - таблицу и в соответствии с шагами 1и 2 двойственного алгоритма выбираем ключевую строку, соответствующую наименьшему отрицательному числу в столбце свободных членов. Сравниваем отношения (-6)/(-2) и (-6)/(-1) и поскольку второе из них большее, то ему соответствует ключевой столбец. Выполняя преобразования с ключевым элементом а₁₃ = -1, получаем эквивалентную задачу с неотрицательными значениями b_i. Проведя еще две итерации по правилам обычного симплекс - метода получаем оптимальный план: х = (7/5, 11/5, 3, 0, 0, 0), Z шах = 3/5 (таблица 37).

Таблица 37 — Решение

1 Решить симплекс-методом задачу 1 первого задания.

2 Решить симплекс-методом задачу 3 первого задания.

3 Решить симплекс-методом задачу 4 первого задания.

4 Решить симплекс-методом задачу 5 первого задания.

5 Решить симплекс-методом задачу б первого задания.

6 Решить симплекс-методом задачу 7 первого задания.

7 Решить симплекс-методом задачу 9 первого задания.

8 Решить симплекс-методом задачу 10 первого задания.

9 Решить симплекс-методом задачу 11 первого задания.

10 Решить симплекс-методом задачу 12 первого задания.

11 Решить симплекс-методом задачу 13 первого задания.

12 Решить симплекс-методом задачу 14 первого задания.

13 Решить симплекс-методом задачу 15 первого задания.

14 Решить симплекс-методом задачу 16 первого задания.

15 Решить симплекс-методом задачу 17 первого задания.

16 Решить симплекс-методом задачу 18 первого задания.

17 Решить симплекс-методом задачу 19 первого задания.

18 Решить симплекс-методом задачу 20 первого задания.

19 Решить симплекс-методом задачу 21 первого задания.

20 Решить симплекс-методом задачу 23 первого задания.

21 Решить симплекс-методом задачу 24 первого задания.

22 Решить симплекс-методом задачу 25 первого задания.

23 Решить симплекс-методом задачу 27 первого задания.

24 Решить симплекс-методом задачу 28 первого задания.

25 Решить симплекс-методом задачу 29 первого задания.

26 Решить симплекс-методом задачу 30 первого задания

27 Решить симплекс-методом задачу 31 первого задания

28 Решить симплекс-методом задачу 33 первого задания

29 Решить симплекс-методом задачу 34 первого задания

30 Решить симплекс-методом задачу 35 первого задания

Дата добавления: 2014-10-15