Показатели и критерии устойчивости и колеблемости развития финансовых процессов

В значительной части временных рядов эко­номических процессов между уровнями, особенно близко распо­ложенными, существует взаимосвязь. Ее удобно представить в виде коррелированной зависимости между рядом у₁, у₂,..., у_п и этим же рядом, но сдвинутым относительно первоначального по­ложения на τ моментов времени у_1+τ, у_2+τ,..., у_п+τ. Временное смещение τ называют сдвигом, а само явление – автокорреля­цией.

Автокорреляционная зависимость особенно существенна меж­ду последующими и предшествующими уровнями временного ряда. Поскольку классические методы математической статистики применимы лишь в случае независимости отдельных членов ряда между собой, то при анализе временных рядов чрезвычайно важ­но установить наличие и степень их автокорреляции. Для опре­деления уровня автокорреляции используется автокорреляцион­ная функция, состоящая из множества коэффициентов корреляции, вычисленных относительно исходного ряда и этого же ряда, сдви­нутого на τ моментов времени. Значение нормированной автокорреляционной функции вычисляется по формуле:

, (2.8)

где , .

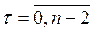Сдвиг, которому соответствует наибольший коэффициент ав­токорреляции, называется временным запаздыванием, или вре­менным лагом. Совокупность коэффициентов r₀, r₁, r₂,... назы­вают коррелограммом. Это же название используется для обозна­чения графика r_τ как функции от τ. Для удобства вычислений формулу (2.8) можно привести к следующему виду:

, (2.9)

где , .

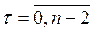Показатель, полученный по данной формуле, называют не­циклическим коэффициентом автокорреляции. Если временной ряд состоит из уровней, среднее значение которых равно нулю, то выражение (2.9) значительно упрощается:

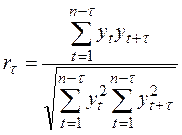
Для вычисления коэффициента автокорреляции при больших значениях n можно использовать упрощенную формулу:

В практиче­ских расчетах при построении коррелограмм количество членов автокорреляции r_τ ограничивают числом, содержащимся между n/4 и n/3.

Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру временного ряда. Если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка τ, то ряд содержит циклические колебания с периодичностью в τ моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, то можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию.

Частные коэффициенты автокорреляции измеряют связь между текущим значением переменной у₁, и предыдущими значениями этой переменной у_t-1, у_t-2,… у_t-k,,когда влияние всех промежуточных временных лагов устранено. Частный коэффициент автокорреляции первого порядка равен коэффициенту автокорреляции первого порядка. Частные коэффициенты автокорреляции второго и третьего порядка вычисляются соответственно по формулам:

, .

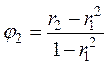Частные коэффициенты автокорреляции применяются при выборе модели авторегрессии.

Пример 1.8. Рассчитать коэффициенты автокорреляции для временного ряда «Денежная масса МО, млрд. руб.» (на начало месяца с января 1998 г. по декабрь 2000 г.). Построить график автокорреляционной функции.

Отметим, что во всех статистических пакетах существует возможность вычисления автокорреляционной функции. Для расчета коэффициента автокорреляции в Excel следует воспользоваться статистической функцией КОРРЕЛ, расчет коэффициента автокорреляции производится по формуле (2.9).

На рис.2.10 приведен график коэффициентов автокорреляции. Видим, что с ростом лага τ коррелограмма не стремится к нулю, такое поведение характерно для временного ряда, содержащего тренд.

Рис. 2.10. Коррелограмма ряда «Денежная масса»

Пример 1.9. На рис.2.11. приведен график коэффициентов автокорреляции для временного ряда «Выручка от реализации лакокрасочной продукции», содержащего сезонные колебания. Видим, что коррелограмма содержит периодические всплески, соответствующие периоду колебаний.

Рис. 2.11. Коррелограмма ряда «Выручка от реализации лакокрасочной продукции»

Разделение временного ряда на составляющие элементы (тренд, циклическая, сезонная и случайная составляющие) – условный прием. Устойчивость не означает обязательного повторения одинакового уровня из года в год, такое понимание устойчивости приравняло бы ее к застойному состоянию изучаемого явления. Слишком узким было бы понятие устойчивости временного ряда – как полного отсутствия в ряду всяких колебаний, так как полностью устранить влияние случайных факторов на показатель невозможно. Сокращение колебаний уровней ряда – одна из главных задач повышения устойчивости, но этим она не исчерпывается, необходимо определенное развитие явления. Отсюда следует, что устойчивость временного ряда понятие многоплановое.

Устойчивость временного ряда – это наличие необходимой тенденции изучаемого явления с минимальным влиянием на него неблагоприятных условий.

Из этого вытекают основные требования устойчивости:

§ минимизация колебаний уровней временного ряда;

§ наличие определенной, необходимой для общества тенденции изменения.

Устойчивость динамики развития экономического показателя, представленного временным рядом, можно рассматривать в двух аспектах: устойчивость развития относительно основной тенденции, т.е. линии тренда и устойчивость тенденции динамики самого тренда, т.е. его непрерывный рост или снижение.

Устойчивость уровней временного ряда определяется с помощью показателей: размах колеблемости средних уровней, индекс устойчивости уровней временных рядов, среднее линейное и среднее квадратическое отклонение, процентный размах, показателя скользящие средние, среднее процентное изменение, коэффициент колеблемости.

Под колебаниями уровней временного ряда следует понимать отклонения уровней от тренда, выражающего тенденцию изменения уровней. Термин «колеблемость» следует применять в указанном смысле только к временным рядам. Колебания – это процесс, протекающий во времени. В статистике, нередко «колеблемостью» называют пространственные различия уровня изучаемого признака, т.е. отожествляют колеблемость и вариацию. Необходимо четко разграничить эти термины: «вариация» - одновременное существование различающихся величин признака в совокупности и «колеблемость» - отклонения в разное время от тренда величины признака у одного и того же объекта.

Задача изучения колеблемости недооценивается. В учебниках по статистике, как правило, излагается методика измерения сезонных колебаний. Но это – лишь один из типов колебаний присущих экономическим, социальным и природным процессам.

Показатели, характеризующие колеблемость, не только имеют большое самостоятельное значение, но они используются в комплексном анализе временных рядов, совместно с показателями тенденции. Рассмотрим основные показатели, характеризующие силу колебаний: амплитуду, или размах колебаний; среднее линейное отклонение по модулю; среднее квадратическое отклонение.

Амплитуда или размах колебаний определяется как разность между наибольшим за период отклонением от тренда и наименьшим отклонением:

,

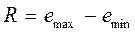где , 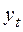- фактические уровни,- тренд.

Амплитуда зависит только от двух крайних величин отклонений и сильно подвержена влиянию случайностей. Чем длиннее временной ряд, тем больше вероятность того, что в нем встретится особенно большое отклонение от тренда. Поэтому с увеличением длины временного ряда возрастает в среднем и амплитуда колебаний. Имея самостоятельное значение в системе показателей колеблемости, амплитуда не может служить основной характеристикой колебаний.

Среднее линейное отклонение определяется по формуле:

.

Среднее линейное отклонение вполне пригодно как обобщающий показатель силы колебаний. Но известно, что модули величин из-за своих математических свойств широкого распространения в статистике не получили, в частности, с ними невозможно связать вероятностные законы распределения и нельзя использовать для прогнозирования доверительных границ возможных колебаний с заданной вероятностью. Поэтому основным абсолютным показателем колеблемости, как и вариации в пространстве, целесообразно считать среднее квадратическое отклонение от тренда:

,

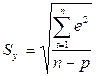где р – число параметров тренда, включая свободный член. Среднее квадратическое отклонение, как известно, входит в формулу нормального закона распределения вероятностей, на его основе можно рассчитывать вероятности ошибок прогнозов и их доверительные границы.

Относительные показатели колеблемости вычисляются делением абсолютных показателей колеблемости на средний уровень за весь изучаемый период. Наибольшее распространение среди относительных показателей колеблемости получил коэффициент колеблемости, который вычисляется как отношение среднеквадратического отклонения уровней ряда от линии тренда S_y к среднему значению уровней ряда: . Коэффициент колеблемости может быть выражен в %. При коэффициенте колеблемости меньше 10% колеблемость можно охарактеризовать как слабую, при - как умеренную, при - как сильную, при - как очень сильную.

Дополнить систему показателей колеблемости можно показателями устойчивости, как свойства, противоположного колеблемости. Коэффициентом устойчивости временного ряда называется величина:

,

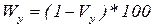т.е. дополнение коэффициента колеблемости до 1 или 100%. Чем ближе эта величина к 100, тем более устойчивым считается соответствующий временной ряд.

Пример 1.10. Методику вычисления показателей колеблемости рассмотрим на примере временного ряда, характеризующего деятельность коммерческого банка - объемы привлеченных средств.

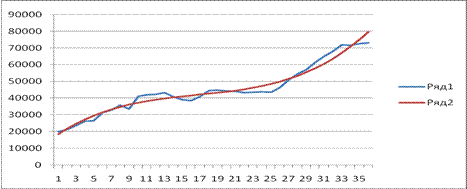
Рис. 2.12. Определение тренда временного ряда

(Ряд1- Объемы привлеченных средств банком; Ряд 2- сглаженный временной ряд).

Определив тренд временного ряда и вычислив по этому тренду значения для всего периода (рис.2.12), находим абсолютные отклонения фактических уровней от тренда, которые и служат исходной информацией к анализу колеблемости. Размах колебаний R=11392,7тыс.руб.; среднее линейное отклонение d=2303,876 тыс.руб.; среднее квадратическое отклонение S_y=2960,658тыс.руб.; коэффициент колеблемости V_y=6,6%. Коэффициент колеблемости меньше 10%, поэтому колеблемость можно охарактеризовать как слабую. Коэффициент устойчивости W_y=93,4%. Интерпретация этого показателя такова: в среднем ввиду колеблемости обеспечивается лишь 93,4% объема привлеченных средств по тренду.

Приняв гипотезу, что закон распределения отклонений от тренда близок к нормальному, можно вычислить вероятность того, что с учетом колебаний уровень ряда динамики отклонится от тренда не более чем на заданное число средних квадратических отклонений. Вероятность события (объем привлеченных средств банком отклонится в любом месяце от тренда не более чем на 2S_y в ту или другую сторону) составляет F(2)=0,954. Следовательно, вероятность того, что не произойдет отрицательного отклонения более чем на 2S_y от тренда составляет .

2S_y составляют в абсолютном выражении 5921,315 тыс.руб. следовательно, с вероятностью 0,977 можно гарантировать, что объем привлеченных средств отклонится в любом месяце вниз от тренда не более чем на 5921,315 тыс.руб. Эту величину, т.е. можно назвать одним из показателей устойчивости: с большей надежностью устойчиво обеспечен объем привлеченных средств не ниже величины .

Практическое значение изучения колеблемости в том, что зная, как изменяется колеблемость, можно учесть ее изменение в будущем при прогнозировании экономического процесса, характер колеблемости может пролить свет на ее причины и помочь в управлении процессом. Задача изучения причин колебаний выходит за пределы статистического анализа и должна выполняться наукой, изучающей те явления и процессы, динамика которых отражена временным рядом.

Рис. 2.13. Пилообразная колеблемость Рис. 2.14. Циклическая колеблемость

Колебания уровней временного ряда могут иметь разную форму, разное распределение по времени, разную амплитуду и частоту. Первичных или «чистых», типов колебаний во временных рядах выделяют три:

- пилообразная или маятниковая колеблемость при которой знаки отклонений от тренда чередуются строго поочередно (рис.2.13);

- долгопериодическая или циклическая, при которой несколько уровней подряд отклоняются от тренда в одну ту же сторону, а затем несколько уровней – в противоположную т.д. (рис.2.14);

- случайно распределенная во времени, при которой равновероятна любая последовательность знаков и величин отклонений от тренда (рис.2.15).

Рис. 2.15. Случайно распределенная во времени колеблемость

Как правило, ни один из типов в чистом виде на практике не встречается, но обычно один из типов является преобладающим для определенного экономического процесса. Знание типа преобладающей колеблемости имеет большое практическое значение при прогнозировании процесса и помогают экономисту понять, какие последствия могут иметь колебания для его сферы деятельности и разработать мероприятия по уменьшению колебаний либо по преодолению их отрицательных последствий.

Разные типы колеблемости объясняются, как правило, совершенно разными причинами. Так, «пилообразная» колеблемость чаще всего объясняется автоколебательным причинным механизмом. Долгопериодическая колеблемость обычно связана с циклами внешних факторов (солнечная активность, смена времен года и.т.д.). Причиной случайной колеблемости служит наличие большого числа независимых или слабосвязанных между собой факторов, влияющий на изучаемый процесс.

Для исследования типа колеблемости предложен ряд методов. Так М. Кендэл предложил критерий «поворотных точек», или локальных экстремумов, в ряду отклонений от тренда. Им показано, что при случайном распределении во времени колебаний число локальных экстремумов в среднем равно: , при среднеквадратическом отклонении. При «пилообразной» колеблемости, число локальных экстремумов будет равно n-2, при долгопериодической колеблемости - равно удвоенному числу циклов, умещающихся на длине периода n, поскольку каждый цикл содержит два экстремума. Ряд, изображенный на рис. 2.12 имеет 12 поворотных точек. Фактическое число экстремумов не попадает в интервал 22,7±2,5; следовательно, гипотеза о случайно распределенной во времени колеблемости не может быть принята.

Второй метод определения типа колеблемости основан на анализе коэфиициентов автокорреляции в ряду отклонений от тренда. Уже по коэффициенту автокорреляции первого порядка можно судить о преобладающем типе колебаний. При пилообразной колеблемости будет получена существенная отрицательная величина коэффициента автокорреляции, при долгопериодической колеблемости коэффициент автокорреляции окажется существенно положительным. При случайно распределенной во времени колеблемости коэффициент окажется несущественно отличным от нуля. Значимость коэффициента автокорреляции проверяется по специальным таблицам. Для временного ряда «Объемы привлеченных средств банком» первый коэффициэнт автокорреляции равен 0,618, и говорит о наличии долговременных периодических колебаний. Гармонический анализ выявил в изучаемом ряде колебания с периодом 18 и 9 месяцев. Объяснение колебаний выявленной периодичности следует искать в депозитной политике банка.

Рассмотренные в данной главе приемы статистического анализа временных рядов дают возможность осуществить первый шаг в исследовании тенденций развития изучаемого процесса, поскольку на их основе можно определить некоторые обобщающие характеристики движения во времени, проверить наличие тенденции, выявить в общем виде тенденцию развития в прошлом. Соответствующие результаты имеют самостоятельное значение в рамках прогностического анализа. Однако эти же результаты могут быть использованы в качестве вспомогательных средств при более обобщенной характеристике динамики с помощью формализованного описания тенденций развития, что и будет рассмотрено в следующих главах.

Контрольные вопросы и задания

1. Дайте определение временного ряда.

2. Назовите основные признаки классификации временных рядов. Приведите примеры временных рядов различных видов.

3. Какие требования предъявляются к составлению временных рядов?

4. Какие струк­турообразующие элементы (компоненты) выделяют при моделировании экономических процессов? Дайте их характеристику.

5. Какая модель временного ряда называется аддитивной (мультипликативной)?

6. Какие графики используются для изображения временного ряда?

7. Какие процедуры выполняют в ходе предварительного анализа временного ряда?

8. Какие методы выявления аномальных уровней временного ряда существуют?

9. С помощью каких методов определяется наличие тенденции во временном ряду?

10. Поясните сущность методов сглаживания.

11. На какие группы делятся методы сглаживания?

12. Перечислите основные шаги алгоритма сглаживания по простой скользящей средней.

13. Как проводится сглаживание временного ряда с периодическими колебаниями?

14. В чем состоит отличие алгоритма метода взвешенной скользящей средней от простой?

15. Сколько значений теряется при использовании скользящей средней с длиной интервала сглаживания m =7?

16. В чем состоит особенность метода экспоненциального сглаживания?

17. Объясните, как выбирается сглаживающий параметр α при реализации процедуры экспоненциального сглаживания.

18. С помощью каких статистических показателей описывается динамика экономических процессов?

19. Какая взаимосвязь существует между цепными и базисными коэффициентами роста?

20. Что такое автокорреляция уровней временного ряда?

21. Что такое автокорреляционная функция?

22. Что дает анализ автокорреляционной функции?

23. Дайте определение устойчивости временного ряда.

24. Какие показатели используются для характеристики колеблемости уровней временного ряда?

25. Как рассчитывается коэффициент устойчивости временного ряда?

26. Назовите основные типы колебаний во временных рядах.

27. В таблице приведены данные о выручке от реализации продукции предприятием, в тыс. руб.:

Период

Выручка от реализации продукции тыс.руб.

Определить наличие аномальных уровней методом Ирвина.

28. Для временного ряда, приведенного в задании 27, определить наличие тренда во временном ряду используя:

а) критерия серий, основанный на медиане;

б) критерий «восходящих» и «нисходящих» серий;

в) метод проверки разности средних уровней;

г) метод Фостера-Стьюарта.

29. Сгладить временной ряд, приведенный в задании 27, используя

а) пятичленную простую скользящую среднюю;

б) пятичленную взвешенную скользящую среднюю;

в) методом экспоненциального сглаживания, приняв сглаживающий параметр α=0,4.

Результаты сглаживания показать на рисунке.

30. В таблице приведены данные о доходах от операций с коммерческими кредитами, на начало месяца в тыс. руб.

Месяц

Доход от операций с кре-дитами, тыс.руб.

Определить средний уровень ряда, средний абсолютный прирост, средний темп роста и прироста.

31. Для временного ряда, приведенного в задании 30 рассчитать три первых коэффициента автокорреляции, сделайте вывод об их значимости. Построить график автокорреляционной функции.

Глава 3. Прогнозирование финансовых процессов с использованием кривых роста

Дата добавления: 2014-10-22