Методы оценки параметров кривых роста

Оценки параметров большинства кривых роста находятся с помощью метода наименьших квадратов (МНК). Суть МНК состоит в определении таких коэффициентов (параметров модели), при которых сумма квадратов отклонений фактических уровней ряда от соответствующих расчетных значений по кривой роста была бы наименьшей:

, (3.1)

где - фактическое значение уровня временного ряда;

- расчетное значение;

n – длина временного ряда.

При оценке параметров полиномиальных кривых

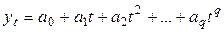
в результате минимизации выражения (3.1) получается система нормальных уравнений:

;

;

…………………………………………………….. (3.2)

;

.

Система (3.2) состоит из (q+1) линейных уравнений, содержащих в качестве известных величин и (q+1) неизвестных коэффициентов а_j. Решение этой системы относительно а₀, а₁, а₂,…, а_q позволяет вычислить искомые оценки параметров.

В матричном виде систему (3.2) можно записать в виде:

, (3.3)

где - вектор-столбец наблюдаемых значений уровней ряда,

- вектор столбец искомых параметров,

- матрица наблюдаемых значений объясняемых переменных.

Решив уравнение (3.3) получим оценки параметров полиномов, т.е.

.

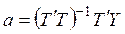Если полином имеет невысокую степень, системы для оценивания параметров выглядят намного проще. Нормальные уравнения для оценивания полинома первого порядка 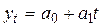имеют вид:

Решая систему двух линейных уравнений с двумя неизвестными, получим оценки параметров полинома первого порядка:

;

.

Преобразовав результат, получим следующие выражения для оценивания параметров:

,

.

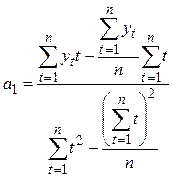Для оценивания параметров полинома второго порядка используют систему нормальных уравнений:

;

;

,

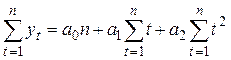для полинома третьей степени:

;

;

;

.

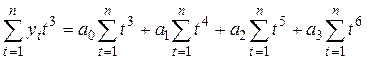При оценивании параметров экспоненциальной кривой 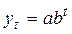, уравнение после логарифмирования приводят к линейному виду:

,

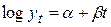где 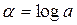и . МНК применяют к преобразованному уравнению и при оценке параметров исходят из критерия минимизации суммы квадратов отклонений в логарифмах:

.

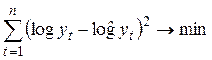Соответственно в нормальных уравнениях вместо фактических уровней временного ряда находятся их логарифмы. Для нахождения неизвестных параметров α и β необходимо решить систему уравнений:

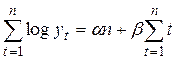
Найдя неизвестные параметры 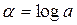и , значения a и b определим с помощью потенцирования и получим экспоненциальную функцию, аппроксимирующую временной ряд. Вследствие замены фактических значений уровней временного ряда их логарифмами полученные оценки оказываются смещенными, причем это смещение тем значительнее, чем больше разность между последовательными уровнями временного ряда.

При вычислении параметров модифицированной экспоненты, так же как и при вычислении параметров других кривых, имеющих асимптоту, следует различать два случая: во-первых, когда значение асимптоты известно или может быть определено заранее и, во-вторых, когда ее нужно вычислить на основании уровней изучаемого временного ряда вместе с другими параметрами кривой. Значение асимптоты можно определить заранее, исходя из свойств прогнозируемого процесса. Например, коэффициент использования оборудования не может превышать единицы или производственные мощности не позволяют наращивать объем производства выше определенного уровня, который и является оценкой асимптоты. В некоторых случаях значение асимптоты определяют экспертным путем.

Предположим, что значение асимптоты k известно, тогда определить другие параметры модифицированной экспоненты можно с помощью МНК, приведя преобразованное уравнение к линейному виду:

,

где k^* - заданное значение асимптоты. Прологарифмировав полученное выражение, получим

,

а затем, используя МНК, оценим параметры loga и logb.

Аналогично можно оценить параметры логистической кривой, если значение асимптоты k^* известно заранее. Уравнение логистической кривой преобразуем к виду:

.

Заменив k на известное значение k^* и прологарифмировав, получим линейное уравнение:

.

Используя МНК, оценим параметры lnb и a.

При оценке параметров кривой Гомперца при заданном значении асимптоты k^*, преобразуем уравнение кривой к виду:

.

Дважды прологарифмировав получим линейное уравнение, для оценки которого можно применить МНК:

;

Если значение асимптоты заранее неизвестно, то для нахождения параметров указанных выше кривых роста используются приближенные методы, в основе которых лежат другие критерии оптимальности. Рассмотрим некоторые из них.

Метод средних сумм основан на минимизации алгебраической суммы отклонений точек от аппроксимирующей кривой:

, (3.4)

где - ордината и абсцисса i -й точки ряда.

- параметры аппроксимирующей кривой.

Для нахождения параметров весь временной ряд разбивается равномерно на m групп (m<n) и для каждой из этих групп строят отношение вида (3.4) и приравнивают его к нулю. Таким образом, получается система из m алгебраических уравнений с m неизвестными, которая решается любым из методов линейной алгебры.

При определении параметров модифицированной экспоненциальной кривой можно использовать одну из модификаций метода средних, например, метод трех сумм. В этом случае уровни временного ряда разбиваются на три равные группы и суммируются. Обозначим каждую из таких сумм через и раскроем их, тогда:

,

где m - число уровней в группе (t=0,…m-1).

Так как , то

. (3.5)

Таким же образом определим выражение для двух других сумм:

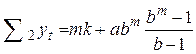; (3.6)

. (3.7)

Решая совместно уравнения (3.5-3.7), получим следующие выражения для параметров экспоненциальной кривой:

;

;

.

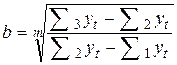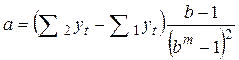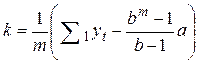Если в последнее выражение подставить найденные значения а и b, то k можно определить по формуле:

.

Обязательным условием использования метода трех сумм является предварительное сглаживание любым из известных способов.

Применим метод трех сумм для оценки параметров кривой Гомперца. С помощью логарифмирования кривую Гомперца легко представить в виде модифицированной экспоненты:

.

Используя рассмотренные выше приемы определения параметров модифицированной экспоненты, получим:

;

.

При оценке параметров логистической кривой вида 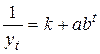в системе (3.5-3.7) значения надо заменить на . В результате после соответствующих преобразований получим:

;

;

,

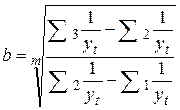или

.

Еще один метод, который используется для нахождения параметров S-образных кривых, если значение асимптоты заранее неизвестно - это метод трех точек.

Путь логистическая кривая имеет вид

. (3.8)

Подбор параметров по этому методу производится так, чтобы кривая прошла через некоторые заданные точки: уровни временного ряда в начале, в середине и в конце ряда, которые расположены на равном расстоянии друг от друга. На основании соотношения (3.8) получим:

;

;

,

где m - расстояние между точками.

Решив полученную систему уравнений, найдем значения параметров логистической кривой:

;

;

.

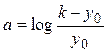Отметим, что обязательным условием использования метода трех точек так же как и метода трех сумм, является предварительное сглаживания временного ряда.

Параметры кривой Гомперца также можно определять с использованием метода трех точек. Кроме рассмотренных методов, для вычисления параметров S-образных кривых применяют специальные методы, основу которых составляет метод наименьших квадратов. Процедура реализации этих методов предполагает предварительное нахождение такого преобразования кривых роста, которое является линейным относительно параметров, и задача сводится к оценке параметров с помощью соответствующих регрессий.

Оценить параметры большинства кривых роста можно с помощью стандартных статистических пакетов. Как правило, в статистических пакетах предусмотрена возможность сохранения остатков для дальнейшего анализа. Построение линии тренда в программе Excel проводят с помощью средства Мастер диаграмм.

Пример. Используя средства программы Excel подобрать линию тренда для временного ряда «Денежная масса МО, млрд. руб.» (на начало месяца с января 1998 г. по декабрь 2000 г.), исходные данные представлены в примере 1.6 в параграфе 2.3.

Решение. Выделив данные, которые будут изображены на рисунке, построим график временного ряда, используя средства Мастер диаграмм (рис.3.11).

Рис. 3.11. Построение графика временного ряда с помощью Мастер диаграмм

Программа Excel предоставляет дополнительные возможности по работе с диаграммами, например, возможность создания линии тренда. С помощью Мастер диаграмм можно построить такие модели как линейные, полиномиальные, логарифмические, степенные и экспоненциальные. Для построения моделей необходимо щелкнуть правой кнопкой мыши на одном из рядов диаграммы. Из контекстного меню выбрать команду Добавить линию тренда (рис. 3.12).

Рис. 3.12. Результат работы Мастер диаграмм. Добавление линии тренда.

На экране появится диалоговое окно Линия тренда (рис.3.13). Далее нужно выбрать тип аппроксимирующей кривой. При выборе типа кривой Полиномиальная необходимо ввести значение степени. В случае необходимости можно ввести количество прогнозируемых периодов, отображение на диаграмме уравнения, величины достоверности аппроксимации (рис. 3.14).

Рис. 3.13. Результат работы Мастер диаграмм. Выбор аппроксимирующей кривой.

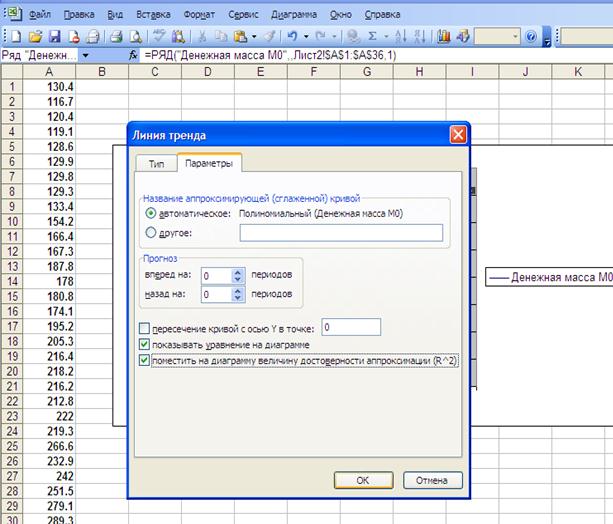
Рис. 3.14. Результат работы Мастер диаграмм. Установка параметров тренда с помощью вкладки Параметры.

На рис. 3.15. приведен результат построения тренда для временного ряда «Денежная масса». Аппроксимирующая кривая – полином второй степени:

.

Рис. 3.15. Построение тренда временного ряда «Денежная масса»

Контрольные вопросы и задания

1. Из каких предположений исходят при экстраполяция на основе кривых роста?

2. Перечислите этапы разработки прогноза с использованием кривых роста.

3. Охарактеризуйте основные типы кривых роста, применяемых для моделирования экономических процессов.

4. Назовите методы предварительного выбора кривых роста.

5. Какие предположения должны выполняться при предварительном выборе полиномиальной кривой методом конечных разностей(методом Тинтнера).

6. В чем суть метода конечных разностей(метода Тинтнера).

7. Перечислите основные этапы выбора кривой на основе метода характеристик прироста.

8. Какой метод используется для оценки параметров кривых роста?

9. В таблице приведены данные о ценах на сырье, руб.

Период

Цена, руб.

Выберите степень аппроксимирующего полинома методом конечных разностей.

10. По результатам выполнения задания 9 постройте полиномиальную модель. Расчеты выполните с использованием программных средств обработки данных.

Глава 4. Сезонные колебания в финансовых процессах

Дата добавления: 2014-10-22