Экспоненциальное сглаживание

Адаптивные модели базируются на двух схемах: скользящего среднего (MA -модели) и авторегрессии (АR -модели).

Согласно схеме скользящего среднего, оценкой текущего уровня является взвешенное среднее всех предшествующих уровней, причем веса при наблюдениях убывают по мере удаления от последнего уровня, т. е. информационная цен­ность наблюдений признается тем большей, чем ближе они к концу интервала наблюдений. Такие модели хорошо отра­жают изменения, происходящие в тенденции, но в чистом виде не позволяют отражать колебания.

Модель простой экспоненциальной средней описывается выражением:

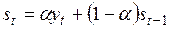, (5.1)

и используется, как отмечалось ранее, для сглаживания временных рядов. Для оценки ее текущего значения к величине экспоненциальной средней в момент времени (t-1), взятой с весом (1-α), необходимо добавить величину текущего фактического уровня ряда , умноженного на коэффициент α.

Рассмотрим процедуры прогнозирования, выполняемые с использованием моделей экспоненциальных средних. Экспоненциальное сглаживание, как указывалось в параграфе 2.3осуществляется по формуле:

,

здесь β=1-α, или

,

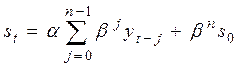где n – количество членов исходного ряда;

s₀ - величина, характеризующая начальные условия.

При n→∞ и β<1 коэффициент βⁿ→0, а сумма коэффициентов уровней ряда 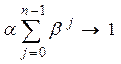, следовательно, в этом случае экспоненциальная средняя не зависит от начальных условий и полностью определяется суммой произведений уровней ряда на соответствующие им коэффициенты:

.

Таким образом, величина s_t оказывается взвешенной суммой всех членов ряда, причем веса падают экспоненциально в зависимости от дальности периода наблюдений. Например, если α=0,3, тогда вес текущего наблюдения равен 0,3; вес предыдущего наблюдения y_t-1 равен α ּ β=0,3 ּ 0,7=0,21; для наблюдения y_t-2 равен α ּ β²=0,3 ּ 0,7²=0,147 и т.д.

Пусть модель временного ряда имеет вид:

,

где а₁=const;

ε_t – случайные неавтокоррелированные отклонения нулевым математическим ожиданием и дисперсией σ ².

В работах Р.Брауна показано, что экспоненциальная средняя s_t имеет то же математическое ожидание, что и ряд y_t, но меньшую дисперсию:

;

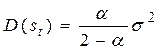. (5.2)

Так как , то дисперсия экспоненциальной средней 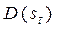меньше дисперсии временного ряда, равной 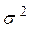. Из формулы (5.2) видно, что при высоком значении α дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда y_t. Чем меньше α, тем в большей степени уменьшается дисперсия экспоненциальной средней, таким образом, экспоненциальная средняя играет роль фильтра, поглощающего колебания исходного временного ряда.

Предположим, что модель временного ряда имеет вид:

,

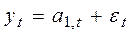где а_1,t - изменяющийся во времени средний уровень ряда;

ε_t – случайные неавтокоррелированные отклонения нулевым математическим ожиданием и дисперсией σ ².

Прогнозная модель в этом случае имеет вид:

,

где 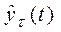- прогноз, сделанный в момент t на τ шагов вперед;

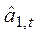- оценка а_1,t.

Экспоненциальная средняя служит средством оценки единственного параметра модели:

,

т.е. все свойства экспоненциальной средней распространяются на прогнозную модель. В выражении (5.3)

, (5.3)

полученному из (5.1), величина 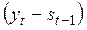есть погрешность прогноза, а новый прогноз s_t получается в результате корректировки предыдущего прогноза с учетом его ошибки. В этом и проявляется сущность адаптации этой модели.

Дата добавления: 2014-10-22