Адаптивные модели прогнозирования сезонных процессов

Рассмотрим адаптивные модели аддитивной и мультипликативной формы, имеющие явный механизм отображения сезонного развития исследуемого процесса.

Прогноз в момент времени t на τ шагов вперед по аддитивной модели Хольта-Уинтерса определяется выражением:

, (5.5)

,

,

,

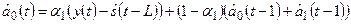где s - аддитивные сезонные коэффициенты,

L – период сезонности (для квартальных данных L=4, для месячных данных L=12).

Текущая оценка формируется на основе двух взвешенных в соответствии со значениями параметра сглаживания компонент – очищенного от сезонных колебаний фактического уровня и его значения в предыдущий период. При определении сезонных коэффициентов берется их последняя оценка, полученная для аналогичной фазы цикла, и новая оценка, учитывающая скорректированную величину среднего уровня.

Прогноз по мультипликативной модели Хольта-Уинтерса определяется выражением:

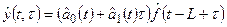, (5.6)

,

,

,

Где – мультипликативные сезонные коэффициенты.

Текущая оценка параметра формируется на основе взвешенной суммы текущей оценки , полученной путем исключения сезонных колебаний из ряда фактических значений, предыдущей оценки и оценки коэффициента роста , характеризующего изменение среднего уровня процесса за полный сезонный цикл в единицу времени. При определении сезонного коэффициента f учитывается скорректированная величина среднего уровня.

Начальные оценки параметров , , f могут быть получены различными способами. Например, начальная величина сезонных коэффициентов может определяться на основе данных первого года наблюдений, путем вычисления отношений каждого уровня ряда к среднегодовой величине. За начальное значение коэффициента можно взять среднюю величину наблюдений первого года, начальное значение коэффициента приравнивается нулю. Начальные значения параметров и можно определить и другими способами, например, построить уравнение регрессии по начальным наблюдениям ряда.

Практика показывает, что при относительном постоянстве амплитуды сезонной волны целесообразно использовать аддитивную модель, а при изменении сезонной волны в соответствии с тенденцией среднего уровня – мультипликативную.

П. Харрисон предложил метод, названный «волновым трендом» (seatrend) для корректировки сезонной компоненты в адаптивных моделях Уинтерса и Брауна. В данном методе для корректировки сезонной компоненты используется гармонический анализ. Сглаженные оценки для векторов сезонных коэффициентов получаются по формуле:

,

где 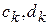- коэффициенты ряда Фурье,

знак означает суммирование только по статистически значимым гармоникам.

Начальные значения коэффициентов 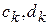определяются по формулам:

,

,

, ,

где - начальные оценки сезонных коэффициентов. Далее коэффициенты пересчитываются по следующим формулам:

,

,

где - ошибка в определении сезонного коэффициента в момент времени t. Величина e_t рассчитывается для аддитивной и мультипликативной модели по формулам:

,

,

где a_t – оценка уровня ряда в момент времени t без учета сезонной компоненты. В модели Харрисона, таким образом, обновление вектора сезонных коэффициентов происходит на каждом шаге.

Х. Тейл и С. Вейдж предложили для моделирования тренд-сезонных временных рядов использовать аддитивную модель вида:

,

,

,

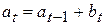где а_t – значение тренда ряда Y_t в момент t,

b_t – изменение тренда от момента (t-1) к моменту t,

s_t – сезонная компонента с периодом сезонности L,

e_t, v_t, q_t – случайные некоррелированные величины с нулевым средним значением, постоянной дисперсией и отсутствием автокорреляции.

Данный метод дает наилучшие результаты лишь при соответствии исследуемого процесса стохастическому процессу Тейла-Вейджа. Для рядов, описываемых процессами Тейла-Вейджа, автокорреляционная функция вторых разностей должна иметь следующие свойства:

,

,

при .

Возможно построение сезонных моделей путем комбинирования различных типов тенденций с коэффициентами аддитивного и мультипликативного вида. В зависимости от характера динамики моделируемого процесса в таблице (5.3) приведены девять моделей, объединенных в три группы.

Таблица 5.3

Вид моделируемого процесса

Тенденция Роста	Характер сезонного эффекта модели
Отсутствие сезонного эффекта	Аддитивный сезонный эффект	Мультипликативный сезонный эффект
Отсутствие тенденции роста
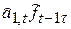
Аддитивный рост
Экспонен-циальный рост

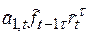
Следуя данному подходу, для любой из этих моделей оценка параметра осуществляется по формуле:

,

где a - параметр сглаживания (0<a<1), значения d₁ и d₂ принимают значения в соответствии с типом моделируемого процесса.

Итак, в адаптивных моделях происходит обновление сезонных колебаний на каждом шаге. Использование данных моделей для прогнозирования тренд-сезонных процессов позволит учесть неоднородность сезонных колебаний в различные кварталы (месяцы) и повысить точность прогноза.

Следует отметить, что мультипликативную модель можно преобразовать в аддитивную, если перейти к логарифмам:

, (5.7)

это дает возможность представить экономический процесс, содержащий сезонные колебания в виде различных комбинаций моделей двух типов.

Пример построения моделей Хольта-Уинтерса с аддитивными и мультипликативными коэффициентами сезонности приведен в параграфе 9.2.

Дата добавления: 2014-10-22