Полиномиальные адаптивные модели

Если тенденция исследуемого процесса близка к линейной, то для анализа и прогнозирования такого процесса используются модели линейного роста. Прогнозные оценки по таким моделям на τ шагов вперед получают по уравнению:

,

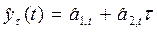где 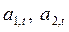- текущие оценки коэффициентов адаптивного полинома первого порядка, подлежащие определению.

В двухпараметрической модели Хольта оценка коэффициентов производится следующим образом:

;

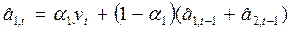, (5.4)

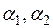- параметры экспоненциального сглаживания, называемые также параметрами адаптации, для которых должно выполняться условие .

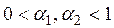Обозначим через ошибку прогноза, т.е. отклонение прогнозный оценки, полученной в момент (t-1), на один шаг вперед (τ=1) от фактического уровня ряда. Тогда уравнения (5.4) можно переписать в следующем виде:

;

.

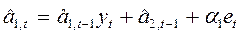Напомним, что через 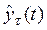обозначается прогноз, сделанный в момент t на τ шагов вперед, т.е. в данном случае через 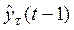обозначен прогноз, произведенный в момент (t-1) на один шаг вперед.

Частным случаем модели Хольта является модель линейного ряда Брауна:

;

,

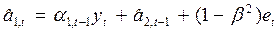Здесь β – параметр дисконтирования (0<β<1), характеризующий уменьшение веса данных наблюдения за единицу времени.

Введение дополнительного члена в модель, учитывающего разность ошибок прогнозирования, не привело к ее значительному улучшению, и она не получила широкого распространения.

Понятие экспоненциальной средней можно обобщить на случай экспоненциальных средних более высоких порядков. Выравнивание р -го порядка по формуле

,

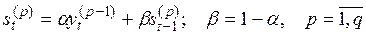является простым экспоненциальным сглаживанием, примененным к результатам сглаживания (р-1) -го порядка. В общем случае принимается гипотеза, что исследуемый процесс, состоящий из детерминированной и случайной компоненты, может быть описан полиномом q -го порядка, а прогноз на τ шагов вперед осуществляется по формуле

,

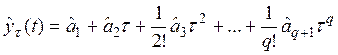где 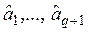- параметры, подлежащие определению.

В фундаментальной теореме метода экспоненциального сглаживания утверждается, что (q+1) неизвестных коэффициентов полинома q -го порядка могут быть оценены с помощью линейных комбинаций (q+1) значений 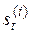, 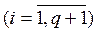. Следовательно, задача в данном случае сводится к вычислению значений функций сглаживания и через их линейные комбинации – к определению коэффициентов полинома.

В практических расчетах обычно используются полиномы не выше второго порядка. В таблице 5.1. приведены соответствующие формулы расчета по этим моделям.

Таблица 5.1.

Рекуррентные формулы для расчета параметров адаптивных полиномиальных моделей

Степень полино-миаль-ной модели	Экспоненциаль-ные средние	Начальные условия	Оценки коэффициентов	Прогнозная модель

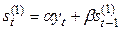
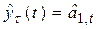
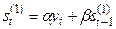
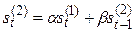
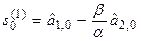
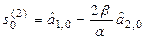
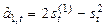
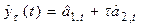
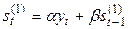
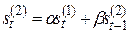
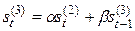
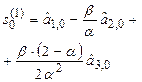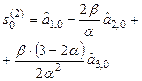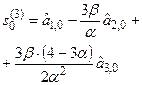
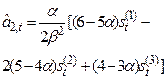
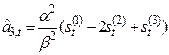
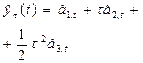
Процедура построения прогнозной модели методом экспоненциального сглаживания сравнительна проста. Определив одним из возможных способов параметр сглаживания α и начальные условия 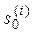по соответствующим формулам, приведенным в таблице 5.1., рассчитывают экспоненциальные средние 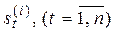, коэффициенты модели 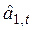и прогноз на τ шагов вперед. Ошибки прогнозов, вычисленные на каждом шаге процедуры, накапливаются для дальнейшей оценки точности прогноза. Окончательная прогнозная модель формируется на последнем шаге вычислений при t=n по последним значениям коэффициентов. Подставляя в нее заданное время упреждения прогноза τ, получают результат прогнозирования. При поступлении новой информации, приняв в качестве начальных условий последние значения функции сглаживания 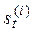можно продолжать дальнейшее сглаживание.

Необходимые для расчета начальные условия в случае отсутствия априорной информации о характере исследуемого процесса могут быть получены путем оценивания параметров кривой роста 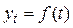, построенной по нескольким первым точкам ряда. Использование же в качестве начальных условий только первого уровня ряда нежелательно ввиду возможной его вариации, которая при малом объеме выборке может значительно исказить прогнозные расчеты.

Одним из наиболее сложных моментов использования метода экспоненциального сглаживания является выбор величины параметра сглаживания α. С одной стороны, повышение скорости реакции модели на резкое изменение процесса, увеличение веса более «свежих» наблюдений может быть достигнуто при выборе больших значений α. С другой стороны, стремление лучше сгладить случайные отклонений и обеспечить устойчивость модели к кратковременным разовым изменениям процесса диктует необходимость уменьшений α. Автор метода экспоненциального сглаживания Р. Браун предложил следующую формулу расчета α:

,

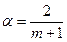где m – число уровней, входящих в интервал сглаживания. В качестве удовлетворительного практического компромисса он рекомендовал брать α в пределах от 0,01 до 0,3. Однако ряд исследований показал, что наилучшим параметром сглаживания может быть α>0,3. Следует отметить, что близость величины параметра сглаживания к единице является симптомом неправильного выбора структуры модели, хотя при краткосрочном прогнозировании выбор больших значений α, позволяющих учитывать ценность более «свежих» данных, вполне оправдана.

Поэтому величину m, как и непосредственно параметр α, лучше определять эмпирическим путем. Поиск оптимальных значений параметра сглаживания для адаптивных полиномиальных моделей может также осуществляться путем перебора его различных значений. В этом случае в качестве оптимального выбирается то значение α, при котором получена наименьшая дисперсия ошибки, вычисленная либо относительно всех сглаженных уровней динамического ряда, либо не использованных в расчетах уровней, специально оставленных для проверки качества прогнозных моделей.

Порядок адаптивной полиномиальной модели обычно определяется на основе визуального анализа графика процесса, качественного анализа, с помощью метода изменения разностей, а также сравнения статистических характеристик моделей на участке обучения и ретроспективного прогноза.

Пример. Построить адаптивную модель Хольта по имеющимся данным об объеме привлеченных средств (депозитах) в коммерческом банке.

1 год	Депозиты, в тыс.руб.	2 год	Депозиты, в тыс.руб.	3 год	Депозиты, в тыс.руб.
Январь		Январь		Январь
Февраль		Февраль		Февраль
Март		Март		Март
Апрель		Апрель		Апрель
Май		Май		Май
Июнь		Июнь		Июнь
Июль		Июль		Июль
Август		Август		Август
Сентябрь		Сентябрь		Сентябрь
Октябрь		Октябрь		Октябрь
Ноябрь		Ноябрь		Ноябрь
Декабрь		Декабрь		Декабрь

Параметры сглаживания возьмем равные .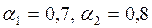

1. Начальные значения параметров 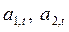при t=0 оценим по пяти первым точкам временного ряда с помощью метода наименьших квадратов. Расчеты удобно выполнить с помощью мастер-диаграмм ППП Excel. Для нахождения коэффициентов добавим линию тренда на графике временного ряда. Результаты линейной аппроксимации приведены на рис. 5.2.

Рис.5.2. Оценка линии регрессии методом наименьших квадратов

по пяти начальным точкам

Уравнение тренда имеет вид 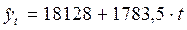, откуда начальные значения параметров модели, соответствующие моменту времени t=0:

.

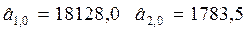2. Используя начальные оценки параметров 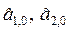, соответствующие параметру времени t=0, находим оценки коэффициентов на момент времени t=1:

;

;

, .

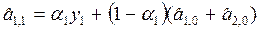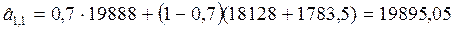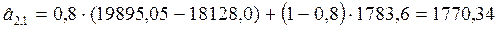3. Находим значение 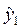для момента времени t= 1 по формуле:

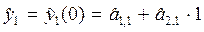
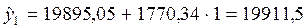
2. Корректируем параметры 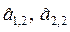для момента времени t=2:

3. ;

;

, .

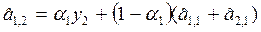6. Находим значение 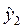для момента времени t=2 по формуле:

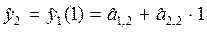
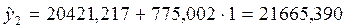
7. Далее возвращаемся к пункту 5 и повторяем вычисления до конца наблюдений.

Результаты расчетов приведены в таблице 5.2.

Таблица 5.2

Результаты расчета прогнозной модели Хольта при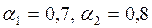

t
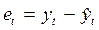
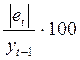
		18128.000	1783.500
		19895.050	1770.340	19911.500	-23.500	0.12
		20421.217	775.002	21665.390	-415.390	1.95
		21233.866	805.119	21196.219	2553.781	10.75
		23236.695	1763.288	22038.985	4108.015	15.71
		25802.895	2405.617	24999.983	1357.017	5.15
		26912.454	1368.770	28208.512	3047.488	9.75
		30363.567	3034.645	28281.224	4611.776	14.02
		33044.564	2751.726	33398.212	2226.788	6.25
		35676.387	2655.804	35796.290	-2442.290	7.32
		34847.457	-131.983	38332.191	2620.809	6.40
		39081.742	3361.031	34715.474	7156.526	17.09
		42043.232	3041.398	42442.774	-255.774	0.61
		43056.289	1418.725	45084.630	-1964.630	4.56
		43526.504	659.917	44475.014	-3692.014	9.05
		41804.026	-1245.999	44186.421	-5152.421	13.20
		39491.208	-2099.454	40558.028	-2101.028	5.46
		38137.426	-1502.917	37391.754	3571.246	8.72
		39664.453	921.038	36634.510	7739.490	17.44
		43237.447	3042.603	40585.491	4171.509	9.32
		45213.915	2189.695	46280.050	-1955.050	4.41
		45248.583	465.673	47403.610	-3465.610	7.89
		44470.877	-529.030	45714.256	-2395.256	5.53
		43505.854	-877.824	43941.847	-445.847	1.03
		43235.609	-391.761	42628.030	1050.970	2.41
		43428.454	75.924	42843.848	694.152	1.59
		43527.914	94.752	43504.379	2752.621	5.95
		45466.700	1569.979	43622.666	7090.334	13.98
		49610.104	3628.719	47036.679	7485.321	13.73
		54137.047	4347.298	53238.823	3824.177	6.70
		57489.404	3551.345	58484.345	2773.655	4.53
		61192.825	3673.006	61040.749	3953.251	6.08
		64955.549	3744.781	64865.830	3253.170	4.78
		68293.399	3419.236	68700.330	3170.670	4.41
		71823.491	3507.920	71712.635	-134.635	0.19
		72704.023	1406.010	75331.411	-2869.411	3.96
		72956.410	483.111	74110.034	-1039.034	1.42
				среднее	1412.802	6.99

На последнем шаге получили следующую прогнозную модель:

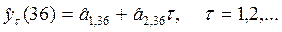
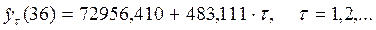
Точечный прогноз на шаг

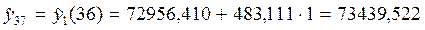
Точечный прогноз на шаг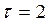

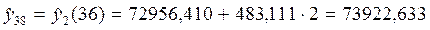
Точечный прогноз на шаг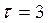

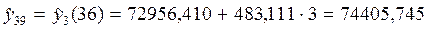
На рисунке 5.3 представлены графики исходного ряда, смоделированного ряда и точечный прогноз на три шага.

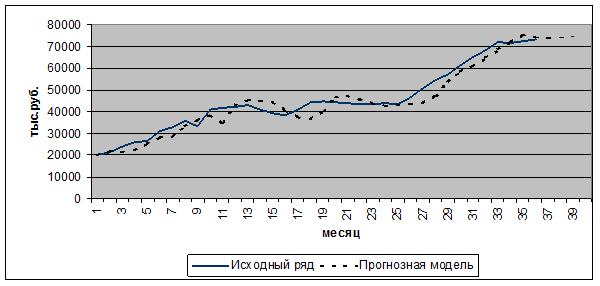
Рис. 5.3 Исходный ряд, смоделированный ряд и точечный прогноз

Дата добавления: 2014-10-22