
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление массы, статических моментов и моментов инерции тонких пластинок
|
|
|
|
| Чтобы вычислить механические характеристики тонких пластинок, занимающих область D Ì XOY, (массу, статические моменты, моменты инерции), нужно заметить, что все эти величины являются аддитивными, и применить общую методику приложений интегрального исчисления. | 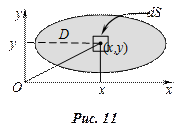
|
Сначала нужно вспомнить простейшие формулы из физики:
| 1) | 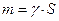
| - так вычислить массу  пластинки, площадь которой пластинки, площадь которой  , а поверхностная плотность материала , а поверхностная плотность материала 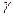 является постоянной величиной; является постоянной величиной;
|
| 2) | 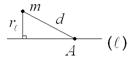
| если точечная масса  расположена на расстоянии расположена на расстоянии 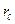 от оси от оси  , то её статический момент относительно оси , то её статический момент относительно оси  вычисляется по формуле вычисляется по формуле
 ; ;
|
при этом точки, расположенные по разные стороны от прямой  , имеют статические моменты разных знаков; , имеют статические моменты разных знаков;
| ||
| 3) | момент инерции точечной массы  относительно оси относительно оси  вычисляется по формуле вычисляется по формуле  , а относительно некоторой точки , а относительно некоторой точки  - по формуле - по формуле 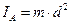 , где , где  - это расстояние от материальной точки до точки - это расстояние от материальной точки до точки  . .
|
Эти формулы нельзя применить к вычислению массы или моментов всей пластинки, занимающей конечную часть плоскости, так как есть неоднородность или по плотности  или по расстояниям
или по расстояниям 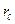 и
и  для различных точек пластинки.
для различных точек пластинки.
В соответствии с методикой приложения интегрального исчисления, разбиваем область D, занятую пластинкой, на малые (элементарные) части и составляем формулу для элементарного слагаемого искомой характеристики (Рис. 11), используя физические упрощения (например, можно считать каждую элементарную часть однородной или заменить её точечной массой). Затем суммируем все элементарные слагаемые и переходим к пределу при условии, что все элементарные части неограниченно измельчаются, убирая этим погрешность, допущенную при составлении элементарных слагаемых. В результате выходим на определение двойного интеграла по области D от некоторой функции координат x, y:
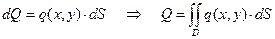 ,
,
где 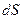 - это элементарная площадь
- это элементарная площадь
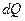 - это элементарное слагаемое величины
- это элементарное слагаемое величины  , аддитивной по области D.
, аддитивной по области D.
Формула для вычисления массы неоднородной пластинки имеющей поверхностную плотность  :
:
каждую элементарную часть пластинки считаем однородной, тогда

| (4) |
Формула для вычисления статических моментов тонких пластинок относительно координатных осей:
считаем каждую элементарную часть точечной массой; тогда
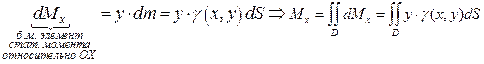
| (5) |
 Статический момент пластинки относительно оси Oy Статический момент тонкой пластинки относительно оси Ox Статический момент пластинки относительно оси Oy Статический момент тонкой пластинки относительно оси Ox
| (6) |
Формулы для вычисления моментов инерции тонких пластинок относительно координатных осей :
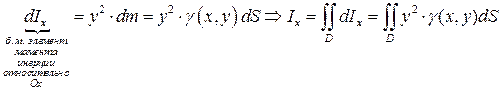
| (7) |

| (8) |
Формула для вычислеия момента инерции пластинки относительно точки начала координат:

| (9) |
Примеры 3 (вычисление механических характеристик тонких пластинок)
| 1. | Вычислить массу тонкого кольца, занимающего область D: 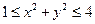 , если поверхностная плотность материала в точке , если поверхностная плотность материала в точке 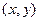 обратно пропорциональна квадрату расстояния от этой точки до начала координат и в точке обратно пропорциональна квадрату расстояния от этой точки до начала координат и в точке 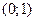 равна 1. равна 1.
|
Решение
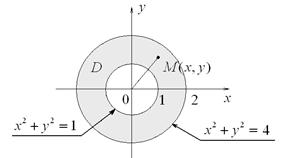
| Составляем формулу для плотности:
 , ,
 -коэффициент пропорциональности -коэффициент пропорциональности
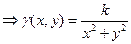 , так как , так как  ;
если ;
если 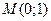 , то , то 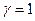 , то , то  ;
окончательно получаем, что ;
окончательно получаем, что
 . .
|
Составляем формулу для массы кольца аналогично тому, как была составлена формула (4):
 .
.
Теперь вычисляем двойной интеграл в полярных координатах:
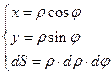

 ,
, 

Ответ: 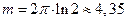 (единиц массы).
(единиц массы).
| 2. | Вычислить момент инерции I однородного квадрата со стороной a относительно его вершины. |
Решение
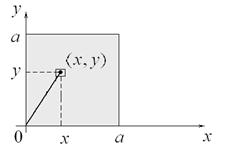
| Поместив квадрат в систему XOY, составляем формулу для искомого момента инерции: 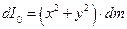 , где , где 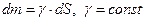  
|
Теперь вычисляем двойной интеграл в декартовых координатах, записав область D неравенствами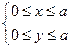 и учитывая, что
и учитывая, что 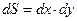 :
:
 Ответ:
Ответ: 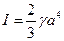 (единиц момента инерции).
(единиц момента инерции).
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 1123; Нарушение авторских прав?; Мы поможем в написании вашей работы!