
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ТЕМА II. Криволинейные и поверхностные интегралы
|
|
|
|
Приложения тройных интегралов
Приложения тройных интегралов аналогичны приложениям двойных интегралов, но только для трехмерных тел.
Если использовать одно из свойств тройного интеграла (о его значении от функции, тождественно равной единице), то получается формула для вычисления объема любого пространственного тела:
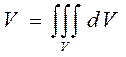
| (12) |
Объем пространственного тела
Пример 5 (вычисление объема с помощью тройного интеграла)
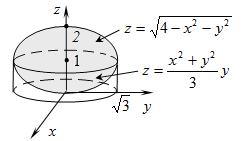
Найти объем тела, ограниченного поверхностями x 2 + y 2 + z 2 = 4 и x 2 + y 2 = 3 z.
| Решение
Находим линию пересечения поверхностей: 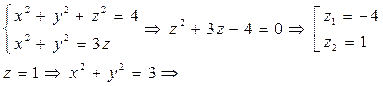 поверхности пересекаются по окружности радиуса
поверхности пересекаются по окружности радиуса 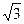 , лежащей в плоскости , лежащей в плоскости 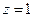 , параллельной XOY. , параллельной XOY.
|
Записываем формулу для объема через тройной интеграл и вычисляем тройной интеграл в цилиндрических координатах:

Ответ: 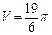 (единиц объема).
(единиц объема).
Формула для вычисления массы трехмерного объекта, занимающего объем V, имеет вид:
 (13)
(13)
Здесь  - это объемная плотность распределения массы.
- это объемная плотность распределения массы.
Пример 6 (вычисление массы трехмерного тела)
Найти массу шара радиуса R, если плотность пропорциональна кубу расстояния от центра и на единице расстояния равна k.
Решение
|
 :
:
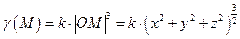 .
Теперь составим формулу (13) для массы шара: .
Теперь составим формулу (13) для массы шара:
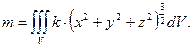 Этот тройной интеграл удобно вычислить в сферических координатах, записав в них систему неравенств для области шара:
Этот тройной интеграл удобно вычислить в сферических координатах, записав в них систему неравенств для области шара:
|

|
V: 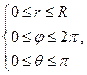 элементарный объем
элементарный объем 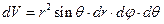 и
и 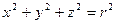 .
.
Тогда
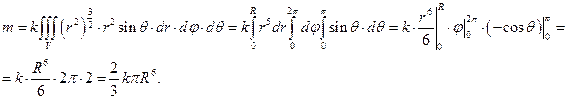
Заметим, что здесь при вычислении трехкратного интеграла получилось произведение интегралов, так как внутренние интегралы оказались не зависящими от переменных внешних интегралов.
Ответ: 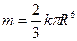 (единиц массы).
(единиц массы).
Механические характеристики для объема V (статические моменты, моменты инерции, координаты центра масс) вычисляются по формулам, которые
составляются по аналогии с формулами для двумерных тел.
| Объём V разбивается на малые элементарные части. Для каждой элементарной части составляется механическая характеристика как для материальной точки (x; y; z), имеющей массу dm. | 
|
Элементарные статические моменты и моменты инерции относительно координатных осей:

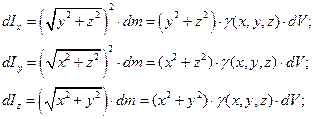
элементарные моменты инерции относительно координатных плоскостей и точки начала координат:

Далее, чтобы вычислить механическую характеристику всего объёма V,нужно просуммировать элементарные слагаемые этой характеристики по всем частям разбиения (так как вычисляемая характеристика обладает свойством аддитивности), а затем перейти к пределу в получившейся сумме при условии, что неограниченно уменьшаются (стягиваются в точки) все элементарные части разбиения. Эти действия описываются как интегрирование элементарного слагаемого вычисляемой механической характеристики по объёму V.
В результате получаются следующие формулы для вычисления статических моментов М и моментов инерции I трехмерных тел:
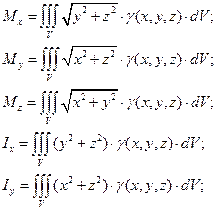
| 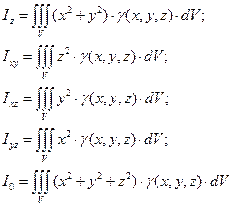
| (14) |
Формулы для координат центра масс трехмерного тела:
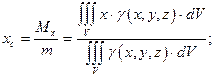 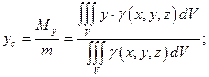 
| (15) |
На практике полезно эти формулы не только использовать как готовые, но и выводить их в решаемой задаче.
Примеры 7 (вычисление механических характеристик трехмерных тел)
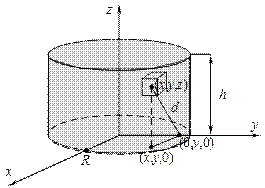
Найти момент инерции однородного цилиндра, высота которого h и радиус основания R, относительно оси, совпадающей с диаметром основания.
Решение
Если цилиндр поместить в систему координат, как указано на чертеже, то момент инерции будет находиться относительно оси OY.
Из физики известно, что момент инерции материальной точки вычисляется как квадрат расстояния от оси до этой точки, умноженный на массу:
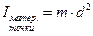
| 
|
Найдём расстояние d для произвольной точки цилиндра:
расстояние от точки с координатами 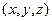 до оси
до оси 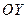 – это есть длина перпендикуляра, проведенного от этой точки к оси
– это есть длина перпендикуляра, проведенного от этой точки к оси 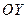 . Построим плоскость перпендикулярную оси
. Построим плоскость перпендикулярную оси 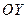 так, что точка
так, что точка 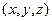 принадлежит этой плоскости. Тогда любая прямая, пересекающая ось
принадлежит этой плоскости. Тогда любая прямая, пересекающая ось 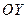 и принадлежащая этой плоскости, будет перпендикулярна
и принадлежащая этой плоскости, будет перпендикулярна 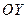 . В частности, прямая, соединяющая точку
. В частности, прямая, соединяющая точку 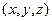 и точку
и точку 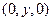 , будет перпендикулярна оси
, будет перпендикулярна оси 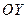 , а расстояние между этими точками и будет искомым расстоянием d. Вычисляем его по известной формуле расстояния между двумя точками:
, а расстояние между этими точками и будет искомым расстоянием d. Вычисляем его по известной формуле расстояния между двумя точками:
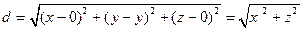
Теперь составляем бесконечно малый элемент искомого момента инерции относительно оси 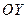 :
:
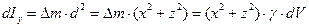 ,
,
в данной задаче 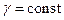 , так как цилиндр является однородным по условию.
, так как цилиндр является однородным по условию.
Интегрированием элементарного слагаемого 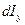 по объему цилиндра V получаем искомую механическую характеристику этого объема:
по объему цилиндра V получаем искомую механическую характеристику этого объема:
 .
.
Вычисляем составленный тройной интеграл в цилиндрических координатах:
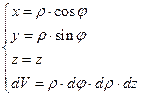
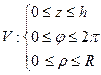
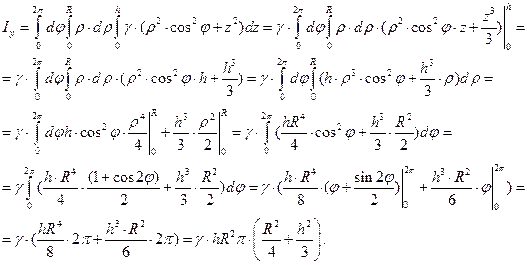
Ответ: 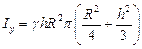 (единиц момента инерции).
(единиц момента инерции).
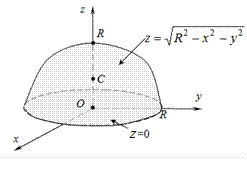
2. Определить координаты центра масс верхней половины шара радиуса R с центром в начале координат, считая плотность его материала постоянной.
Решение
Полушар ограничен поверхностями 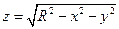 и и 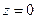 .
Так как полушар имеет имеет является однородным и ось симметрии .
Так как полушар имеет имеет является однородным и ось симметрии 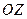 , то его центр масс лежит на этой оси. Поэтому , то его центр масс лежит на этой оси. Поэтому
 , , 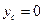 , , 
| 
|
Выносим в обоих тройных интегралах постоянную плотность 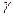 и переводим их в сферические координаты, заменяя
и переводим их в сферические координаты, заменяя 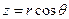 и
и 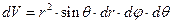 . В результате вычисления тройного интеграла получаем, что
. В результате вычисления тройного интеграла получаем, что

Ответ: 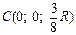 .
.
§5. Криволинейные интегралы I рода: определение, основные свойства, вычисление, некоторые приложения
Содержание
5.1. Определение криволинейного интеграла I рода. 42
5.2. Основные свойства криволинейного интеграла I рода. 44
5.3. Вычисление криволинейного интеграла I рода (Как вычисляется криволинейный интеграл I рода) 44
5.4. Некоторые приложения криволинейного интеграла I рода. 47
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 2783; Нарушение авторских прав?; Мы поможем в написании вашей работы!