Основные свойства криволинейного интеграла II рода

Свойство 1 (линейность криволинейного интеграла II рода по подынтегральному выражению)

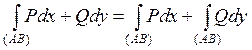
Свойство 2 (аддитивность криволинейного интеграла II рода по линии интегрирования)

, где точка С – это любая точка на линии (АВ).

Свойство 3 (зависимость криволинейного интеграла II рода от направления на линии интегрирования)

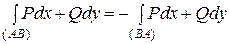
w Действительно, при изменении направления на дуге (АВ) проекции вектора 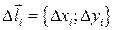изменят свои знаки, следовательно, изменит знак интегральная сумма и её предел (3). v

Свойство 4 (достаточное условие существования криволинейного интеграла II рода)

Если функции и 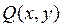являются непрерывными в каждой точке линии (AB), то существует

6.4. Вычисление криволинейного интеграла II рода в двумерном случае (Как вычисляется криволинейный интеграл II рода?)

Пусть линия (AB) задана параметрически: ,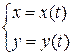

причем x (t) и y (t) — непрерывные и дифференцируемые функции,

t_A, t_B — это значения параметра t для начала и конца линии (AB).

Рассмотрим криволинейный интеграл (4) от одного слагаемого: (6)
В каждом слагаемом интегральной суммы можно сделать преобразования по теореме Лагранжа для дифференцируемой функции одной переменной: ,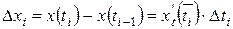

где 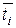— это фиксированное значение аргумента t из промежутка между точками t_{i -1} и t_i;

при этом D x_i ®0 означает, что D t_i ®0 вследствие непрерывности функции x (t).

Выберем 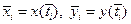, что всегда возможно, так как можно выбирать произвольно на каждой части разбиения.

Если учесть, что 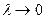в определении (6) означает, что 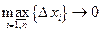, то формула (6) преобразуется к следующему виду:

.

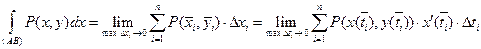Получился предел интегральной суммы для определенного интеграла по переменной 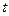изменяется от значения до значения , от функции, поэтому криволинейный интеграл (6) сводится к определенному интегралу по переменной t:

Аналогично: .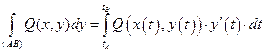

Если сложить оба результата, то получится формула сведения криволинейного интеграла II рода к определенному интегралу:

Формула сведения криволинейного интеграла II рода к определенному интегралу (7)
где t_A, t_B — это значения параметра t для начала и конца линии (AB).

Аналогичная формула составляется и для трехмерного криволинейного интеграла (1) по пространственной кривой (AB):

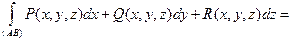
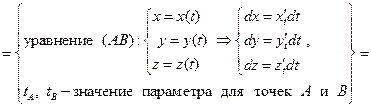
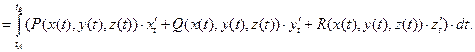
(8)

Таким образом, вычисление криволинейного интеграла II рода сводится к вычислению определенного интеграла по параметру, через который записаны уравнения линии интегрирования (АВ). При этом в качестве параметра можно взять любую независимую переменную на линии (АВ), а далее нужно выражать всё подынтегральное выражение в криволинейном интеграле через эту независимую переменную (параметр) и её дифференциал.

Дата добавления: 2014-10-15