Замечание. Если в двумерном случае дуга (AB) задана уравнением y = y(x), то в качестве независимой переменной (параметра) может быть взята переменная x

Если в двумерном случае дуга (AB) задана уравнением y = y(x), то в качестве независимой переменной (параметра) может быть взята переменная x, и формула (7) в этом случае примет следующий вид

(7^')
Если же дуга (АВ) задана уравнением x = x (y), то в качестве независимой переменной (параметра) может быть взята переменная y, и тогда сведение криволинейного интеграла к определенному интегралу по y описывается следующей формулой:

(7^'')

Примеры 1 (вычисление криволинейных интегралов II рода)

1. Вычислить , где (AB) — это верхняя полуокружность радиуса R, проходимая против часовой стрелки.

Решение

2. Вычислить , где (OA) — это дуга параболы y = x ^2 от точки O (0;0) до A (1;1). Решение

На линии (OA) можно в качестве параметра взять независимую переменную x и пересчитать все подынтегральное выражение через x и ее дифференциал dx:

Теперь сводим криволинейный интеграл к определенному интегралу по переменной x:

.

3. Вычислить , где (АВ) – это дуга линии , , .

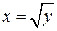Решение

На линии (АВ) возьмем в качестве независимой переменной и вычислим данный криволинейный интеграл по формуле (7"):

Отрицательное значение работы можно объяснить так: под действием данной силы 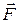перемещение материальной точки должно совершаться из точки 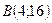в точку ; поэтому вычисленное значение - это значение работы, которую нужно затратить против силы .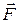

Ответ: (единиц работы).

Примеры 2 (вычисление работы переменной силы на криволинейном перемещении)

1. Вычислить работу, производимую силой при перемещении материальной точки вдоль дуги кривой 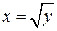из положения 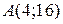в положение .

Решение

По физической трактовке криволинейного интеграла II рода составляем формулу для искомой работы ;

2. Сила по величине обратно пропорциональна расстоянию точки ее приложения от оси OZ, перпендикулярна к этой оси и направлена к ней. Найти работу силы при движении точки под действием этой силы по окружности 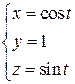от точки до точки .

Решение

Сделаем несколько иллюстраций к условию задачи:

;

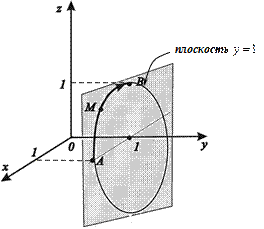
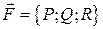, так как

,

так как , - коэффициент пропорциональности.

Вычисляем искомую работу с помощью криволинейного интеграла II рода:

Ответ: (единиц работы).

Дата добавления: 2014-10-15