Понятие факториала

Произведение n натуральных чисел от 1 до n обозначается сокращенно n!, то есть 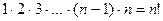(читается: n факториал).

Например, .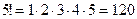

Считается, что 0! = 1.

Используя понятие факториала, формулу (1.1) можно представить так:

,

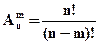(1.2)

где .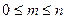

Очевидно, что 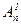= n (при m=1) и 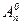= 1 (при m=0).

Пример 1.1. Правление коммерческого банка выбирает из 10 кандидатов трех человек на различные должности (все 10 кандидатов имеют равные шансы). Сколько всевозможных групп состоящих из трех человек, можно составить из 10 кандидатов?

Решение. В условии задачи речь идет о расчете числа комбинаций из 10 элементов по 3. Так как группы по 3 человека могут отличаться и составом претендентов, и заполняемыми ими вакансиями, т.е. порядком, то для ответа на пункт а) необходимо рассчитать число размещений из 10 элементов по 3.

.

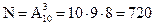Ответ. Из 10 человек можно составить 720 различных групп, состоящих из трех человек.

Дата добавления: 2014-10-22