Числовые характеристики ДСВ

1. Математическим ожиданием дискретной случайной величины называется сумма вида

М(Х)=х₁р₁ + х₂р₂ + … +х_np_n

где х_i – возможные значения дискретной случайной величины; p_i – вероятность появления значения х_i.

Замечание 1. Из определения следует, что М(Х)=const.

Замечание 2. Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.

Вероятностный смысл. Математическое ожидание приблизительно равно среднему арифметическому наблюдаемых значений случайной величины (тем точнее, чем больше испытаний).

Свойства математического ожидания:

1. М(СХ) = С×М(Х); М(С) = С, где С – произвольная постоянная величина.

2. М(Х₁ × Х₂ ××× Х_n) = M(X₁)×M(X₂) ××× M(X_n), если Х₁, Х₂, …, Х_n – взаимно независимые случайные величины.

3. М(Х₁ + Х₂ + ××× + Х_n) = M(X₁) + M(X₂) + ××× + M(X_n).

4. Если Х – дискретная случайная величина с биномиальным законом распределения, то М(Х) = np, где n – число испытаний, р – вероятность появления в одном испытании.

2. Рассеяние случайной величины около среднего значения характеризуют дисперсия и среднее квадратическое отклонение, т.к. математическое ожидание не дает полной картины.

Определение 1. Оклонением называется разность между отклонением случайной величины и ее математическим ожиданием.

Теорема1. Математическое ожидание отклонения равно нулю: М(Х-М(Х))=0.

Доказательство. М(Х – М(Х)) = М(Х) – М(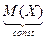) = М(Х) – М(Х) = 0, ч.т.д.

Замечание. Вычислив возможные значения отклонения и найдя их среднее ничего не получим, т.к. их среднее равно нулю (по теореме1), поэтому чаще вычисляют среднее значение квадрата отклонения.

Определение 2. Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X) = M(X – M(X))²

Замечание: используя свойства математического ожидания, можно получить более простую для вычисления дисперсии формулу.

Теорема2. Дисперсия равна разности между математическим значением случайной величины и квадратом ее математического ожидания:

D(X) = M(X²) – [M(X)]²

Доказательство.

D(X) = M(X² – 2M(X)X + (M(X))²) = М(Х²) – 2М(ХМ(Х)) + М=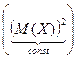

= М(Х²) – 2М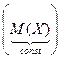М(Х) + 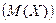² = М(Х²) – 2М(Х)×М(Х) + =

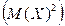= М(Х²) - .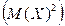

Свойства дисперсии:

1. D(СХ) = С²×D(Х); D(С) = 0, где С – произвольная постоянная величина.

2. D(Х₁ + Х₂ + ××× + Х_n) = D(X₁) + D(X₂) + ××× + D(X_n), где Х₁, Х₂, …, Х_n – взаимно независимые случайные величины.

Следствие. D(Х – У) = D(X) + D(Y).

3. Если Х – дискретная случайная величина с биномиальным законом распределения, то D(Х) = npq, где n – число испытаний, р – вероятность появления, а q – вероятность непоявления в одном испытании.

3. Средним квадратическим отклонением дискретной случайной величины Х называется число s(Х) = .

Применяют в тех случаях, когда необходимо, чтобы оценка рассеивания имела размерность случайной величины.

Дата добавления: 2014-10-22