Основные понятия и определения

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Современная статистика разрабатывает планирование эксперимента, занимается последующим анализом и др.

Если требуется изучить совокупность однородных объектов относительно некоторого признака, то на практике не изучают каждый элемент, а случайно отбирают ограниченное число объектов и изучают их.

Выборкой называют совокупность случайно отобранных объектов.

Генеральной называется совокупность объектов, из которых производится выборка.

Объем совокупности – это число объектов этой совокупности.

Наиболее удобно выборку записывать в виде таблицы:

х1	х2	…	xk
n1	n2	…	nk

где наблюдаемые значения х_i называются вариантами (каждое из х_i наблюдалось n_i раз), а указанная последовательность вариант, записанных в возрастающем порядке называется вариационным рядом, n_i – частоты.

Выборочной средней 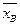называется среднее арифметическое значение признака выборки

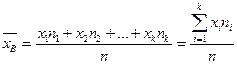
где n=n₁ + n₂ +…+n_k – объем выборки.

Выборочной дисперсией D_В называется среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения :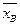

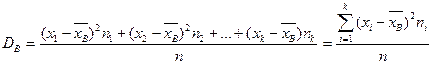
n – объем выборки.

Выборочное среднее квадратическое отклонение: s_В = .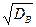

Аналогично теории вероятностей справедлива теорема о формуле для подсчета дисперсии:

Теорема: D_B=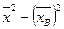, где 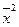вычисляют по формуле: .

Доверительным называют интервал (Q^*-d; Q^*+d), который покрывает неизвестный параметр с заданной надежностью g. (Здесь: Q^* - статистическая характеристика неизвестного параметра Q, d - точность оценки, а надежность оценки g - это вероятность, с которой осуществляется неравенство | Q – Q^*| < d.

С помощью формул теории вероятностей (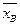рассматривают как случайную величину 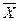) можно доказать, что с надежностью g доверительный интервал 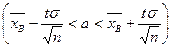покрывает неизвестный параметр а (математического ожидания нормального распределения) при известном s, где точность оценки 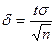; n – объем выборки; t определяют из равенства Ф(t)=(по таблице приложения 2 находят аргумент t, которому соответствует значение функции Лапласа, равное g/2).

Замечание. Если же s неизвестно, то доверительный интервал, покрывающий неизвестный параметр а с надежностью g, примет вид: 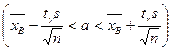, где t_g можно определить по таблице приложения 3 по заданным n и g, s = 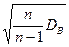- «исправленное» среднее квадратическое отклонение (нетрудно видеть, что при n ³ 30 s и s_В практически совпадают).

Пример 32. Дана выборка объема n=10:

хi	-2
ni

Оценить с надежностью 0,95 математическое ожидание а нормально распределенного признака по выборочной средней при помощи доверительного интервала.

Решение: вычислим по определению выборочную среднюю

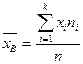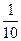= (-2×2 + 1×1 + 2×2 + 3×2 + 4×2 + 5×1) = 2;

D_В = 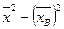= 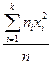- 2² = 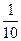[(-2)²×2 + 1²×1 + 2²×2 + 3²×2 + 4²×2 + 5²×1] – 4 = = 5,2 Þ s= 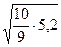» 2,4.

Пользуясь таблицей приложения 3 по g = 0,95 и n = 10, находим t_g=2,26, тогда искомый доверительный интервал 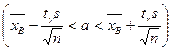примет вид: 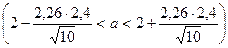, т.е. .

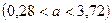Ответ: .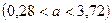

Дата добавления: 2014-10-22