
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Повторные испытания
|
|
|
|
ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА.
Теорема 1. Пусть событие А может произойти при условии появления одного из попарно несовместных событий Н1, Н2, …Нn, которые образуют полную группу, причем известны Р(Н1), P(H2), …, P(Hn) и Р(А/H1), P(A/H2), …, P(A/Hn), тогда вероятность события А равна
| Р(А) = Р(Н1)Р(А/H1) + P(H2)P(A/H2) + … + P(Hn)P(A/Hn) |
Эта формула называется формулой полной вероятности.
Доказательство. По условию А= АН1 + АН2 + … +АНn. Т.к. Н i – несовместные, то АН i – тоже несовместные (i =1, 2, …, n), следовательно, по теореме сложения Р(А) = Р(АH1) + P(AH2) + … + P(AHn). По теореме умножения P(AH i)=Р(А)Р(А/Н i), следовательно, Р(А) = Р(АH1) + P(AH2) + … + P(AHn)= =Р(Н1)Р(А/H1) + P(H2)P(A/H2) + … + P(Hn)P(A/Hn), ч.т.д.
Замечание. События Н i называют гипотезами, т.к. зарание неизвестно, которое из них наступит.
Если предположить, что в результате испытания событие А уже произошло, то возникает задача: вычислить условные вероятности появления гипотез, т.е. вычислить Р(H1/А), P(H2/A, …, P(Hn/A).
Теорема 2. Пусть событие А может произойти при условии появления одного из попарно несовместных событий Н1, Н2, …Нn, которые образуют полную группу, и пусть известно, что в результате испытания событие А произошло, тогда условная вероятность i -той гипотезы равна
Р(А/H i) = 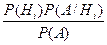
|
Эта формула называется формулой Байеса.
Замечание. Здесь Р(А) вычисляют по формуле полной вероятности.
Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна р (0<p<1), то вероятность того, что событие А появится в этих n испытаниях ровно k раз можно вычислить по формуле Бернулли:
Рn (k)=С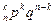
|
где q = 1 – p.
Например. Вероятность выиграть по лотерейному билету равна 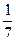 . Найти вероятность выиграть по двум билетам из пяти.
. Найти вероятность выиграть по двум билетам из пяти.
Решение: по условию р = 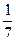 , значит q =
, значит q = 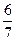 ; n = 5, k = 2. Тогда по формуле Бернулли получаем P5(2)=C
; n = 5, k = 2. Тогда по формуле Бернулли получаем P5(2)=C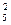
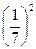
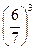 =
= 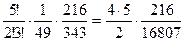 =0,1285.
=0,1285.
Ответ: 0,1285.
Замечание: если число испытаний n велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях пользуются предельными теоремами Лапласа.
Локальная теорема Лапласа дает асимптотическую формулу для приближенного вычисления вероятности появления в n испытаниях события А k раз, если n велико. В 1730г для р=0,5 асимптотическая формула была найдена Муавром, а в 1783г Лаплас обобщил формулу Муавра для произвольного р¹0 и ¹1 (поэтому локальную теорему Лапласа иногда называют теоремой Муавра-Лапласа)
Теорема1 (локальная теорема Лапласа).
Если вероятность р появления события А в каждом испытании постоянна и р¹0, р¹1, то вероятность того, что событие А появится в n испытаниях ровно k раз приблизительно равна значению функции 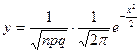 =
= 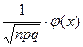 при х =
при х = 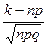 .
.
Замечание 1. Вероятность тем точнее, чем выше n.
Замечание 2. З начения функции 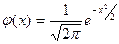 можно вычислять на калькуляторе или по таблицам (см. приложение 1). Причем, очевидно, функция j(х) – четная, т.е. j(−х) = j(х).
можно вычислять на калькуляторе или по таблицам (см. приложение 1). Причем, очевидно, функция j(х) – четная, т.е. j(−х) = j(х).
| Таким образом, | Pn(k)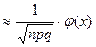 , где , где
| q = 1-p, х = 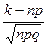 . .
|
Замечание 3. Иногда используют формулу Пуассона Pn(k)=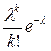 ,
,  .
.
Теорема2 (интегральная теорема Лапласа).
Если вероятность р наступления события А в каждом испытании постоянна и р ≠ 0, р ≠ 1, то вероятность Рn(k1< k < k2) того, что событие А появится в n испытаниях от k1 до k2 раз, приближенно равна Рn(k1≤ k ≤k2) ≈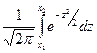 , где х1 =
, где х1 = 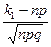 , х2 =
, х2 = 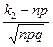 .
.
Рассмотрим для облегчения функцию Ф(х) = 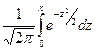 , ее называют функцией Лапласа, значения которой приведены в таблице, и преобразуем формулу из формулировки теоремы 2, чтобы ее было удобно применять:
, ее называют функцией Лапласа, значения которой приведены в таблице, и преобразуем формулу из формулировки теоремы 2, чтобы ее было удобно применять:
Рn(k1≤ k ≤k2) ≈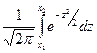 =
=  +
+  =
=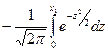 +
+
+ = – Ф(х1) + Ф(х2).
= – Ф(х1) + Ф(х2).
| Таким образом, | Рn(k1≤ k ≤k2) ≈ Ф(х2) – Ф(х1) | где х1 = 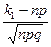 , х2 = , х2 = 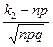
|
Замечание 4. Функция Ф(х) – нечетная, т.е. Ф(−х) = −Ф(х), и при всех х >5 можно принять Ф(х)=0,5.
Замечание 5. При малых n лучше вероятности считать по формуле Бернулли, и применять теорему сложения вероятностей.
Наивероятнейшее число появлений k 0 события А в n испытаниях можно определить из двойного неравенства:
np – q 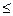 k0 k0 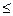 np + p np + p
|
где р – вероятность появления в одном испытании, q = 1 – р.
Здесь: 1) если np – q - дробное, то двойное неравенство имеет единственное целое решение; 2) если np – q - целое, то двойное неравенство имеет два целых решения.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 315; Нарушение авторских прав?; Мы поможем в написании вашей работы!