Разложение некоторых элементов функций

I. ;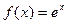

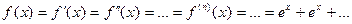
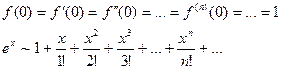
Вид остаточного члена:

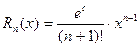, где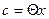

Докажем, что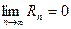

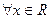
Учитывая:

1)

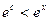
2) 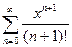, сходится 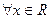(применим признак Даламбера, проверим)

получаем:

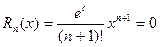
поэтому: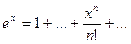

II.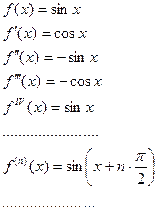

Полагая :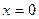

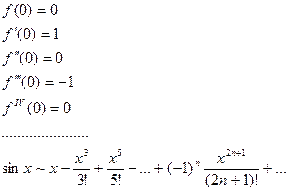
(2)

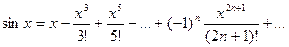
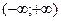
III. 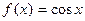дифференцируя ряд для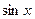, получим разлож. 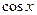в степенной ряд:

(3)

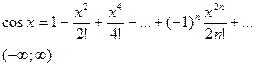
IV. Бинномеальный ряд.

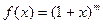, где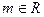

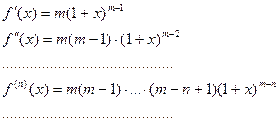
Получаем :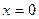

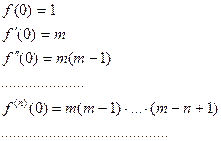
Ряд записывается в виде:

(4) 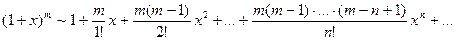область сходимости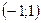

Замечание: если m – целое число, то ряд справа содержащий 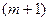слагаемых и обращается в формулу Бинома Ньютона.

V.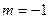

(5)

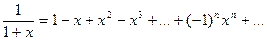
VI.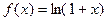

Применим теорему об интегрировании степенного ряда к ряду (5). Интегрировать в пределе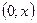

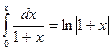
Почленно интегрируем правую часть:

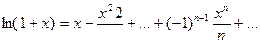(6)

Приложение степенных рядов.

Степенные ряды широко применяют в приближенных вычислениях:

1) для приближенных вычислений значений функций

2) для вычисления определённых интегралов

3) для приближенного интегрирования дифференциальных уравнений.

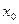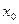Допустим, что известны значения самой функции и её последовательность производных в некоторой точке . И мы допустим, что функция в окрестности разлагается в ряд Тейлора (Маклорена), тогда точное значение функции в любой точке этой окрестности может быть вычислено по ряду Тейлора, а приближенное её значение по частичной сумме этого ряда.

Возникшую при этом ошибку можно оценить: 1) либо опираясь на теорему об оценке остаточного члена 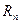. 2) либо непосредственно оценивая остаток ряда. Если например получающийся ряд знакочередующийся, то это делается при помощи теоремы Тейлора 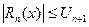, где 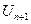- первый из отброшенных членов ряда.

Ошибка, которая по абсолютной величине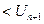

Например:1) Вычислить с точностью до Е=0,0001

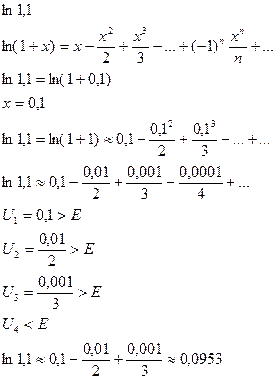
2) Вычисление Интеграла.

Разлагая подъинтегральную функцию в степенной ряд, можно, используя теорему об интегрировании степенных рядов, представить интеграл: 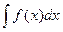в виде степенного ряда и подсчитать величину этого интеграла с заданной точностью при любом значении t из интервала сходимости этого ряда.

Например:

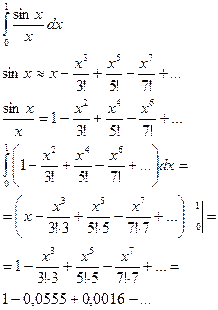
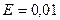
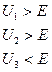
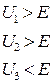
- его не берём

Ответ: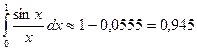

3) Вычисление дифференциального уравнения с помощью степенных рядов.

Пусть задано дифференциальное уравнение:

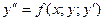
Предположим, что решение искомое есть 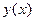разлагается в степенной ряд в окрестности точки 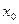. Нужно найти решение уравнения, удовлетворяющее начальным условиям.

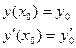
Причём функция 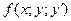в точке 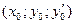имеет частные производные любого порядка, тогда коэффициенты ряда – решения:

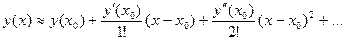
Коэффициенты определяются путём последовательного дифференцирования исходного уравнения и подстановки в него 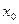и найд.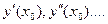

Например: Найти 3 первых члена, отличных от нуля, разложенные в степенной ряд частного решения дифференциального уравнения

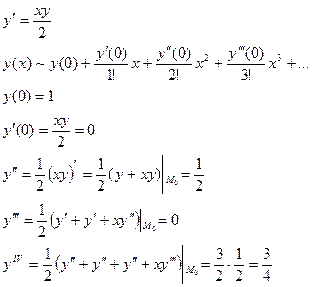
Ответ: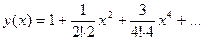

Дата добавления: 2014-10-22