ГЛОССАРИЙ. Таблица производных сложной функции

30..

Приложение 1

Таблица производных сложной функции

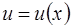
1.

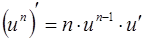
2.

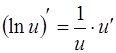
3.

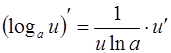
4.

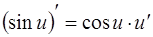
5.

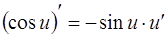
6.

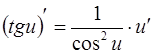
7.

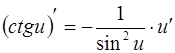
8.

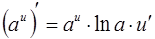
9.

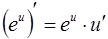
10.

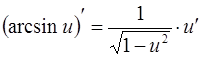
11.

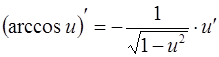
12.

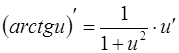
13.

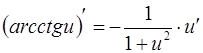
14.

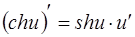
15.

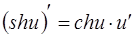
16.

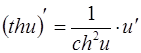
17.

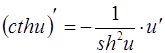
18. 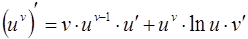, где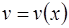

Приложение 2

Контрольная работа «Техника дифференцирования сложной функции»

Для проверки прочности навыка, приобретенного в ходе решения предыдущих задач, предлагаем варианты контрольной работы по теме "Дифференцирование сложных функций" с решениями.

Вариант 1
1. 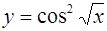;	5. ;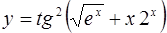
2. 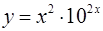;	6. ;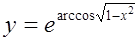
3. 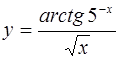;	7. ;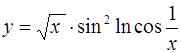
4. 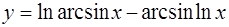;	8. .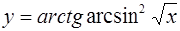

Вариант 2
1. 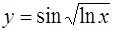;	5. ;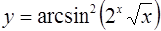
2. 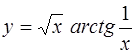;	6. ;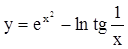
3. 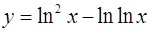;	7. ;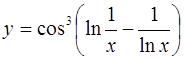
4. 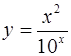;	8. .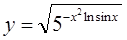

Вариант 3
1. 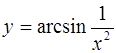;	5. ;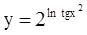
2. 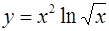;	6. ;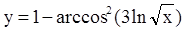
3. 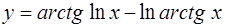;	7. ;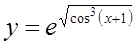
4. 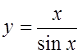;	8. .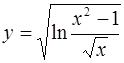

Вариант 4
1. 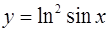;	5. ;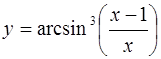
2. 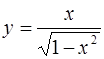;	6. ;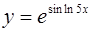
3. 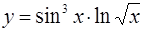;	7. ;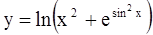
4. 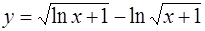;	8. .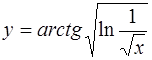

Вариант 5
1. 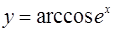;	5. ;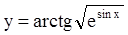
2. 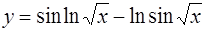;	6. ;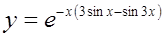
3. 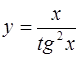;	7. ;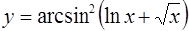
4. 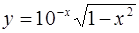;	8. .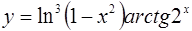

Вариант 6
1. 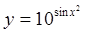;	5. ;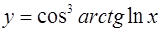
2. 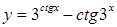;	6. ;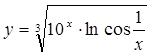
3. 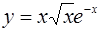;	7. ;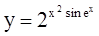
4. 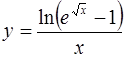;	8. .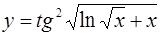

Ниже приводятся решения этих задач. Тождественные преобразования выполнены лишь в отдельных случаях, когда: либо запись существенно сокращается, либо нужно напомнить читателю, как следует записывать некоторые выражения.

Решения вариантов контрольной работы

Вариант 1

1. ;

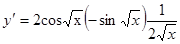2.

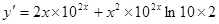
3. ;

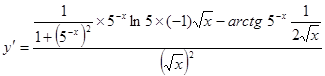4. ;

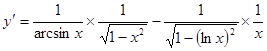5.

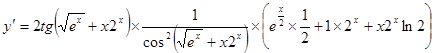
Указание: ;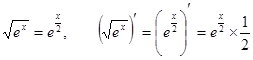

Или иначе: .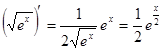

6.

.

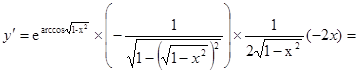
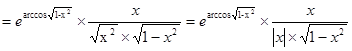7.

.

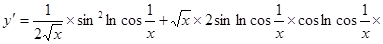
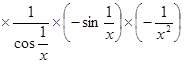8.

.

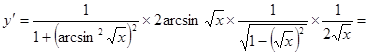
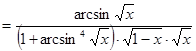Вариант 2

1. ;

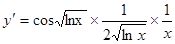2. ;

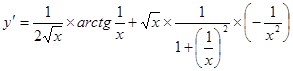3. ;

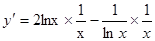4. ;

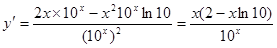5. ;

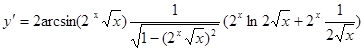6. ;

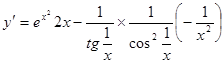7. .

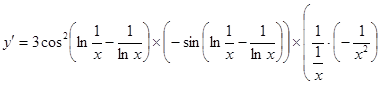
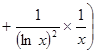Указание: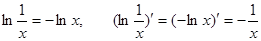

или: .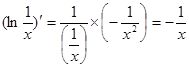

8. .

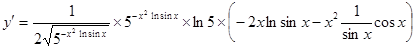Вариант 3

1. ;

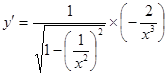Здесь: .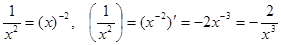

2. ;

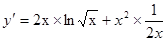Указание: ;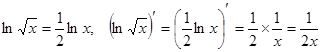

или ;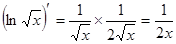

3. ;

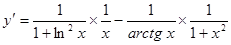4.;

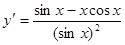5.;

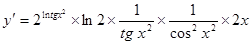6.;

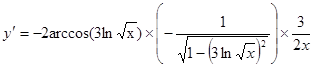7.

;

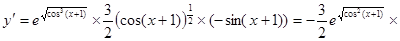
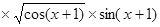Указание: .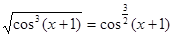

8.

;

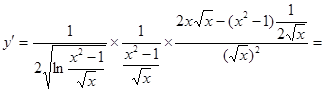
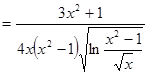или ,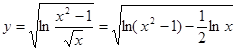

.

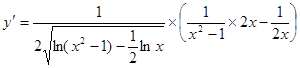Вариант 4

1. ;

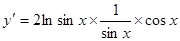2. ;

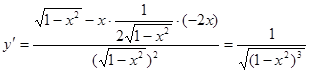3.;

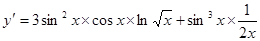Указание: ;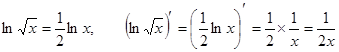

или ;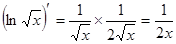

4.;

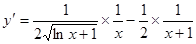Указание: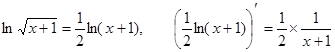

или .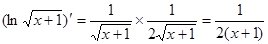

5.

;

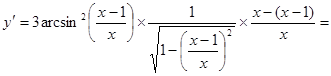
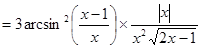6. ;

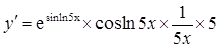7.;

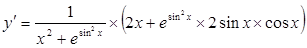8.;

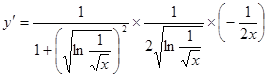Указание: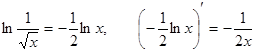

или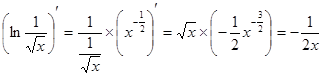

Вариант 5

1. ;

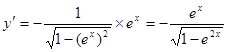2.;

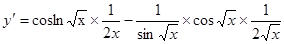3.;

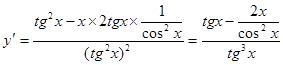4.;

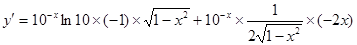5.

;

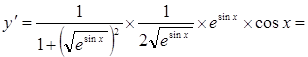
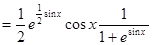6.;

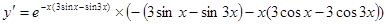7. ;

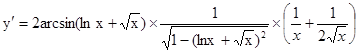8.

.

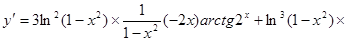
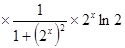Вариант 6

1. ;

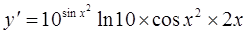2.;

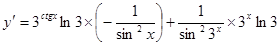3.;

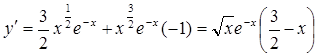Указание: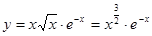

4. ;

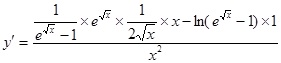5. ;

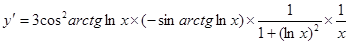6.;

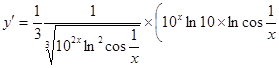
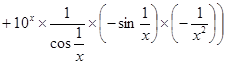7.;

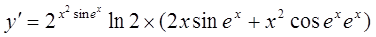8..

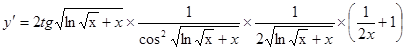Вектор касательной к кривой Г, заданной вектором 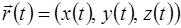- это вектор с координатами .

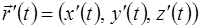Вектор- функция –это вектор 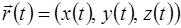, заданный на множестве М точек числовой прямой.

Геометрический смысл дифференциала: дифференциал функции равен приращению ординаты касательной к кривой 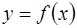в данной точке .

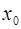Геометрический смысл производной: производная функции 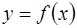при данном значении аргумента 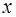- это тангенс угла, образованного касательной к графику функции в точке 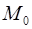с положительным направлением оси ОХ.

Годограф вектор- функции 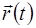- это геометрическое место концов векторов 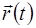, выходящих из нулевой точки О.

Дифференциал - это главная часть приращения функции.

Дифференциал n-го порядка от функции 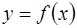- этодифференциал от дифференциала 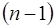порядка, т.е.

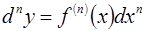
Дифференцирование - это операция вычисления производной.

Инвариантность формы дифференциала: форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента.

Касательная к графику функции 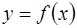в точке 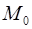- это предельное положение секущей 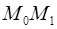при условии .

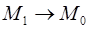Кривизна кривой- это длина скорости вращения единичного касательного вектора к кривой в данной точке относительно переменной длины дуги.

Правило Лопиталя для раскрытия неопределенносте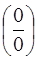й и 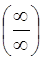: предел отношения функций равен пределу отношения производных.

Производная вектор- функции в точке t - это предел отношения приращения вектор – функции 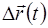к приращению аргумента 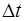, когда последнее стремится к нулю:

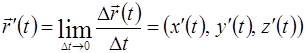
Производная n-го порядка - это производная от производной (n-1) –го порядка:

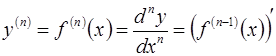
Производная от функции 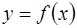в точке 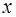- это предел отношения приращения функции к приращению аргумента, когда последнее стремиться к нулю:

.

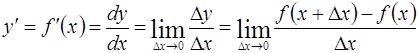Промежутки монотонности – это промежутки возрастания и убывания функции.

Физический смысл производной – это скорость изменения функции.

Физический смысл производной второго порядка – это ускорение прямолинейного движения в данный момент времени равно производной второго порядка от пути по времени, вычисленной для данного момента.

.

Дата добавления: 2014-10-22